HNSW算法详解

大家好，欢迎来到IT知识分享网。

目录

1. 数据结构

2. 添加节点

3. 更新节点

4. 搜索节点

4.1 第0层以上

4.2 第0层

5. 总结

文章略长，建议先收藏，慢慢品~

基于图的向量检索算法在向量检索的评测中性能都是比较优异的。如果比较在乎检索算法的效率，而且可以容忍一定的空间成本，多数场景下比较推荐基于图的检索算法。而HNSW是一种典型的，应用广泛的图算法，很多分布式检索引擎都对HNSW算法进行了分布式改造，以应用于高并发，大数据量的线上查询。本文将结合hnswlib的源码，对HNSW算法进行详细的阐述。

1. 数据结构

HNSW将空间中的向量按上图的形式组织，每一个节点插入时，首先将数据保存在第0层。然后随机一个层数，从该层开始逐层往下遍历，每层都将该节点(以节点内部id代表)插入，并按一定规则(后文介绍)连接M个近邻节点，直至第0层。

HNSW主要用到了两块内存来表示如上图所示的结构。data_level0_memory_以及linkLists_。两者的内部结构如下图所示：

data_level0_memory_存储节点的数据以及第0层的邻居关系，每个节点的数据主要包括：邻居的数量(size)，flag，保留的一个字节，邻居节点的id，自己的data数据，以及一个label(插入节点时可指定的一个代号)。

linkLists_是一个二维数组，其中的每一行代表一个节点从第1层到maxLevel层每一层的邻居关系。每个节点每一层的数据结构主要包括：邻居的数量(size)，保留的两个字节，以及该层的邻居的id。

具体的结构代码如下：

size_links_level0_ = maxM0_ * sizeof(tableint) + sizeof(linklistsizeint); //jeven: size of graph link of each element in level 0 size_data_per_element_ = size_links_level0_ + data_size_ + sizeof(labeltype); //jeven: size of each element offsetData_ = size_links_level0_; label_offset_ = size_links_level0_ + data_size_; offsetLevel0_ = 0; data_level0_memory_ = (char *) malloc(max_elements_ * size_data_per_element_); // jeven: total memory of level 0 if (data_level0_memory_ == nullptr) throw std::runtime_error("Not enough memory"); linkLists_ = (char ) malloc(sizeof(void *) * max_elements_); if (linkLists_ == nullptr) throw std::runtime_error("Not enough memory: HierarchicalNSW failed to allocate linklists"); size_links_per_element_ = maxM_ * sizeof(tableint) + sizeof(linklistsizeint);

2. 添加节点

添加节点时，先检查一下该节点的label是否已经存在了，如果存在的话，直接更新节点，下一节会详细介绍。如果不存在，则直接添加节点。主要步骤为：

1. 节点id自增加1
2. 随机初始化层数 curlevel
3. 初始化节点相关数据结构，主要包括：将节点数据以及label拷贝到第0层数据结构(data_level0_memory_)中；为该节点分配存储0层以上的邻居关系的结构，并将其地址存储在linkLists_中
4. 如果这是第一个元素，只需将该节点作为HNSW的entrypoint，并将该元素的层数作为当前的最大层。
5. 如果不是第一个元素：1）那么从当前图的从最高层逐层往下寻找直至节点的层数+1停止，寻找到离data_point最近的节点，作为下面一层寻找的起始点。2）从curlevel依次开始往下，每一层寻找离data_point最接近的ef_construction_（构建HNSW是可指定）个节点构成候选集，再从候选集中选择M个节点与data_point相互连接。至于如何寻找ef_construction_个候选节点，在后文搜索节点一节中解释。

主要代码如下，注释中均按上面相应的步骤注明：

 // jeven: 1. 节点编号id自增，为cur_c cur_c = cur_element_count; cur_element_count++; label_lookup_[label] = cur_c; // jeven: 2. 随机初始化层数 int curlevel = getRandomLevel(mult_); element_levels_[cur_c] = curlevel; // jeven: 3. 初始化节点相关数据结构 memset(data_level0_memory_ + cur_c * size_data_per_element_ + offsetLevel0_, 0, size_data_per_element_); memcpy(getExternalLabeLp(cur_c), &label, sizeof(labeltype)); memcpy(getDataByInternalId(cur_c), data_point, data_size_); if (curlevel) { linkLists_[cur_c] = (char *) malloc(size_links_per_element_ * curlevel + 1); if (linkLists_[cur_c] == nullptr) throw std::runtime_error("Not enough memory: addPoint failed to allocate linklist"); memset(linkLists_[cur_c], 0, size_links_per_element_ * curlevel + 1); } // jeven: 5.待添加的节点不是第一个元素 if ((signed)currObj != -1) { if (curlevel < maxlevelcopy) { dist_t curdist = fstdistfunc_(data_point, getDataByInternalId(currObj), dist_func_param_); for (int level = maxlevelcopy; level > curlevel; level--) { // jeven: 5.1 逐层往下寻找直至curlevel+1，找到最近的节点 ...... } } // jeven: 5.2 从curlevel往下，找一定数量的邻居并连接 for (int level = std::min(curlevel, maxlevelcopy); level >= 0; level--) { std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> top_candidates = searchBaseLayer(currObj, data_point, level); currObj = mutuallyConnectNewElement(data_point, cur_c, top_candidates, level, false); // jeven: 连接节点与邻居 } } else { // jeven: 4. 只需更新起始点和最大层 // Do nothing for the first element enterpoint_node_ = 0; maxlevel_ = curlevel; }

这里值得注意的一点是 ：若候选集(top_candidates)中节点的数量大于M时，如何从中选择M个节点与data_point相连。首先容易想到的是从候选集中选择最近的M个点。这样有一个问题，就是容易形成孤岛。如下图所示，a点为将要插入的点。假设M为2，如果找寻最近的2个黑色的点与之相连，则黑色的点肯定在cluster1中，这样就造成cluster1与cluster2分裂，最终构成的图也不是连通图，会影响搜索结果。

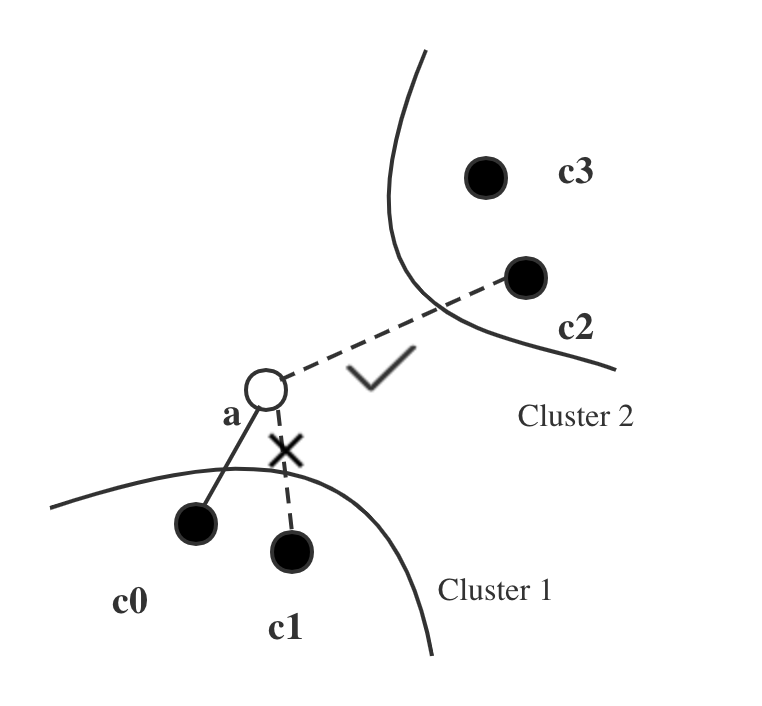
为了防止cluster分裂，hnswlib采用一种叫启发式搜索的方法。每选择一个节点时，都要看此节点到目标节点a的距离是否比此节点到所有已选中的节点远，如果远，则选中它。上图中先选c0，计算c1时，因为它距离c0比距离a近，所以可能c0和c1属于一个集群，故不选它，而选择c2。 现假设c0~c3都在候选集中，从中选择两个节点相连。详细步骤如下：

1. 先将c0~c3按照到a点的距离从近到远排序，为c0, c1,c2,c3，放在队列queue中。
2. 从队列中依次取出一个节点，第一次取c0,将c0选为a的邻居，先存在return_list中。
3. 再从队列中取出下一个节点c1，计算出c1到a点的距离d1。依次计算return_list中已选中的所有节点(也就是c0)到a点的距离，并与d1相比较，发现c0和c1更近，因此不选c1
4. 在从队列中取出一个节点c2，计算出c2到a点的距离d2。依次计算return_list中已选中的所有节点(也就是c0)到a点的距离，并与d2相比较，发现c0和c2更远，选中c2
5. 至此，return_list的size为2，结束筛选。

代码如下：

 void getNeighborsByHeuristic2(std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> &top_candidates, const size_t M) { if (top_candidates.size() < M) { return; } // jeven:入队列 std::priority_queue<std::pair<dist_t, tableint>> queue_closest; std::vector<std::pair<dist_t, tableint>> return_list; while (top_candidates.size() > 0) { queue_closest.emplace(-top_candidates.top().first, top_candidates.top().second); top_candidates.pop(); } while (queue_closest.size()) { if (return_list.size() >= M) break; std::pair<dist_t, tableint> curent_pair = queue_closest.top(); dist_t dist_to_query = -curent_pair.first; //jeven: distance between new point and current point queue_closest.pop(); bool good = true; // jeven: compare with distances of selected points to current point for (std::pair<dist_t, tableint> second_pair : return_list) { dist_t curdist = fstdistfunc_(getDataByInternalId(second_pair.second), getDataByInternalId(curent_pair.second), dist_func_param_);; if (curdist < dist_to_query) { // jeven: 如果当前节点到某一个已选中的节点比到新增节点近，则淘汰掉 good = false; break; } } if (good) { return_list.push_back(curent_pair); } } for (std::pair<dist_t, tableint> curent_pair : return_list) { top_candidates.emplace(-curent_pair.first, curent_pair.second); } }

3. 更新节点

上一节提到，插入节点时，如果节点的label已经存在了，那么直接更新节点。更新节点主要分为三步：

1. 更新节点的数据；
2. 从0层逐层往上，直至该节点的最高层，在每一层取待更新节点的部分邻居，更新它们的邻居；
3. 从上往下依次更新待更新节点的邻居。

第一步很简单，直接把数据拷贝到0层相应的位置即可：

memcpy(getDataByInternalId(internalId), dataPoint, data_size_);

 第二步，更新原来的部分邻居的邻居。

 std::unordered_set<tableint> sCand; std::unordered_set<tableint> sNeigh; // jeven: store part of original neighbors need to be updated std::vector<tableint> listOneHop = getConnectionsWithLock(internalId, layer); // jeven: get original neighbors if (listOneHop.size() == 0) continue; sCand.insert(internalId); for (auto&& elOneHop : listOneHop) { sCand.insert(elOneHop); // jeven: store nodes of one hop into sCand // jeven: choose part of neighbors to update, updateNeighborProbability belongs to [0,1.0], if updateNeighborProbability is 1.0, all neighbors will be updated if (distribution(update_probability_generator_) > updateNeighborProbability) continue; // jeven: store part(0~100%) of original one hops into sNeigh, and get two-hop of them into sCand sNeigh.insert(elOneHop); std::vector<tableint> listTwoHop = getConnectionsWithLock(elOneHop, layer); for (auto&& elTwoHop : listTwoHop) { sCand.insert(elTwoHop); } } // jeven: part of one-hops for (auto&& neigh : sNeigh) { // if (neigh == internalId) // continue; std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> candidates; size_t size = sCand.find(neigh) == sCand.end() ? sCand.size() : sCand.size() - 1; // sCand guaranteed to have size >= 1 size_t elementsToKeep = std::min(ef_construction_, size); for (auto&& cand : sCand) { if (cand == neigh) continue; dist_t distance = fstdistfunc_(getDataByInternalId(neigh), getDataByInternalId(cand), dist_func_param_); if (candidates.size() < elementsToKeep) { candidates.emplace(distance, cand); } else { if (distance < candidates.top().first) { candidates.pop(); candidates.emplace(distance, cand); } } } // Retrieve neighbours using heuristic and set connections. getNeighborsByHeuristic2(candidates, layer == 0 ? maxM0_ : maxM_); { std::unique_lock <std::mutex> lock(link_list_locks_[neigh]); linklistsizeint *ll_cur; ll_cur = get_linklist_at_level(neigh, layer); size_t candSize = candidates.size(); setListCount(ll_cur, candSize); tableint *data = (tableint *) (ll_cur + 1); for (size_t idx = 0; idx < candSize; idx++) { data[idx] = candidates.top().second; candidates.pop(); } } }

for循环遍历每一层，在for循环里面，首先挑部分原来的邻居，存储在 sNeigh里面， 比例由参数updateNeighborProbability控制。而将待更新节点经过一跳，二跳到达的节点存在sCand里面，供后面更新邻居的时候选择。

然后，对sNeigh中每一个选中的待更新的邻居n，利用启发式搜索(getNeighborsByHeuristic2)在sCand中选出最多M个点，将它们作为n的邻居存储在n的数据结构对应的位置。

第三步，更新待更新节点data_point的邻居。这个与添加节点类似：从当前图的从最高层逐层往下寻找直至节点的层数+1停止，寻找到离data_point最近的节点，作为下面一层寻找的起始点。2）从data_point的最高层依次开始往下，每一层寻找离data_point最接近的ef_construction_（构建HNSW是可指定）个节点构成候选集，再从候选集中利用启发式搜索选择M个节点与data_point相互连接.

4. 搜索节点

当我们构建好HNSW之后，就可以查询了，也就是给定一个向量(目标)，搜索最近的k个向量。也就是寻找图中，离目标点最近的k个点。HNSW利用分层的特性，先从最高层的入口点(enterpoint)开始，每一层寻找离目标点最近的点，作为下一层的入口，知道第0层。那么第0层的入口已经离目标向量很近了，所以后面的搜索就快多了。这里分两步来介绍：

1. 0层以上，从enterpoint开始，寻找离目标最近的点。
2. 0层，寻找最近的k个点。

4.1 第0层以上

0层以上比较简单，从enterpoint开始，遍历它的邻居，从邻居(包括自己)中找到离目标最近的点a。如果点a不是enterpoint，则下一次从点a开始以同样的模式搜索。如果点a和enterpoint是同一个点，也就是说，它的邻居包括自己所有点中，自己是离目标最近的点，则该层搜索结束。

以上图为例，假设c0为enterpoint，白色点e为目标。则先计算c0和c0的邻居(c1,c2)到e的距离，找到离e最近的点，是c2。因为c0和c2不是同一个点，那么现在以c2为当前点，计算它的邻居(含c2)中离目标最近的，是c3。现在，以c3为当前点，找寻它的邻居(含c3)中离目标最近的点，是自己。那么这一层搜索结束。c3作为下一层的enterpoint开始继续去下一层搜索。

0层以上的搜索代码如下：

 tableint currObj = enterpoint_node_; dist_t curdist = fstdistfunc_(query_data, getDataByInternalId(enterpoint_node_), dist_func_param_); for (int level = maxlevel_; level > 0; level--) { bool changed = true; while (changed) { changed = false; unsigned int *data; data = (unsigned int *) get_linklist(currObj, level); int size = getListCount(data); metric_hops++; metric_distance_computations+=size; tableint *datal = (tableint *) (data + 1); /* jeven: the for loop finds the nearest node in the current level, set the nearest obj into currObj, nearest dis to curdist */ for (int i = 0; i < size; i++) { tableint cand = datal[i]; if (cand < 0 || cand > max_elements_) throw std::runtime_error("cand error"); dist_t d = fstdistfunc_(query_data, getDataByInternalId(cand), dist_func_param_); if (d < curdist) { curdist = d; currObj = cand; changed = true; } } } } // jeven: until here, fins the nearest node, assign to currObj

4.2 第0层

经过第0层以上的搜索后，基本0层的入口点离目标比较接近了。那么在第0层，就要从入口点开始，找到离目标最近的不多于ef_construction个点，再从中选择最近的k个点返回。如何寻找最近的ef_construction个点，这个在前面几节多次提到。

简单的思想是：维护一个长度不大于ef_construction的动态list，记为W。每次从动态list中取最近的点，遍历它的邻居节点，如果它的邻居没有被遍历过，那么当结果集小于ef_construction，或者该节点比结果集中最远的点离目标近时，则把它添加到W中，如果该点没有被标记为删除，则添加到结果集。如果添加后结果集数量多于ef_construction，则把最远的pop出来。此种思想有点类似于BFS，只不过不同的是，这里的动态list是一个优先级队列，每次pop的是离目标最近的点。另外，结果集的数量有一个上限，需要不断的更新里面的点。

 // jeven: 记录遍历过的节点 visited_array[ep_id] = visited_array_tag; // jeven: 停止条件:动态list为空，前面把enterpoint已经添加进来了 while (!candidate_set.empty()) { // jeven:弹出当前最近的点 std::pair<dist_t, tableint> current_node_pair = candidate_set.top(); if ((-current_node_pair.first) > lowerBound) { break; } candidate_set.pop(); tableint current_node_id = current_node_pair.second; int *data = (int *) get_linklist0(current_node_id); size_t size = getListCount((linklistsizeint*)data); // jeven: 遍历当前点的邻居 for (size_t j = 1; j <= size; j++) { int candidate_id = *(data + j); // 如果当前点已经遍历过，则跳过 if (!(visited_array[candidate_id] == visited_array_tag)) { // jeven: 将该点标记为遍历过 visited_array[candidate_id] = visited_array_tag; char *currObj1 = (getDataByInternalId(candidate_id)); dist_t dist = fstdistfunc_(data_point, currObj1, dist_func_param_); // jeven: 如果结果集的size小于ef，或者该点距离小于结果集中的最大值 if (top_candidates.size() < ef || lowerBound > dist) { candidate_set.emplace(-dist, candidate_id); if (!has_deletions || !isMarkedDeleted(candidate_id)) top_candidates.emplace(dist, candidate_id); if (top_candidates.size() > ef) top_candidates.pop(); // jeven: 更新当前结果集中离目标最远的距离 if (!top_candidates.empty()) lowerBound = top_candidates.top().first; } } } } return top_candidates;

5. 总结

1.  HNSW采用类似跳表的思想，在高层跳过大量离目标点较远的点，从而快速定位到离目标较近的点，从而缩小搜索范围。
2.  HNSW在构图时采用启发式搜索选择连接邻居节点，从而防止出现不连通图的情况。
3. 搜索过程中维护动态list，从而减少遗漏的情况。

但是HNSW的缺点就是，除了保存数据之外，还需要一定的内存维护图的关系，而且每个节点分配固定的内存，其中有些没有使用而造成一定的浪费。