二维前缀和

大家好，欢迎来到IT知识分享网。

1、概念：

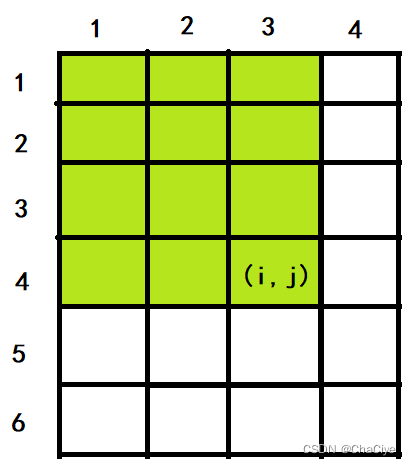
• 二维前缀和：S[i, j] = S[i – 1, j] + S[i, j – 1] – S[i – 1, j – 1] + a[i, j]（求的是坐标 (i, j) 左上部分所有元素的和。也就是绿色区域的所有元素的和）

2、二维前缀和S[i, j]如何计算：

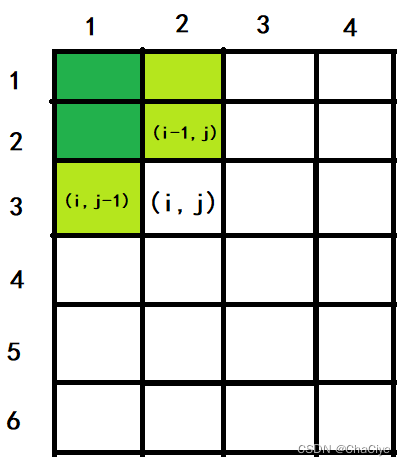
①、”S[i – 1, j]” 表示是坐标 (i – 1, j) 左上角所有元素和（绿色区域）。

②、”S[i, j – 1]” 表示是坐标 (i, j – 1) 左上角所有元素和。”S[i – 1, j] + S[i, j – 1]” 会导致深绿色区域重复多加1次。

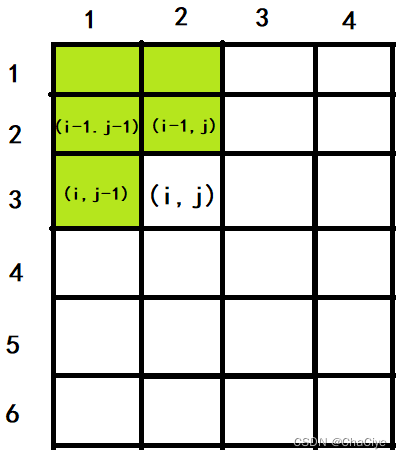
③、”S[i – 1, j] + S[i, j – 1] – S[i – 1, j – 1]” 就是为了除去深绿色区域重复多加的1次。

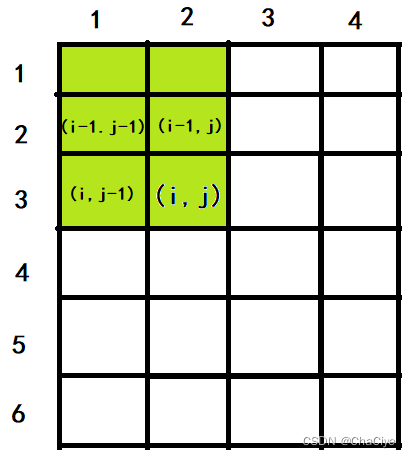
④、这时还差一个坐标点 (i, j) 没有加，所以最后是 “S[i – 1, j] + S[i, j – 1] – S[i – 1, j – 1] + a[i, j]”

3、子矩阵中所有数的和该如何计算：

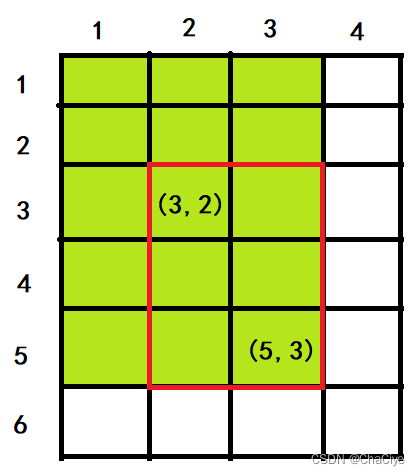
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中（红色方框区域）所有数的和该如何计算？

假设 “x1=3，y1=2″、”x2=5、y2=3”

①、”S[x2, y2]” 表示是坐标 (5, 3) 左上角部分所有元素和（绿色区域）。

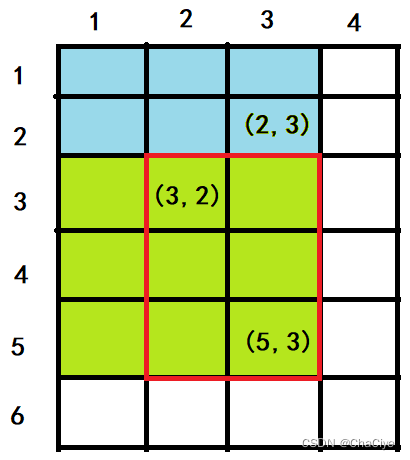
②、”S[x1 – 1, y2]” 表示是坐标 (2, 3) 左上角部分所有元素和（蓝色区域）。

③、”S[x2, y2] – S[x1 – 1, y2]” 就等于剩下的绿色区域。

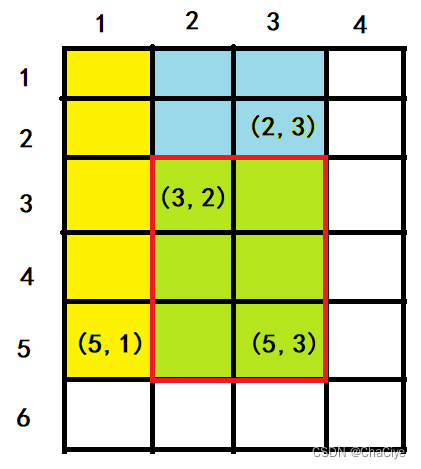
④、”S[x2, y1 – 1]” 表示是坐标 (5, 1) 左上角部分所有元素和（黄色区域）。

⑤、”S[x2, y2] – S[x1 – 1, y2] – S[x2, y1 – 1]” 就等于剩下的绿色区域。

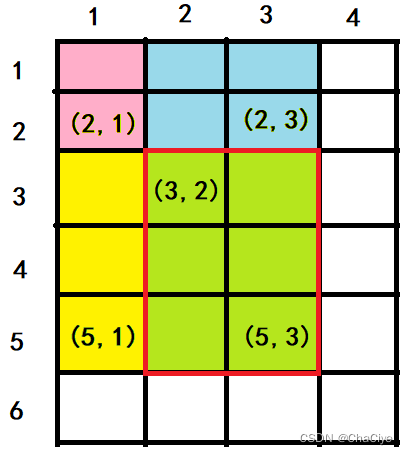
⑥、由于坐标 (2, 1) 的粉色区域多减了1次，所以要再加一次粉色区域，所以最后要加上 “S[x1 – 1, y1 – 1]”。

结论：

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和：

S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

4、代码实现——摘录AcWing：

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1, y1, x2, y2 表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

 输入格式：

第一行包含三个整数 n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数 x1, y1, x2, y2，表示一组询问。

 输出格式： 

共q行，每行输出一个询问的结果。

 数据范围：

#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m, q; int a[N][N], s[N][N]; int main() { scanf("%d%d%d", &n, &m, &q); for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { scanf("%d", &a[i][j]); } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; //求前缀和。 } } while (q--) { int x1, y1, x2, y2; scanf("%d%d%d%d", &x1, &y1, &x2, &y2); printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]); //算子矩阵的和。 } system("pause"); return 0; }