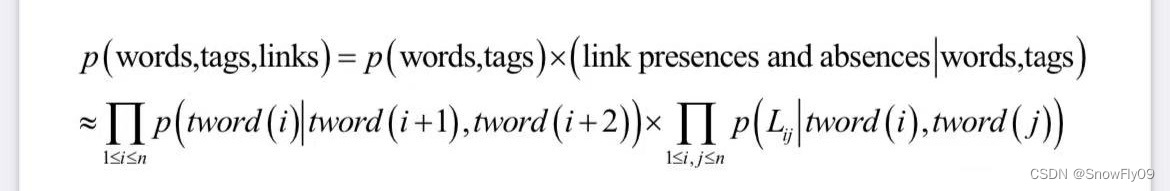【NLP】句法分析

大家好，欢迎来到IT知识分享网。

研究过程

句法规则涵盖的信息

两种不同的句法结构

依存结构

短语结构

将词组成对应的短语结构，然后将各种嵌套的短语结构混合在一起就变成了句子

句法分析

两个目的

1. 判断输入的句子是否符合语法
2. 识别句子各部分语法元素，同时生成句法树

两个准备

1. 语言的形式化描述
2. 句法分析技术

形式语言（详细内容在编译原理中）

形式语言的定义

$G=(N,\sum ,P,S)$，其中 N 是非终结符集合，sum 是终结符集合，P 是规则集合$P=(\alpha \to \beta )$，alpha 中至少包含一个非终结符，S 为起始符

推导的定义

如果$\alpha \beta \gamma$是总词汇表克林闭包中的符号串，且$(\beta \to ϵ)\in P$，故$\alpha \beta \gamma ={>}_G\alpha ϵ\gamma$
$=>^+ $表示传递闭包，也就是$X_n$到$X_{n+1}$经过 n（n>=1）步推导
$=>^* $表示自反和传递闭包，也就是$X_n$到$X_{n+1}$经过 n（n>=0）步推导

最左，最右和规范推导

没步推导只改写最左边的非终结符，称为最左推导，同理有最右推导，最右推导称为规范推导

句型与句子

$\alpha \beta \gamma$是一个句型，若该句型中不包含非终结符，则称为句子，所有句子构成的集合就被称为语言，记为 L（G），形式化描述为： L ( G ) = { x ∣ x ∈ ∑ , S = > G + x } L(G) = \{x|x \in \sum, S =>^+_Gx \} L(G)={
x∣x∈∑,S=>G+​x}

正则文法

$A\to Bx$左线性正则文法，A/B 为非终结符，x 为终结符
$A\to xB$右线性正则文法

上下文无关文法（2 型文法）

$A\to \alpha$，其中 A 为非终结符，alpha 为单词表的克林闭包

上下文有关文法（1 型）

$\alpha A\beta \to \alpha \gamma \beta$，其中 A 为非终结符，其他几项都属于单词表的克林闭包，gamma 至少包含了一个字符

无约束文法

最基础的$\alpha \to \beta$

上下文无关文法的二义性

形式语法

用来规定语言中允许出现的结构的形式化说明，这里我们重点介绍 CFG 上下文无关文法

上下文无关文法的语法 G

CFG 的特性

Chomsky 范式

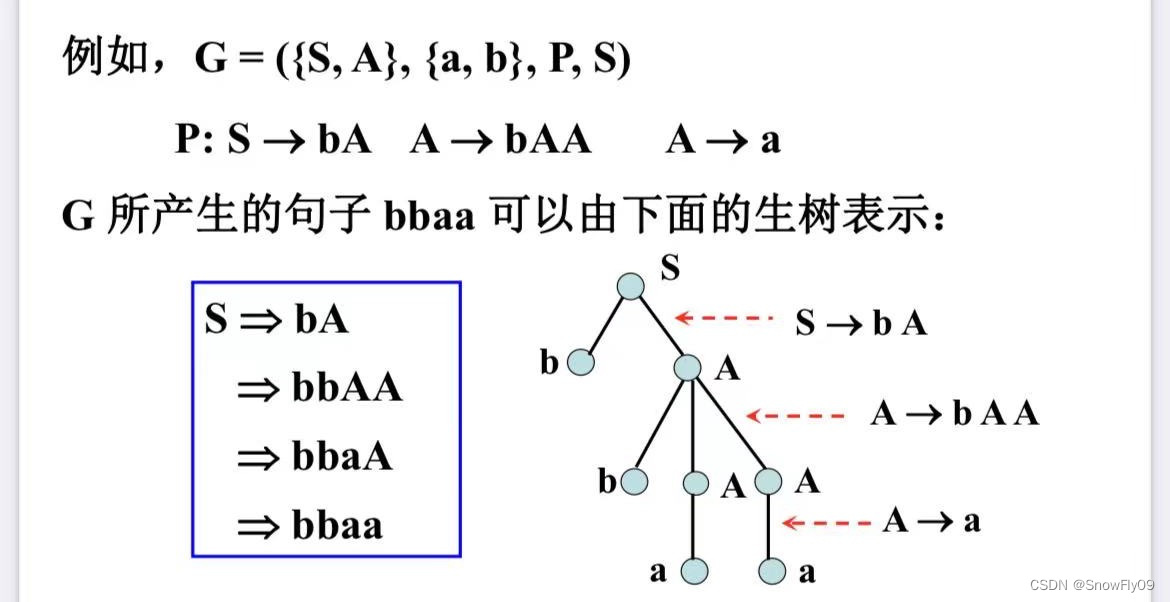
应用句法规则构建语法树

Cocke-Kasami-Younger Parsing

CYK 的识别矩阵

构造步骤

首先将$t_{0,0}=0$，然后往主对角线填上所有单词（非终结符）
然后考虑$t_{i,i+1},i=0,\dots ,n-1$这一对角线，对于输入句子$x=w_1{w}_2\dots w_n$开始分析
如果有 $A\to w_{i+1},则t_{i,i+1}=A$,即，对于主对角线上每一个终结符，所有可能推导出他的非终结符写在右边主对角线的上方
然后一层一层向上叠加，$A\to BC,B\in t_{i,k},C\in t_{k,j}=>A\in t_{i,j}$
判断句子 x 是由文法 G 产生的充要条件就是 t（0，n）=S

优缺点

几种常见的歧义

词性歧义/名词修饰歧义（形容词修饰的究竟是哪个名词）/介词短语修饰歧义（动作的状态修饰的对象不明）/边界歧义（Jim and Jane from LA）

PCFG 概率上下文无关文法

treebank

参数

假设

上下文无关：$P(N_{kl}^j\to \gamma |wordsoutside(w_k,w_i))=P(N_{kl}^j\to \gamma )$
祖先节点无关：$P(N_{kl}^j\to \gamma |ancestorNode)=P(N_{kl}^j\to \gamma )$

HMM 与 PCFG 的比较

定义动态规划表

$\pi (i,j.,X)$由非终结符 X 推导出子串的最大概率
目标是计算：$\underset{t\in \tau (s)}{\max }p(t)=\pi (1,n,S)$

取 max，可以得到是$VP\to VP,PP$

句法分析的程序化表达

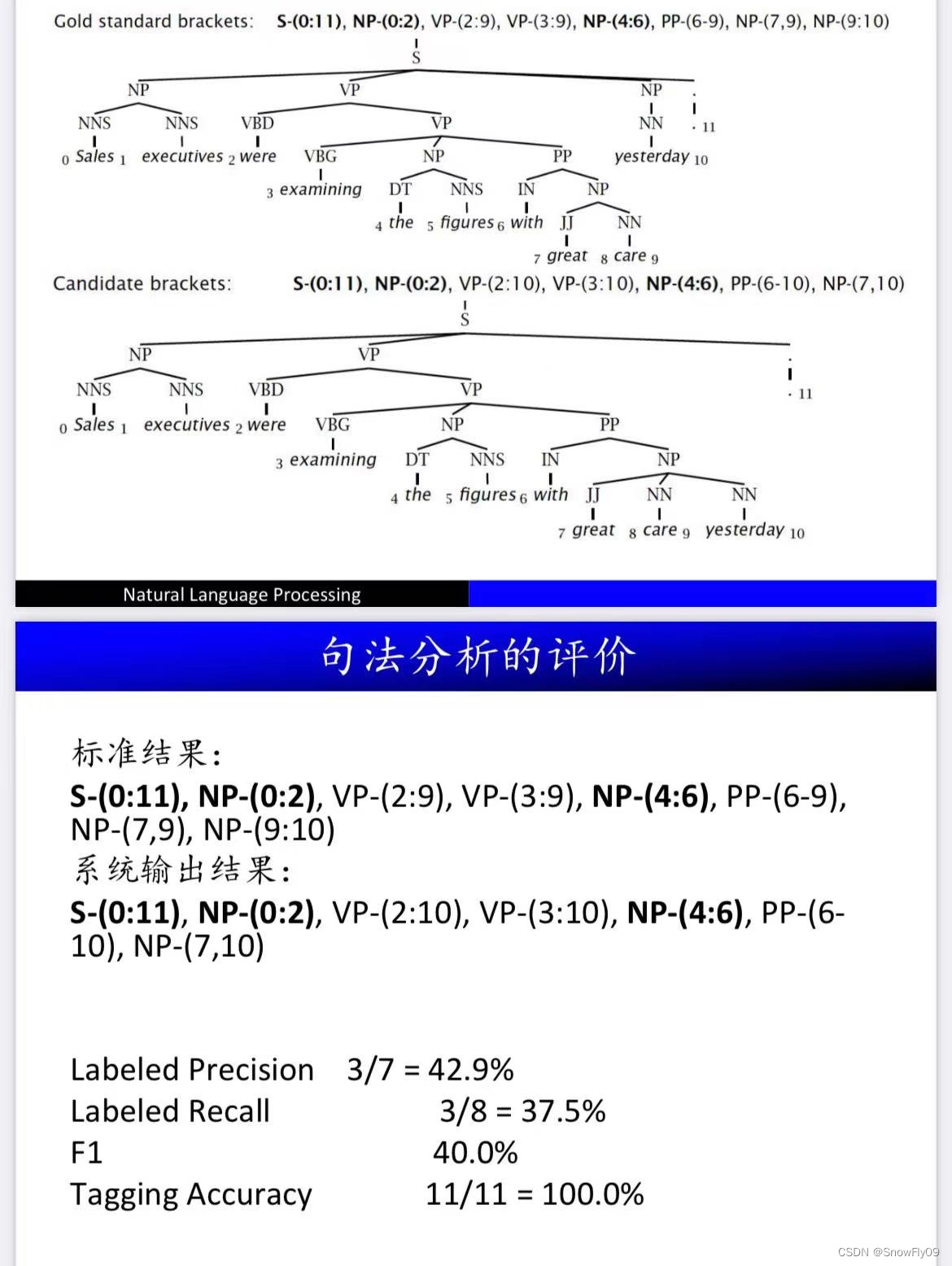
句法分析的评价

依存语法分析

在依存语法理论中，处于支配地位的成分称为支配者，而处于被支配地位的称为从属者；用有向边来表示依存关系，支配者处于发出端，从属者处于接收端

依存树

子节点依存于父节点

依存投射树

依存语法要求

依存句法分析器

分析算法

生成式的分析方法

采用联合概率模型$Score(x,y|\theta )$，生成一系列依存句法树，并且对每一个进行概率打分，最后选择分数最高的分析结果作为输出
e.g.二元词汇亲和模型&选择偏好模型

递归生成模型：每个词的左子节点和右子节点由各自的马尔可夫模型产生，左子节点从右向左产生，直到无法继续获得子节点；右子节点从左向右产生，直到无法获得子节点。这一方法是自顶向下的递归方法。

判别式的分析方法

采用条件概率模型$Score(x|y,\theta )$，使目标函数$\prod _{i=1}^{n}Score(x_i|y_i,\theta )$最大的 theta 作为模型的参数
e.g.最大生成树模型：整棵句法树的打分是树中各条边打分的加权和
$S(x,y)=\sum w\cdot f(i,j)$，f(i,j)表示 y 中的依存关系，如果树中 xi 与 xj 有依存关系则为 1，没有为 0. w 为使用样本训练出来的权值

决策式分析方法

基于约束满足的分析方法

依存句法分析器的评价指标

短语结构与依存结构的转换

汉英句法结构对比

语义分析

语义的分类

格语法

三条基本规则

$S\to Modality+Proposition$
$P\to V+C_1+\dots +C_n$
$C\to K+NP$

格表

施事格/工具格/承受格/使乘格/方位格/客体格…

分析步骤

语义网络

概念依存理论

词义消歧

有监督的词义消歧方法

无监督的词义消歧

在本处不做解释，例子有上下文分组辨识，可以寻找其他文章查看

基于词典信息的消歧

语义角色标注

句法分析器-候选论元剪除-论元识别-论元标注-后处理

候选论元剪除