fft/fftshift在通信系统中的作用（结合MATLAB说明）

大家好，欢迎来到IT知识分享网。

文章仅为个人理解，不足之处敬请指正

一、FFT物理意义

一个模拟信号，经ADC采样后就变成了数字信号，根据奈奎斯特采样定理可知，采样频率要大于被采信号最大频率的两倍，采样得到的数字信号就可以做FFT变换了。N个采样点，经过FFT之后，就可得到N个点的FFT结果，为了方便进行FFT运算，通常N取2的整数次方。

假设采样频率为Fs，信号频率为F，采样点数为N，那么FFT变换之后就是一个为N点的复数，每个点就对应有一个频率点，这个点的模值，就是该频率值下的幅度特性。假设原始信号的峰值为A，它跟FFT结果的幅度的关系为：FFT的结果的每个点(除第一个点直流分量之外)的模值就是A的N/2倍，而直流分量的模值是其实际模值的N倍，而每个点的相位就是该频率下的信号的相位。

FFT运算后第一个点(n=1)表示直流分量(即0Hz)，而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半,另一半移到最后)则表示采样频率Fs。这中间被N-1个点平均分成N等份，每个点的频率依次增加，例如某点n所表示的频率为：Fn=(n-1)*Fs/N。

由上述的公式可以看出，Fn所能分辨到的频率为Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分辨到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。总之，如果要提高频率分辨力，则必须增加采样点数，也即采样时间。

二、fftshift

为什么要在FFT之后用到fftshift呢?

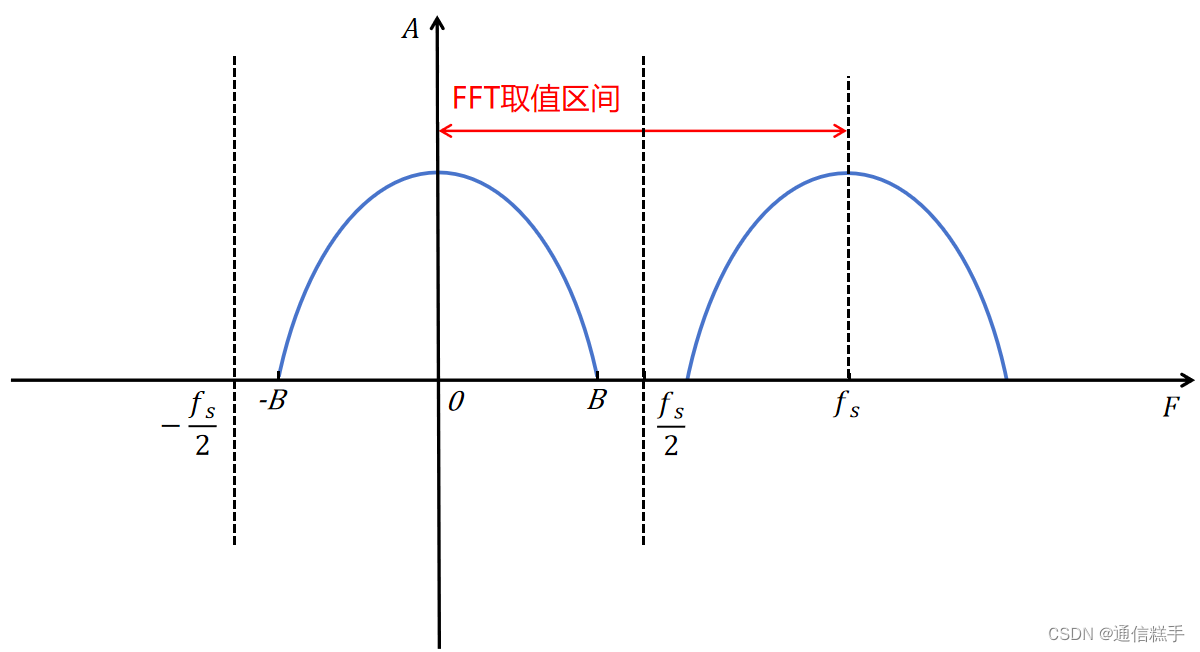
我觉得这个问题可以从采样定律的角度来说。以基带实信号为例，我们都知道时域以fs采样就是频域以fs平移延拓，因为采样之后的信号的频谱会在fs/2产生混叠，所以实信号采样率fs/2要大于等于带宽，即fs>2B，如下图1所示。

 图1 FFT取值窗口

MATLAB在对序列做FFT的时候，相当于是取了频谱上[0,fs]的部分，由于频谱是按Fs周期延拓，所以[fs/2,fs]部分的频谱与[-fs/2,0]部分的一样，如果你想看[-fs/2,fs/2]的部分(也即上图红线区间所示)那就需要做fftshitt，将零频分量移到序列中间。需要注意的是实信号和复信号经过FFT变换所得的结果是有所区别的，前者关于原点对称，是双边谱，后者只含有正频域部分，为单边谱，具体区别请看后续分析。

三、调用方法

X＝fft(Signal)；

X＝fft(Signal,N)；

Y = fftshift(X)；

Y= fftshift(X,dim)；

1.作用：交换行向量的左右两半部分。

2.在FFT里的作用：将零频分量移动到数组中心。

3.用MATLAB进行谱分析时注意：

（1）函数FFT返回值的数据结构具有对称性。

（2）做FFT分析时，幅值大小与FFT选择的点数有关，但不影响分析结果，要得到真实的振幅值的大小，只需要将得到的变换结果乘2/N(零频乘1/N)即可。

四、MATLAB仿真示例

1.实信号的频谱分析

示例：假设一个实信号：直流分量为3v，信号1幅值1.5、频率40Hz、相位45度，信号2幅值2.0、频率80Hz、相位90度。

数学表达式：Signal_12 = 3+1.5*cos(2*pi*40*t+45/180*pi)+2.0*cos(2*pi*80*t+90/180*pi)

采样频率512，采样点数512，故频率分辨率为1Hz。由上述分析，Fn=(n-1)*Fs/N，第n个点对应的频率就是(n-1)，所以实际频率 f=(0:N-1)*Fs/N，0Hz，40Hz，80Hz所对应的频点会出现相应的峰值，又因其为双边谱（由于周期延拓，-40和-80频点的峰值会以fs进行频谱搬移），故在频点（-40+512=472）和（-80+512=432）亦会出现峰值。实信号的频谱特点是关于原点对称，为双边谱。

% Nyquist频率为fs/2，整个频谱图是以Nyquist频率为对称轴 % 因此只需考察0~Nyquist频率范围内的幅频特性 clc; clear; close all; %% 初始参数 % 假设一个信号:直流分量为3v,信号1幅值1.5、频率40Hz、相位45度,信号2幅值2.0、频率80Hz、相位90度 DC = 3; % 直流分量 a1 = 1.5; % 信号1幅值 a2 = 2.0; % 信号2幅值 f1 = 40; % 信号1频率 f2 = 80; % 信号2频率 p1 = 45/180*pi; % 信号1相位(弧度) p2 = 90/180*pi; % 信号2相位(弧度) fs = 512; % 采样频率 Ts = 1/fs; % 采样周期 N = 512; % 采样点数(即fft变换点数) t = 0:Ts:Ts*(N-1); % 采样点 %% 数据处理 Singal_1 = a1*cos(2*pi*f1*t+p1); % 信号1 Singal_2 = a2*cos(2*pi*f2*t+p2); % 信号2 Signal_12 = DC + Singal_1 + Singal_2; % 叠加信号 y1 = fft(Singal_1,N); % 进行fft变换 y2 = fft(Singal_2,N); y12 = fft(Signal_12,N); y12_shift = fftshift(y12); % 将0频搬至于绘图中心 f = (0:N-1)*fs/N; % 频率序列,总长fs,fs/N为分辨率 f0 = f - fs/2; % 0频中心的频率序列 %% 频域实际幅值 % 为了与真实振幅对应，需要进行幅值变换 % 对于直流分量，实际幅度为fft后模值的1/N，其他的为2/N y1_abs = abs(y1)*2/N; y2_abs = abs(y2)*2/N; y12_abs = [abs(y12(1,1))*1/N,abs(y12(1,2:end))*2/N]; % n=1为直流分量(0Hz)，需单独转换 y12_shift_abs = [y12_abs(:,N/2+1:end),y12_abs(:,1:N/2)]; %% 绘图 % 信号1 figure(1); subplot(3,1,1) %信号1,时域 plot(t,Singal_1); title('Signal-40hz-时域'); xlabel('t/s'),ylabel('幅值'); grid on; subplot(3,1,2) %频域 plot(f,y1_abs); title('Signal-40hz-频域'); xlabel('f/Hz'),ylabel('幅值'); axis([0 fs 0 (max(y1_abs)+0.5)]); grid on; subplot(3,1,3) %频域(0~Nyquist) plot(f,y1_abs); title('Signal-40hz-频域(0~Nyquist)'); xlabel('f/Hz'),ylabel('幅值'); axis([0 fs/2 0 (max(y1_abs)+0.5)]); grid on; %信号2 figure(2); subplot(311) %信号2,时域 plot(t,Singal_2); title('Signal-80hz-时域'); xlabel('t/s'),ylabel('幅值'); grid on; subplot(312) %频域 plot(f,y2_abs); title('Signal-80hz-频域'); xlabel('f/Hz'),ylabel('幅值'); axis([0 fs 0 (max(y2_abs)+0.5)]); grid on; subplot(313) %频域(0~Nyquist) plot(f,y2_abs); title('Signal-80hz-频域(0~Nyquist)'); xlabel('f/Hz'),ylabel('幅值'); axis([0 fs/2 0 (max(y2_abs)+0.5)]); grid on; %信号12 figure(3); %叠加信号12,时域 subplot(211) plot(t,Signal_12); title('Signal-12-时域'); xlabel('t/s'),ylabel('幅值'); grid on; subplot(212) %频域 plot(f,y12_abs); title('Signal-12-频域'); xlabel('f/Hz'),ylabel('幅值'); axis([0 fs 0 (max(y12_abs)+0.5)]); grid on; figure(4); subplot(211) %0频搬移 plot(f0,y12_shift_abs); title('Signal-12-零频中心'); xlabel('f/Hz'),ylabel('幅值'); grid on; subplot(212) %频域(0~Nyquist) plot(f,y12_abs); title('Signal-12-频域(0~Nyquist)'); axis([0 fs/2 0 (max(y12_abs)+0.5)]); xlabel('f/Hz'),ylabel('幅值'); grid on;

2.实信号仿真结果

图2  信号1时频特性

图3  信号2时频特性

图4  实信号时频特性

图5  实信号频谱搬移

3.复信号的频谱分析

在数字通信系统中，所处理的数据形式一般是复信号(IQ信号)，其一般表达式为：  ，其中i为同向分量（实部），q为正交分量（虚部）。复信号的频谱特点是只存在正频域部分，为单边谱。

示例：假设一个单音复信号：实部与虚部幅值均为2，频率100Hz。

数学表达式：Signal_complex = 2*cos(2*pi*100*t) + 1i*2*sin(2*pi*100*t)

采样频率512，采样点数512，故频率分辨率为1Hz。由上述分析可得，实际频率 f=100Hz所对应的频点会出现相应的峰值，因其为复信号，故无镜像峰值，如下图6所示。

%% 复信号频谱分析 clc; clear; close all; %% 初始参数 % 假设一个单音复信号:实部与虚部幅值均为2，频率100Hz real = 2.0; % 实部幅值 imag = 2.0; % 虚部幅值 f = 100; % 单音频率 fs = 512; % 采样频率 Ts = 1/fs; % 采样周期 N = 512; % 采样点数(即fft变换点数) t = 0:Ts:Ts*(N-1); % 采样点 %% 数据处理 Singal_real = real*cos(2*pi*f*t); % 实部 Singal_imag = imag*sin(2*pi*f*t); % 虚部 Signal_complex = Singal_real + 1i*Singal_imag; % 复信号 y_complex = fft(Signal_complex,N); % 进行fft变换 y_complex_shift = fftshift(y_complex); % 将0频搬至于绘图中心 f = (0:N-1)*fs/N; % 频率序列,总长fs,fs/N为分辨率 f0 = f - fs/2; % 0频中心的频率序列 %% 频域实际幅值 % 为了与真实振幅对应，需要进行幅值变换 y_complex_abs = abs(y_complex)*2/N; y_complex_shift_abs = abs(y_complex_shift)*2/N; %% 绘图 figure(1); %复信号，频域 subplot(211) plot(f,y_complex_abs); title('Signal-complex-频域'); xlabel('f/Hz'),ylabel('幅值'); axis([0 fs 0 (max(y_complex_abs)+0.5)]); grid on; subplot(212) %0频搬移 plot(f0,y_complex_shift_abs); title('Signal-complex-零频中心'); xlabel('f/Hz'),ylabel('幅值'); grid on; 

 4.复信号仿真结果

图6 复信号零频搬移

总结：重点分析公式Fn=(n-1)*Fs/N即可，它是连接Matlab数据处理和实际数值的桥梁。