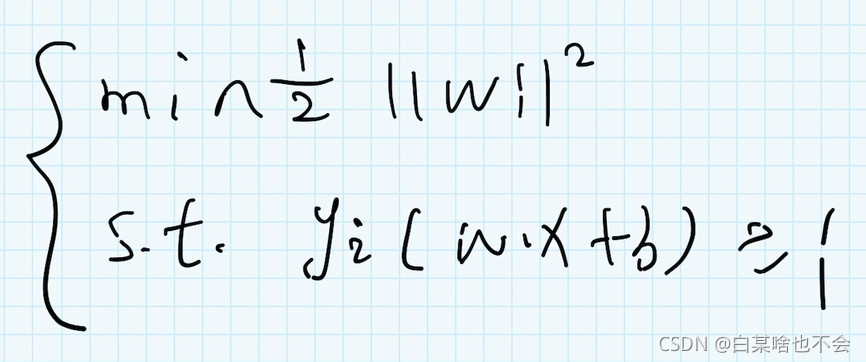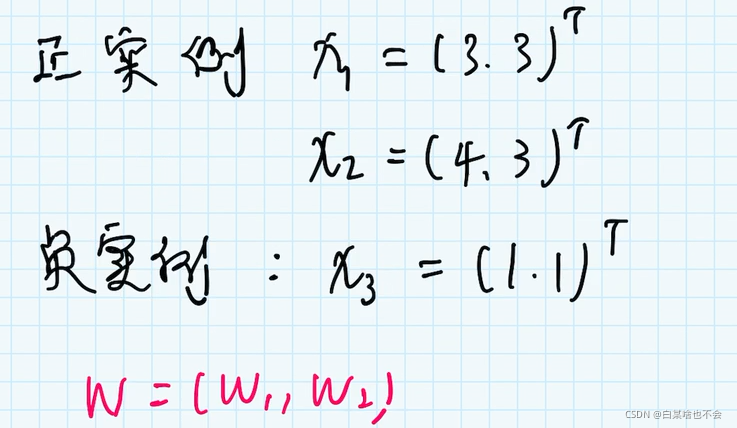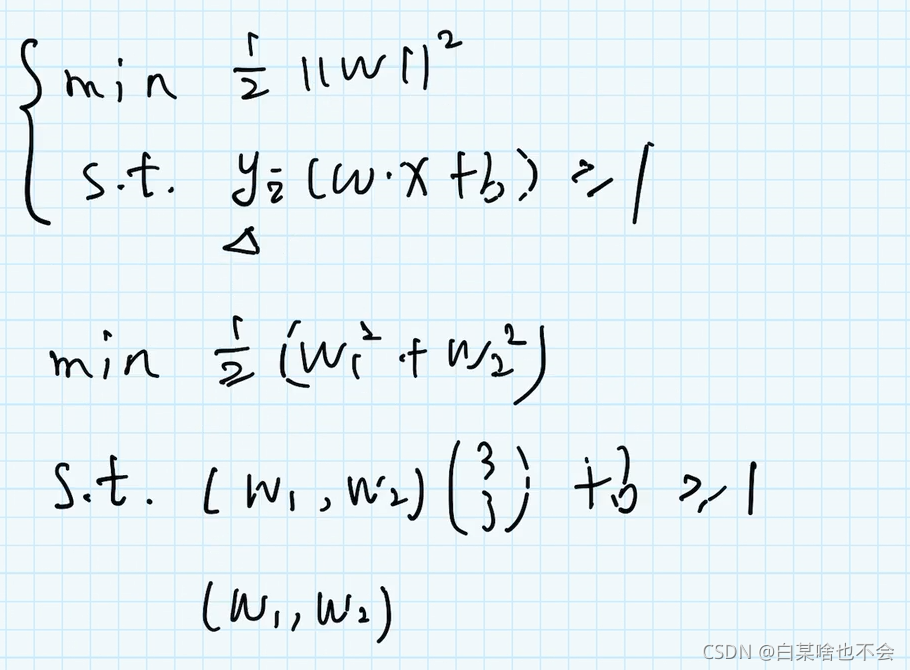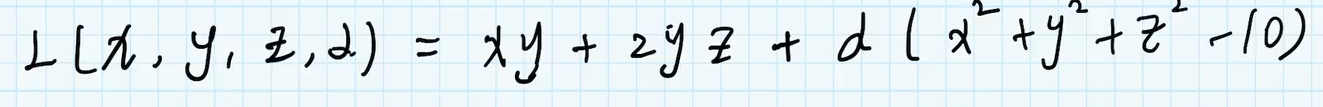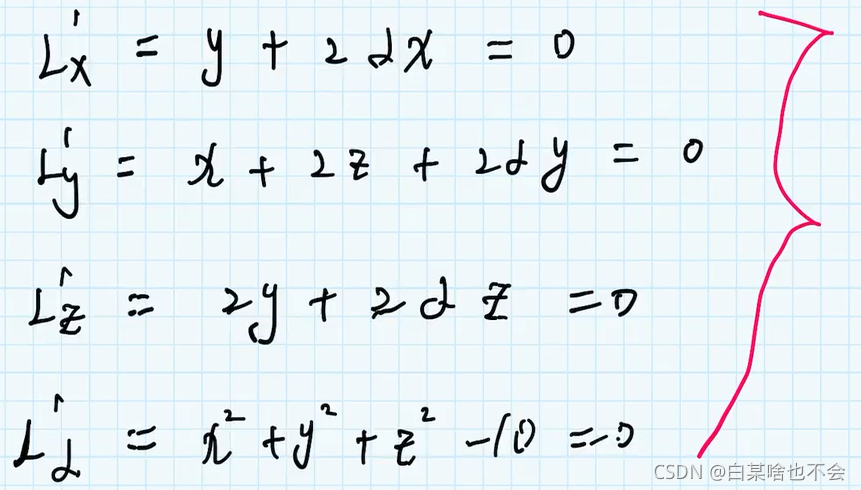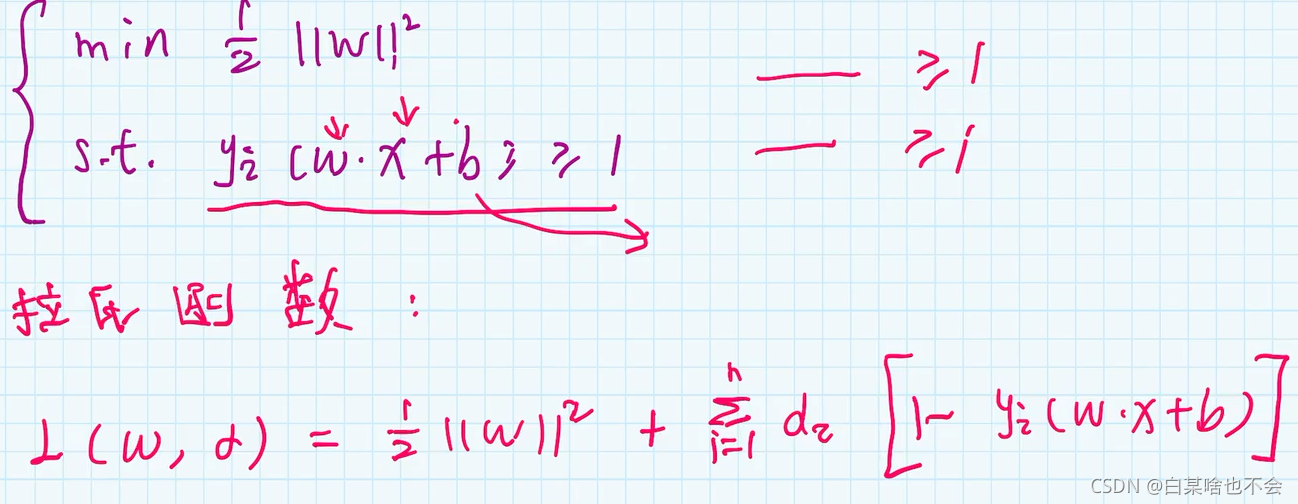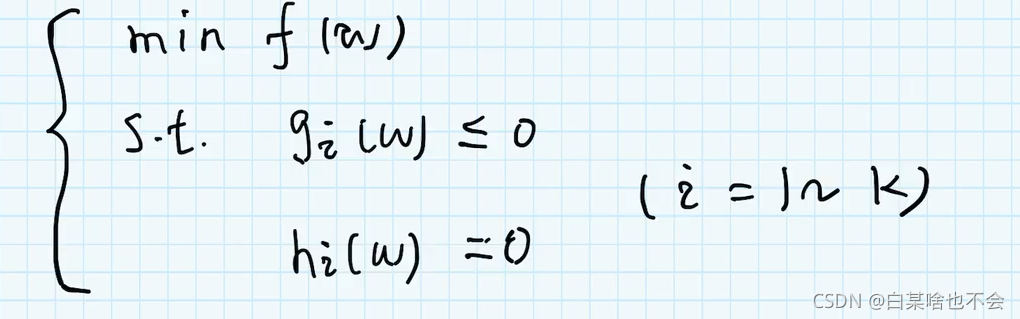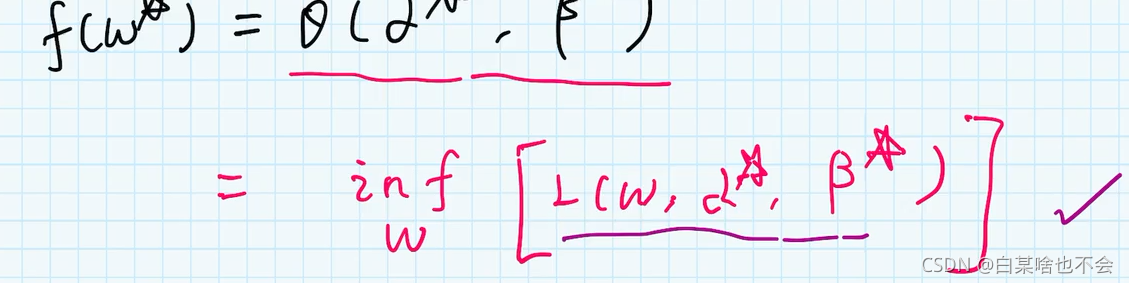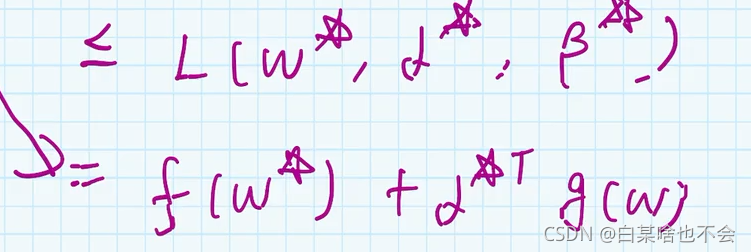大家好，欢迎来到IT知识分享网。
本文章是学习笔记，内容可能会有很多漏洞，如果有不正确的地方欢迎指正
一、SVM简述
1、概念
在机器学习领域，支持向量机SVM(Support Vector Machine)是一个有监督的学习模 型，通常用来进行模式识别、分类(异常值检测)以及回归分析。
二、硬间隔优化问题导出（Hard Margin）
1、线性模型
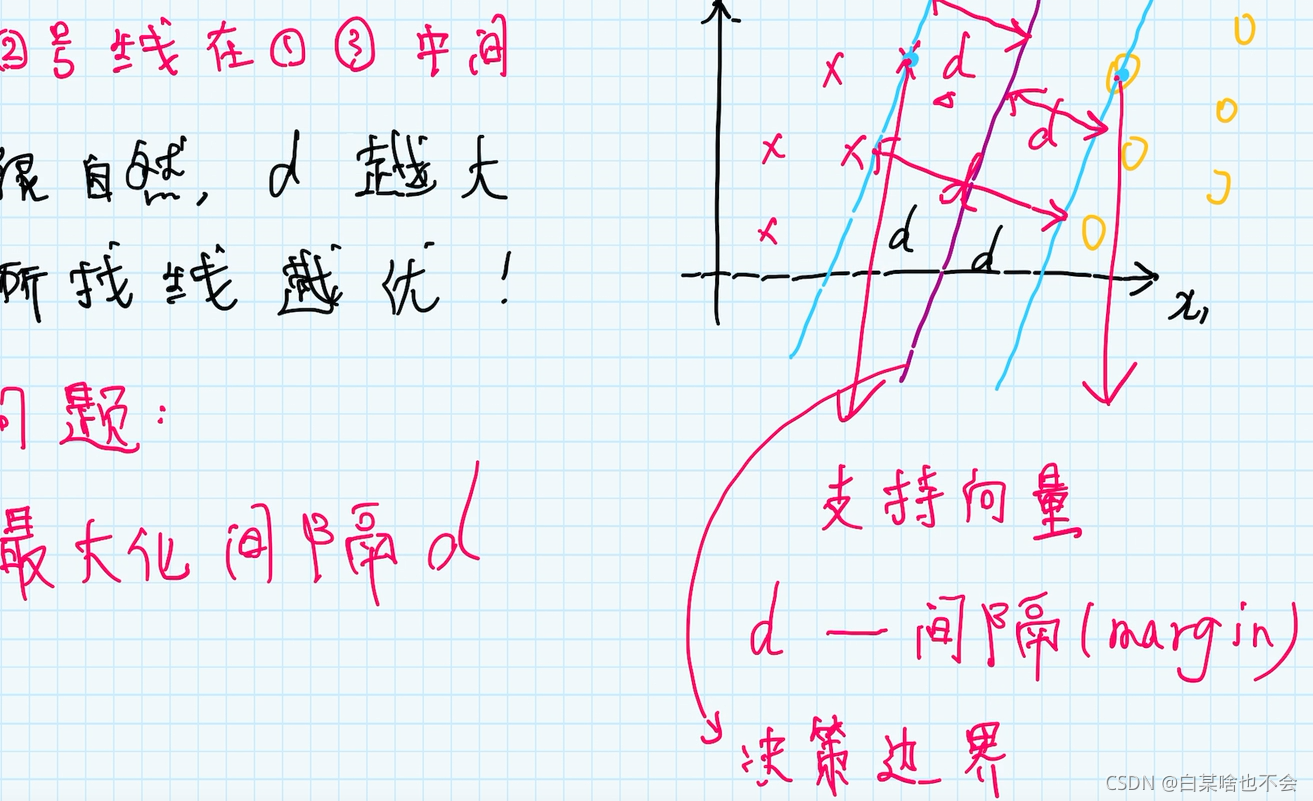
通过对决策边界的平移来决定，保证决策边界在两个刚刚碰到数据集的的中间位置
1.1、决策边界
数据集处于不同的位置，在决策边界的上方或者是下方，可分别归为+1类和-1类
2、线性可分SVM——硬件隔SVM
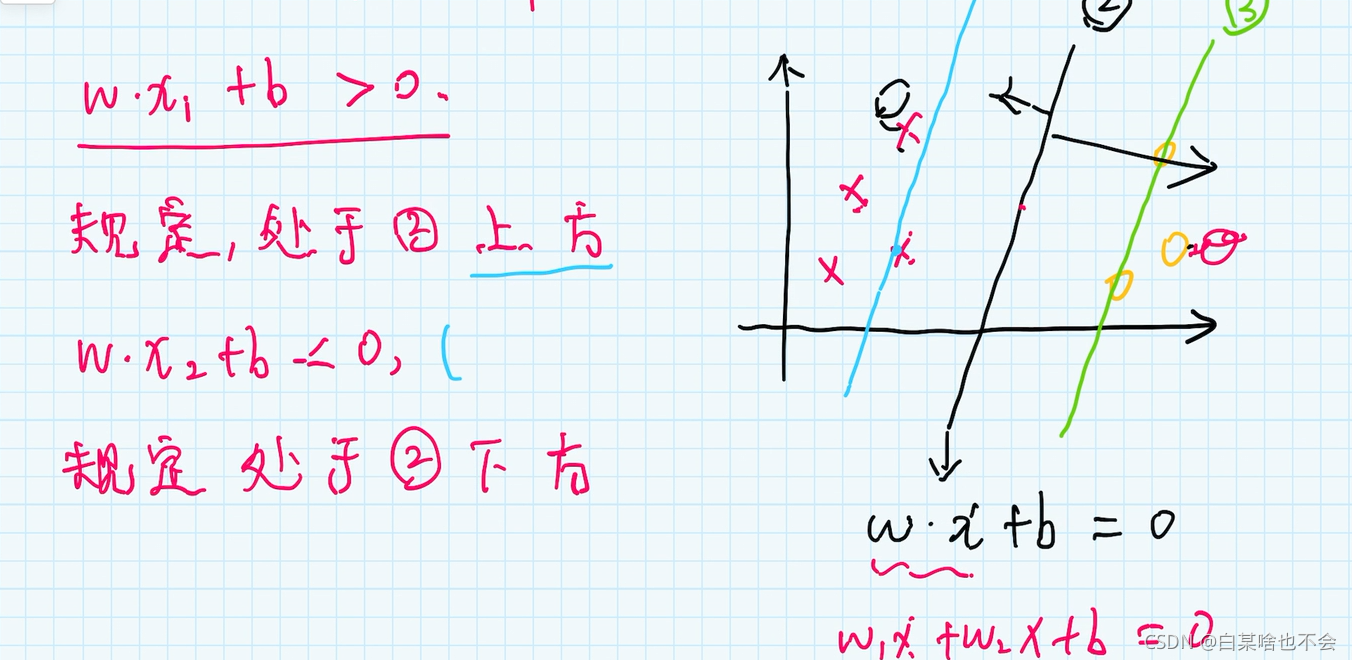
2.1、优化问题的导出
2.1.1、二维空间
2.1.2、三维空间
2.1.3、高维空间：超平面
2.1.4、最大化d（间隔）
直线2： ω x + b = 0 \omega x+b=0 ωx+b=0，而直线1、3都是由直线2平移过来的。
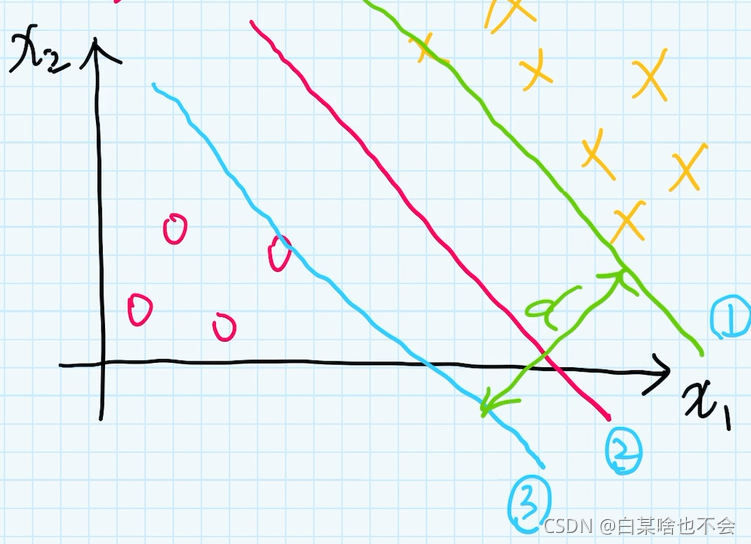
直线1： ω x + b = k \omega x+b=k ωx+b=k 直线3： ω x + b = − k \omega x+b=-k ωx+b=−k
对于两边都除以k，就得到 ω k x + b k = 1 \frac{\omega }{k}x+\frac{b}{k}=1 kωx+kb=1 和 ω k x + b k = − 1 \frac{\omega }{k}x+\frac{b}{k}=-1 kωx+kb=−1
对于直线2，两边都乘上 1 k \frac{1}{k} k1 得到 ω k x + b k = 0 \frac{\omega }{k}x+\frac{b}{k}=0 kωx+kb=0
这时我们可以得到三个全新的式子。
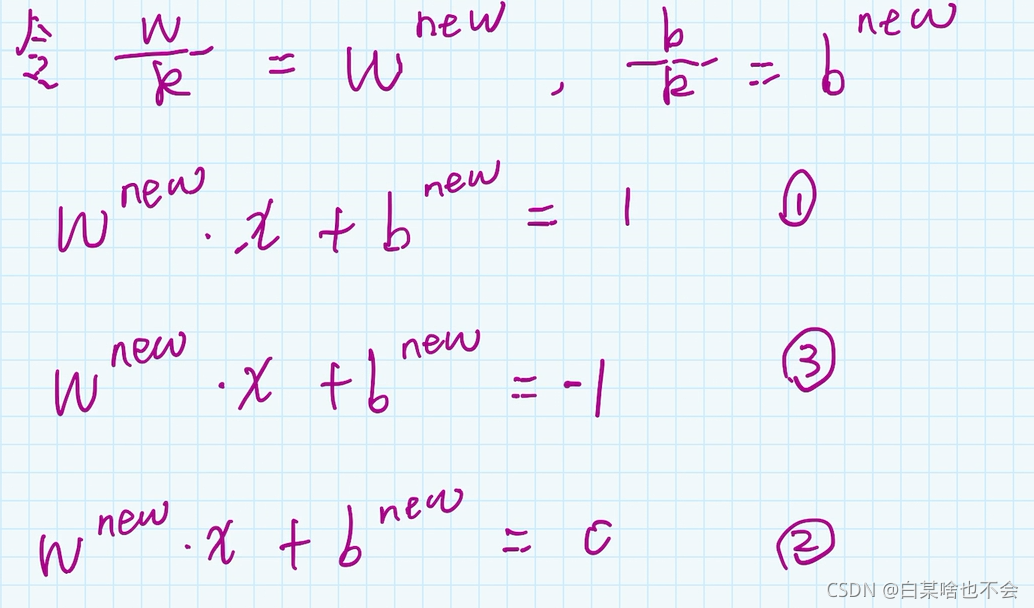
直线1： ω x + b = 1 \omega x+b=1 ωx+b=1
直线2： ω x + b = − 1 \omega x+b=-1 ωx+b=−1
直线3： ω x + b = 0 \omega x+b=0 ωx+b=0
注意：这里的 ω \omega ω 和 b b b 的与上文中的不相同，这里的是更新过后的 ω \omega ω 和 b b b
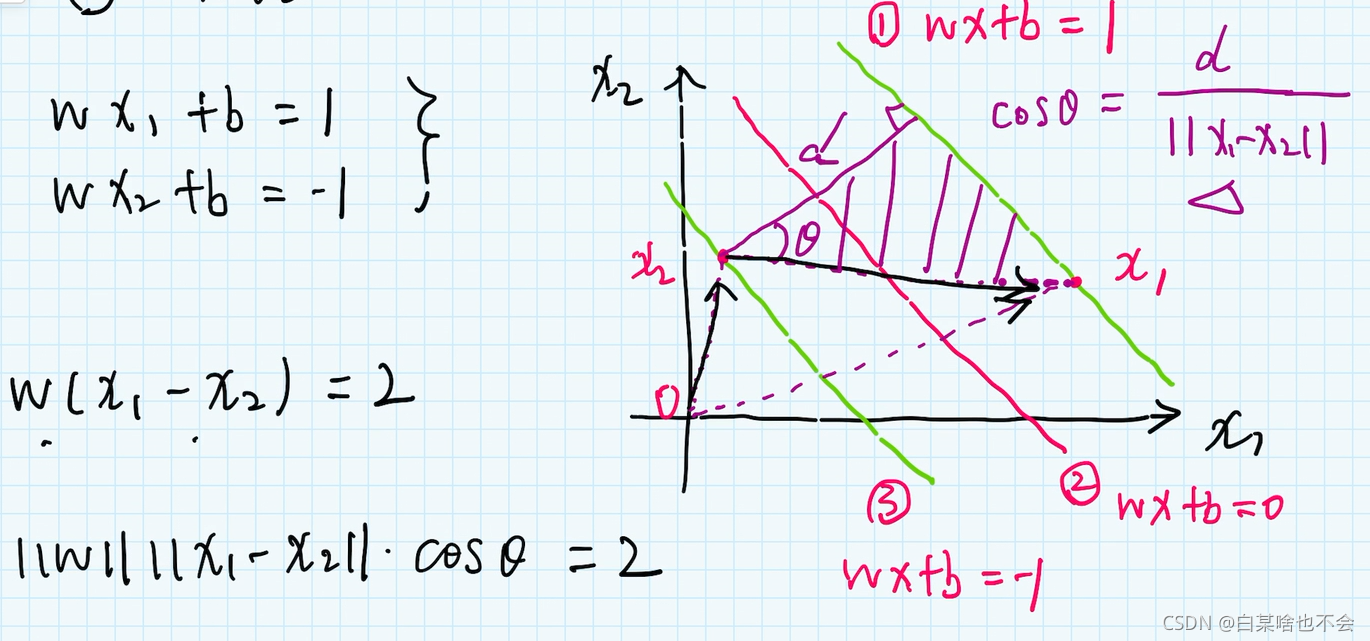
上文说过，这里的 x ， ω x，\omega x，ω是向量，所以 x 1 − x 2 x_1-x_2 x1−x2 得到的是 x 2 x 1 x_2x_1 x2x1 的那一段向量
之后是向量相乘，注意上面的 c o s θ cos\theta cosθ 可以由公式表示出d，与 ω \omega ω 建立关系 d = 2 ∣ ∣ ω ∣ ∣ d=\frac{2}{||\omega||} d=∣∣ω∣∣2。
m a x max max d 不就是 m i n min min 1 2 ∣ ∣ ω ∣ ∣ 2 \frac{1}{2}||\omega||^2 21∣∣ω∣∣2 （ ∣ ∣ ω ∣ ∣ ||\omega|| ∣∣ω∣∣表示为模长，在这个式子中是有根号的，所以这里需要平方一下，以便更好的计算）
问题的转化：最大化间隔 d ⇒ \Rightarrow ⇒ 最小化 1 2 ∣ ∣ ω ∣ ∣ 2 \frac{1}{2}||\omega||^2 21∣∣ω∣∣2
分析约束条件，发现不论数据集的分布在直线1上还是直线3下，都成立以下的式子
我们得到SVM优化问题：
3、例子
ω \omega ω 是法向量，这里设定的是二维平面，所以 ω \omega ω 有两个参数，就有了（ ω 1 \omega_1 ω1 和 ω 2 \omega_2 ω2）
接下来进行化简，改变了约束条件
最后解出 ω 1 \omega_1 ω1 和 ω 2 \omega_2 ω2 和 b
4、优化问题求解
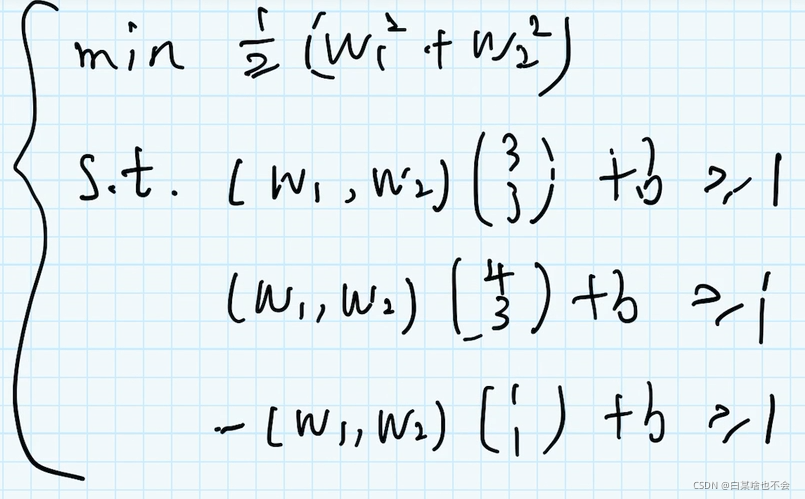
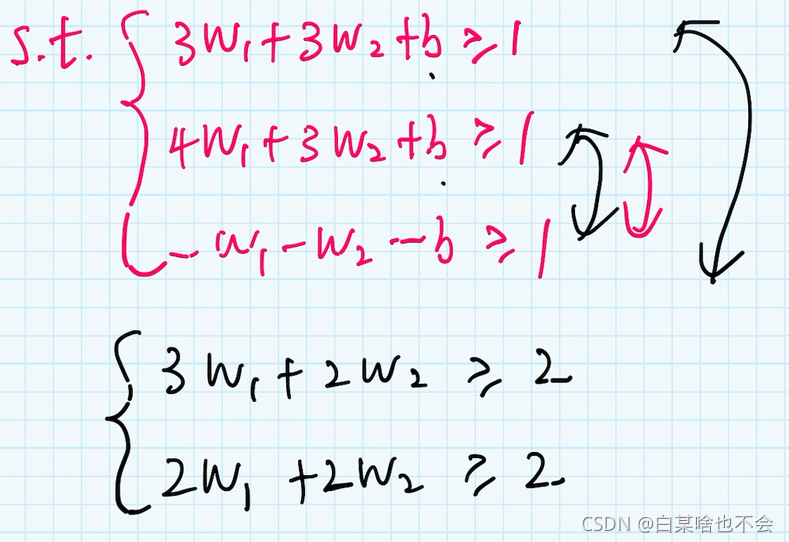
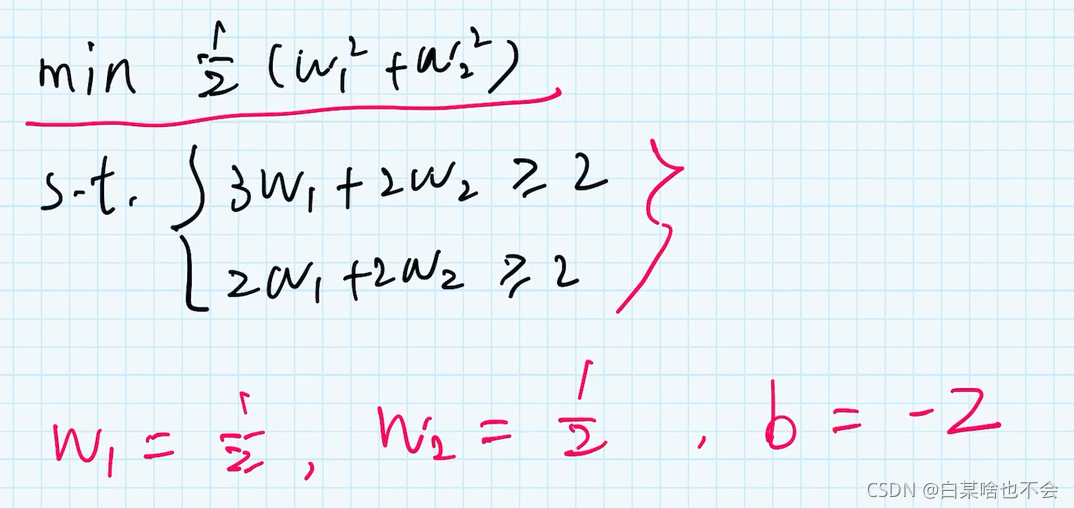
4.1、拉格朗日数乘法
拉氏乘数法主要用来求解带约束条件下的极值
例子
（1）构造拉氏函数
（2）分别求导数
（3）总结拉氏函数
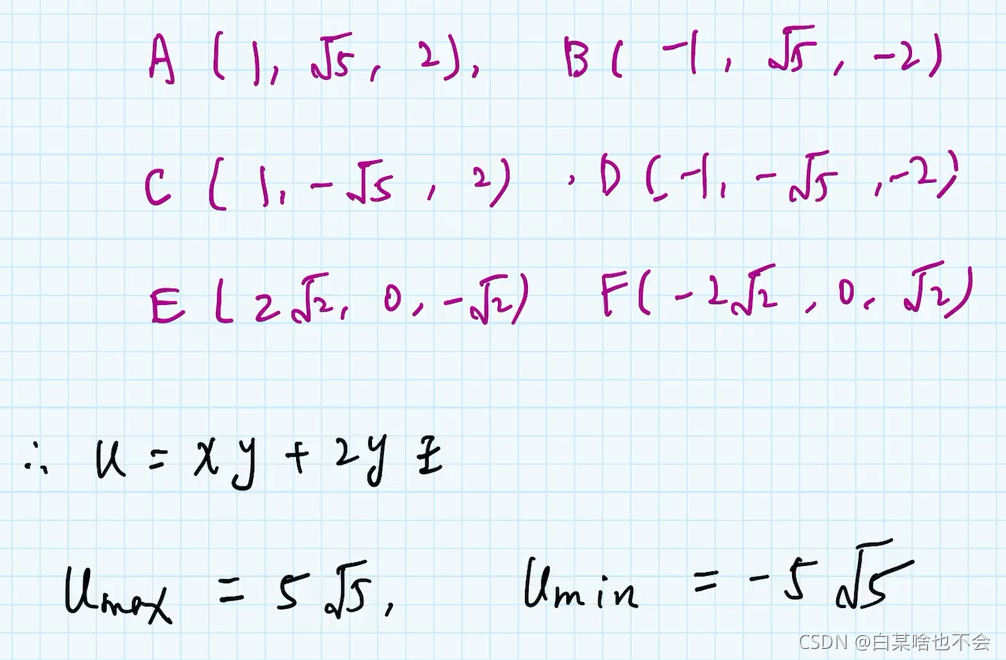
注意：在给出的约束条件中，s.t 有几个约束，就可以有几个参数（系数）
（4）SVM优化问题的拉氏函数
因为 x , ω x,\omega x,ω都是向量，所以有许多的约束条件，在这里我们将其写成连加的形式。
4.2、原问题与拉格朗对偶问题
4.2.1、原问题
4.2.2、对偶问题
先对拉氏函数求最小值，对参数 ω \omega ω求最小值（表示下确界的意思，就是无限的接近，有可能取的到，有可能取不到），在对拉氏函数求最大值（对 α , β \alpha,\beta α,β求最大值）
4.2.3、KKT条件
（1）定理1
如果 ω \omega ω 是原问题的最优解，而 α , β \alpha,\beta α,β 是对偶问题的最优解。 那么就有 f ( ω ) ≥ θ ( α , β ) f(\omega) \geq \theta(\alpha,\beta) f(ω)≥θ(α,β)
证明
先最小化原问题的最优解（意味着，随便带入一个 ω \omega ω 都比他大）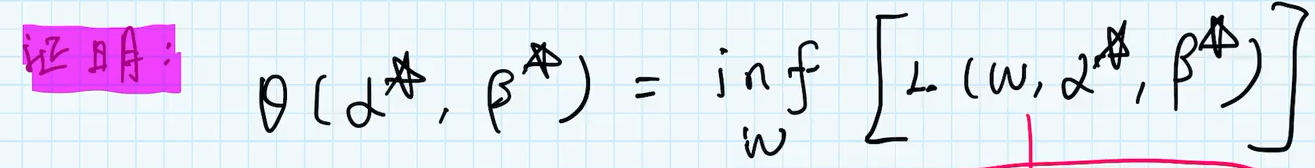
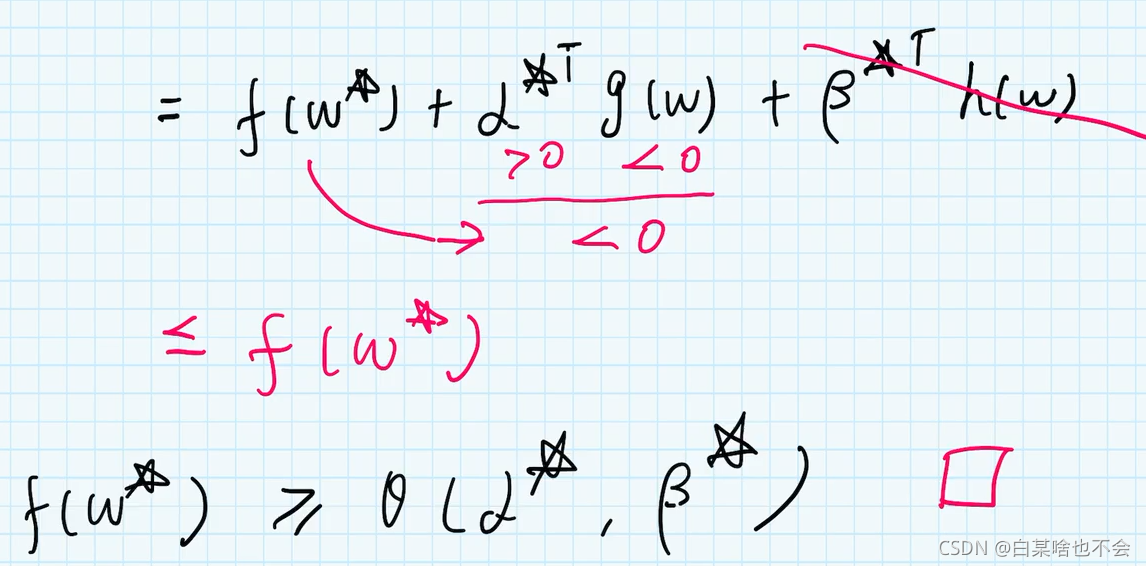
根据上文提到 h ( ω ) = 0 h(\omega)=0 h(ω)=0 和 g ( ω ) ⩽ 0 g(\omega)\leqslant0 g(ω)⩽0的条件，得到
（2）定理2：原问题与对偶问题之间的间距
（3）强对偶定理
拉氏函数的最小值，随便带入一个值都比它大
三、参考
https://www.bilibili.com/video/BV1A4411y7qK?from=search&seid=
本文章还未更新完毕未来会继续更新
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/116006.html
