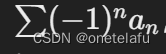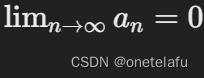大家好,欢迎来到IT知识分享网。
1. 比较法(Comparison Test)
使用条件:一个已知的收敛或发散的级数。
- 直接比较法(Direct Comparison Test):两个正项级数 ∑an , ∑bn 。
- 如果 an ≤ bn 且 ∑bn 收敛,则 ∑an 收敛。
- 如果 an ≥ bn 且 ∑bn 发散,则 ∑an 发散。
- 极限比较法(Limit Comparison Test):两个正项级数 ∑an 和 ∑bn,且
C是正的有限常数。
- 如果∑bn 收敛,则 ∑an 收敛。
- 如果∑bn 发散,则 ∑an 发散。
2. 比例法(Ratio Test)
通常适用于 n!的级数判断。
正项级数 ∑an,定义:
- 如果 L < 1,那么级数 ∑an 收敛。
- 如果 L > 1,那么级数 ∑an 发散。
- 如果 L = 1,需要使用其他方法判断。
- 注意的是,在an无法判断是否为正项级数时,使用如下判断:
- 此时如果 L < 1,那么级数 ∑an 绝对收敛,其余不变。
3. 根值法(Root Test)
通常适用于 含n次方 的级数判断。
一个级数 ∑an,定义:
- 如果 L < 1,那么级数 ∑an 绝对收敛。
- 如果 L > 1 或者 L=∞,那么级数 ∑an 发散。
- 如果 L = 1,需要使用其他方法判断。
4. 积分法(Integral Test)
假设 f(x) 是一个正的、连续的、单调递减的函数,并且 an=f(n)。
那么级数 ∑an 与 积分
收敛性相同。
- 如果 积分 收敛,那么级数 ∑an 也收敛。
- 如果 积分 发散,那么级数 ∑an 也发散。
5. 交错级数(Alternating Series Test)
一个交错级数
其中 an 为正且单调递减,
并且
那么级数收敛。
提一嘴:
- 级数 ∑an 收敛,指 部分和数列的极限 存在, lim (n→∞) Sn = s 存在 。 此时,一定有 lim (n→∞) an =0(级数收敛的必要条件)。
6. p-级数法(p-Series Test)
p-级数测试适用于形如:
的级数。
- 如果 p > 1,那么 级数 收敛。
- 如果 p ≤ 1,那么 级数 发散。
- (我喜欢把n分之一成为“临界点”。)
7.莱布尼茨判断 (Leibniz’s Test)
适用条件:交错级数。
对于一个交错级数,如果满足以下两个条件,则级数收敛:
1.单调递减:
an 是单调递减的,即对于所有的 n,有
2.趋于零:
an 的极限是零,即
PS:奇级数收敛,偶级数收敛,则级数收敛。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/116683.html

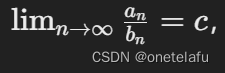 C是正的有限常数。
C是正的有限常数。