大家好,欢迎来到IT知识分享网。
目录
一、SVM介绍
1.1SVM基本概念
1.2线性可分支持向量
D0 和 D1 是 n 维欧氏空间中的两个点集。如果存在 n 维向量 w 和实数 b,使得所有属于 D0 的点Xi都有 wXi+b>0 ,而对于所有属于 D1 的点 则有 wXi+b<0 ,则称 D0 和 D1 线性可分。
如图:两类点被一条直线完全分开叫做线性可分。
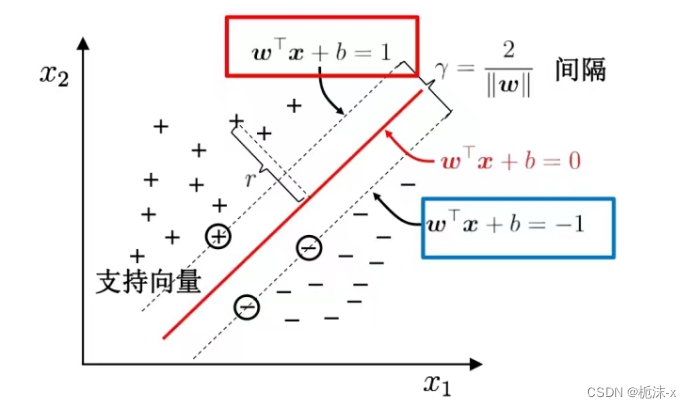
1.3最大间隔超平面
分割直线可能不止一条,为了保证鲁棒性,将会选择中间的一条直线。
鲁棒性是指系统或算法对于输入数据发生变化或异常情况时的稳定性和可靠性。一个鲁棒性强的系统能够在面对不同类型的输入数据时仍能保持良好的表现,并且能够有效地处理异常情况,而不会产生严重的错误或崩溃。
从二维扩展到多维空间中时,将 D0 和 D1 完全正确地划分开的 wx+b=0 就成了一个超平面。(w是权重,b是截距,训练数据就是训练得到权重和截距。)
为了使这个超平面更具鲁棒性,我们会去找最佳超平面,以最大间隔把两类样本分开的超平面,也称之为最大间隔超平面。
两类样本分别分割在该超平面的两侧;
两侧距离超平面最近的样本点到超平面的距离被最大化了。
支持向量:样本中距离超平面最近的一些点,这些点叫做支持向量。
1.4软间隔和硬间隔
软间隔和硬间隔用于描述分类器对数据的容忍程度和灵活性。
硬间隔:在一个线性可分的情况下,硬间隔SVM试图找到一个能够完全将不同类别的数据分开的超平面。这意味着不允许任何数据点出现在间隔边界之间。硬间隔SVM对异常值非常敏感,因为即使一个异常值的存在都可能导致无法找到一个完全将数据分开的超平面。
软间隔:在实际应用中,数据往往不是完全线性可分的,可能会存在一些噪声或异常点。软间隔SVM允许一些数据点出现在间隔边界之间,并引入了超参数 C(惩罚系数),控制了模型的复杂度和容错能力。较小的C值会导致容错能力较高(即更宽的缓冲区),可能会产生更多的错误分类(即间隔违规);较大的C值会导致容错能力较低,可能会产生更少的错误分类。
这样一来,软间隔SVM相对于硬间隔SVM具有更强的鲁棒性,能够更好地处理现实世界中的数据集。在实际应用中,软间隔SVM通常比硬间隔SVM更加常见,因为它能够更好地适应真实世界中的数据,对噪声和异常点有更好的容忍度。
1.5惩罚参数C
在支持向量机(SVM)中,惩罚参数 C 控制着分类器的复杂度和错误的容忍程度。
1. C太小:
当 C 很小时,模型会更加倾向于选择简单的决策边界,这可能导致模型对训练数据欠拟合。
意味着分类器对错误的容忍度较高,可能会允许一些训练样本被错误分类。
如果 C 过小,可能会导致高偏差(bias)和低方差(variance),这意味着模型对训练集和测试集中的数据都表现不佳。
2. C太大:
当 C 很大时,模型更倾向于选择复杂的决策边界,以准确地分类所有训练样本。
意味着分类器对错误的容忍度较低,可能会导致模型对训练数据过拟合。
过大的 C 可能会导致高方差和低偏差,这意味着模型在训练集上表现良好,但在未见过的数据上表现不佳。
为了找到最佳的 C 值,可以使用交叉验证来评估不同 C 值下模型的性能,通常采用网格搜索(Grid Search)或者随机搜索(Random Search)来搜索最佳的超参数组合。选择合适的惩罚参数 C 对于 SVM 模型的性能和泛化能力至关重要,需要在训练过程中进行调优和验证。
二、核函数
2.1核函数介绍
引入核函数的主要原因是为在SVM中,有时候很难找出一条线或一个超平面来分割数据集,这时候我们就需要升维(把无法线性分割的样本映射到高纬度空间,在高维空间实现分割)
核函数是特征转换函数,它可以将数据映射到高维特征空间中,从而更好地处理非线性关系。核函数的作用是通过计算两个样本之间的相似度(内积)来替代显式地进行特征映射,从而避免了高维空间的计算开销。
常用的核函数包括线性核函数、多项式核函数、高斯核函数、sigmoid核函数等。
线性核函数(Linear Kernel):线性核函数是最简单的核函数之一,它在特征空间中对应于输入空间的线性关系。线性核函数的定义如下:K(X, y) =( X^T )*y,其中,(x) 和 (y) 是输入空间中的两个向量。
多项式核函数(Polynomial Kernel):引入了一个多项式的非线性映射,将输入空间映射到更高维的特征空间。多项式核函数的定义如下:K(x, y) = ((x^T)* y + c)^d其中,(c) 是一个常数,(d) 是多项式的次数。
高斯核函数(Gaussian Kernel):也称为径向基核函数(Radial Basis Function, RBF),是一种常用的非线性核函数。它通过将输入空间映射到无穷维的特征空间来实现非线性变换。定义如下:
其中,σ 是高斯核的带宽参数,控制了样本之间相似度的衰减速度。σ 越小,样本之间的相似度下降得越快;σ 越大,样本之间的相似度下降得越慢
Sigmoid核函数(Sigmoid Kernel):是一种常用的非线性核函数,它模拟了神经网络中的激活函数。定义如下:
2.2核函数选择
假设特征数为N,训练数据集的样本个数为W,可按如下规则选择算法:
若N相对W较大,使用逻辑回归或线性核函数的SVM算法
若N较小,W中等大小(W为N的十倍左右),可使用高斯核函数的SVM算法
若N较小,W较大(W为N的五十倍以上),可以使用多项式核函数、高斯核函数的SVM算法
总之 ,数据大的问题,选择复杂一些的模型,反之,选择简单模型。
这些不同类型的核函数可以根据数据和问题的特点选择。线性核函数适用于线性可分或近似线性可分的数据,而多项式核函数、高斯核函数和Sigmoid核函数则适用于非线性可分的数据。在实际应用中,选择合适的核函数对于支持向量机的性能和准确性至关重要。
三、SVM优缺点及应用场景
3.1 SVM的优点
高效的处理高维特征空间:SVM通过将数据映射到高维空间中,可以处理高维特征,并在低维空间中进行计算,从而有效地处理高维数据。
处理线性和非线性问题:SVM在处理线性可分和线性不可分的数据时都能够取得良好的效果。通过使用核函数,SVM可以将数据映射到高维特征空间,从而处理非线性问题。
泛化能力强:SVM通过最大化分类间隔来构建最优的决策边界,从而在训练数据之外的新数据上表现出很好的泛化能力。这意味着SVM对未见过的数据也能进行准确的分类预测。
鲁棒性强:SVM在构建模型时只关注支持向量,即位于决策边界附近的样本点。这使得SVM对于噪声和异常值具有较好的鲁棒性,能够减少模型的过拟合风险。
3.2 SVM的缺点
对大规模数据集的计算开销较大:SVM的计算复杂度随着样本数量的增加而增加,特别是在大规模数据集上的训练时间较长。
对于非线性问题选择合适的核函数和参数较为困难:在处理非线性问题时,选择适当的核函数和相应的参数需要一定的经验和领域知识。
对缺失数据敏感:SVM在处理含有缺失数据的情况下表现不佳,因为它依赖于支持向量的定义。
SVM在处理小样本数据、高维特征空间和非线性问题时表现出色,但对于大规模数据集和缺失数据的处理相对困难。同时,在模型的解释性方面也存在一定的挑战。
3.3 SVM的应用场景
二分类问题:SVM最初被设计用于解决二分类问题,特别是在数据线性可分的情况下,SVM能够找到最优的超平面来准确地将两个类别分开。
多分类问题:虽然SVM最初是为二分类问题设计的,但也可以通过一对多或一对一策略扩展到多类别分类问题。一对多策略将每个类别与其他所有类别进行区分,而一对一策略则构建一组分类器来处理每对类别。
文本分类与情感分析:SVM在文本分类任务中表现出色,可以用于将文本分为不同的类别,如垃圾邮件识别、情感分析等。通过将文本表示为特征向量,SVM可以学习一个决策边界来准确地分类新的文本样本。
四、基于SVM实现鸢尾花分类预测
4.1 算法步骤
SVM算法可以分为以下几个步骤:
数据预处理:将数据集划分为训练集和测试集,并进行特征缩放(对数据进行标准化)。
构建模型:选择合适的核函数和惩罚系数,构建SVM模型。
训练模型:使用训练集对模型进行训练,通过最大化间隔来找到最优的超平面。
预测:使用训练好的模型对测试集进行预测。
4.2python实现
1. 数据预处理
from sklearn import datasets # 加载鸢尾花数据集 iris = datasets.load_iris() X = iris.data y = iris.target from sklearn.preprocessing import StandardScaler # 对特征进行标准化 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) from sklearn.model_selection import train_test_split # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42) 使用 datasets 模块加载了著名的鸢尾花数据集。特征缩放可以使不同特征具有相同的尺度,从而加速收敛并减小某些算法对特征尺度的不敏感性,使用 StandardScaler 将特征标准化,使得每个特征具有零均值和单位方差。random_state=42 保证了结果的可重复性。
2. 构建模型
# 定义参数网格 param_grid = { 'C': [0.1, 1, 10, 100], 'gamma': ['scale', 'auto'], 'kernel': ['rbf', 'linear'] } from sklearn.model_selection import GridSearchCV from sklearn.svm import SVC # 使用网格搜索找到最佳参数 grid_search = GridSearchCV(SVC(), param_grid, cv=5) grid_search.fit(X_train, y_train) print("Best parameters found: ", grid_search.best_params_) print("Best cross-validation score: ", grid_search.best_score_) 定义了用于网格搜索的参数网格。选择了 C (惩罚参数)、gamma (核系数) 和 kernel (核函数类型)作为要调优的参数。使用 GridSearchCV,在参数网格上进行了交叉验证,以找到最佳的SVM模型参数。cv=5 表示使用5折交叉验证。
3. 训练模型
# 使用最佳参数进行预测 best_svc = grid_search.best_estimator_ from sklearn.decomposition import PCA # 使用PCA将数据降维到2个主成分 pca = PCA(n_components=2) X_pca = pca.fit_transform(X_scaled) # 在降维后的数据上重新训练最佳SVC模型 X_train_pca, X_test_pca, y_train_pca, y_test_pca = train_test_split(X_pca, y, test_size=0.3, random_state=42) best_svc.fit(X_train_pca, y_train_pca) 网格搜索结果中提取出最佳的 SVM 模型。为了便于可视化,使用主成分分析(PCA)将数据降维到二维。降维后的数据再次被分割成训练集和测试集,然后用最佳的 SVM 模型进行训练。
4. 预测和决策边界绘制
import numpy as np # 创建一个网格以绘制决策边界 h = 0.02 # 网格步长 x_min, x_max = X_pca[:, 0].min() - 1, X_pca[:, 0].max() + 1 y_min, y_max = X_pca[:, 1].min() - 1, X_pca[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # 预测整个网格点的分类 Z = best_svc.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) 为了绘制决策边界,创建了一个网格。在网格上进行预测,以获得每个点的分类结果。
5. 输出与可视化
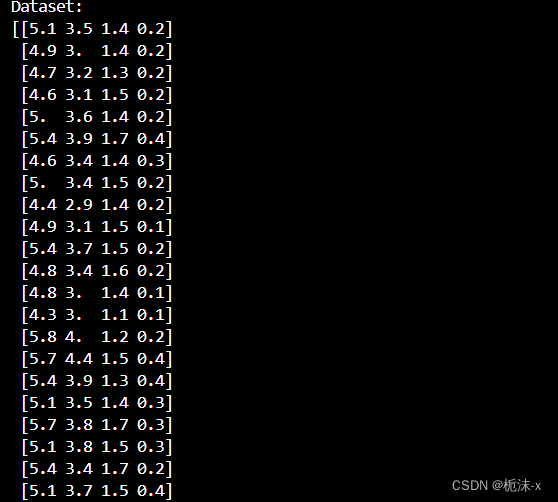
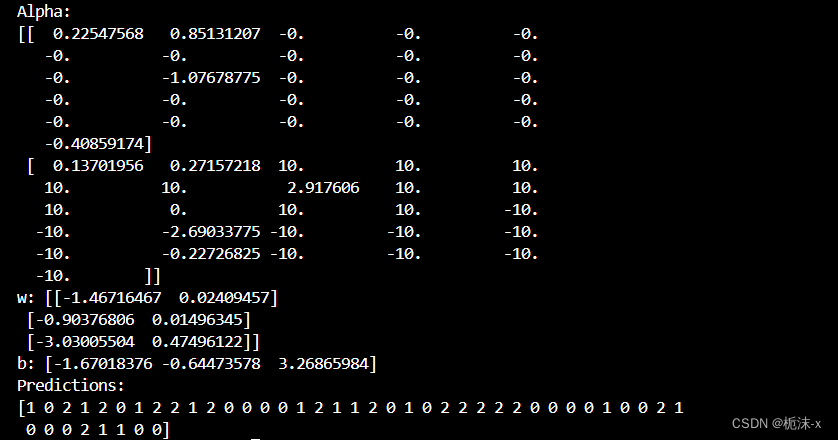
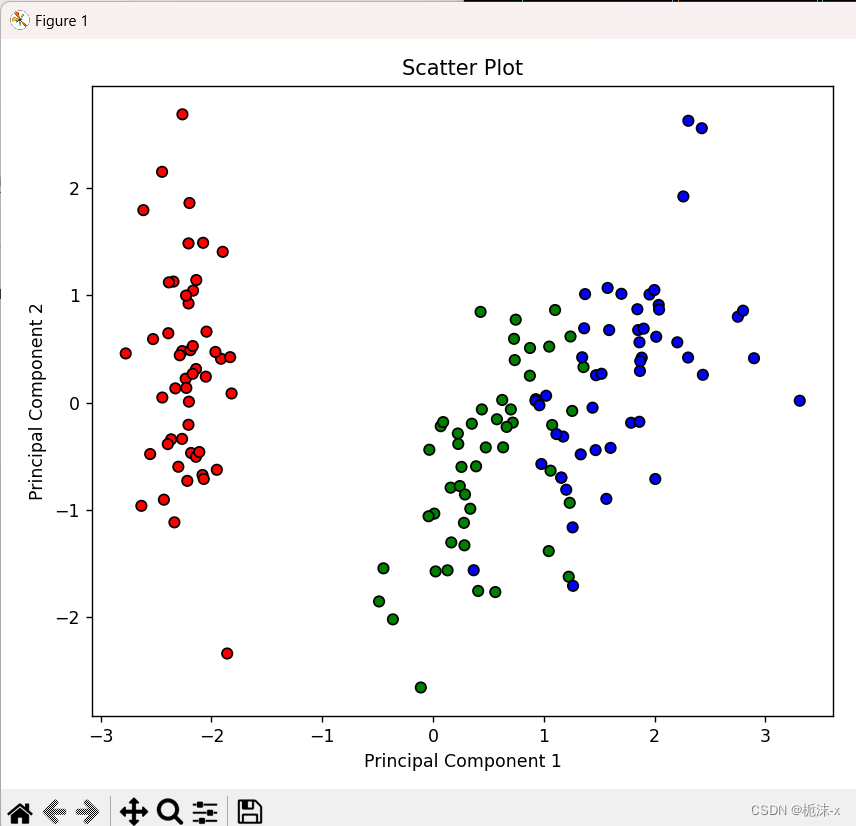
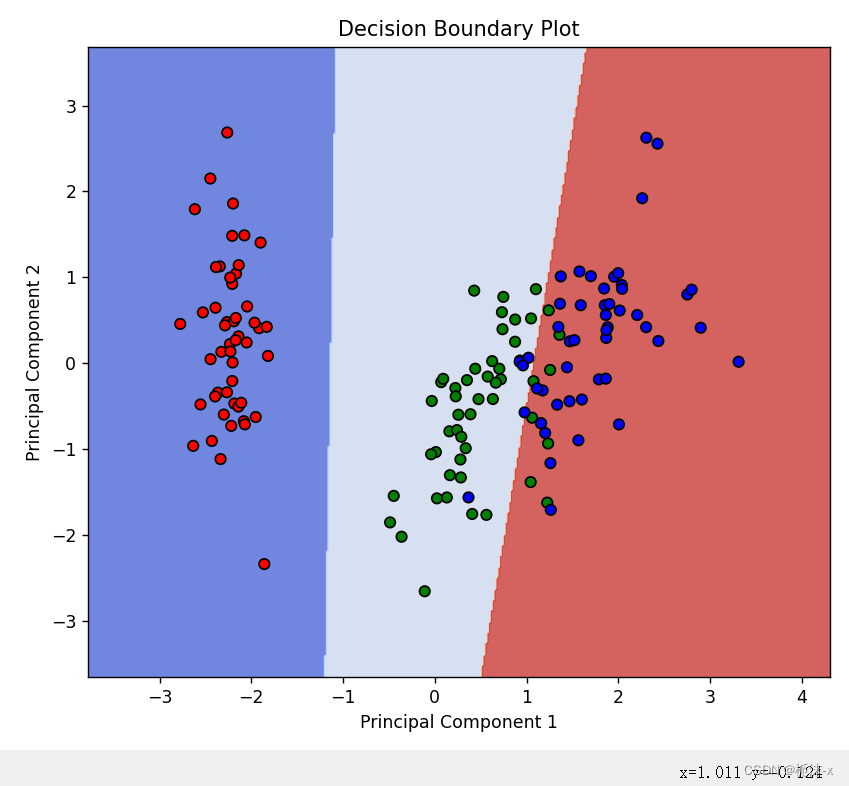
# 输出数据集 print("Dataset:") print(iris.data) # 输出α(拉格朗日乘子) print("Alpha:") print(best_svc.dual_coef_) # 输出w和b if best_svc.kernel == "linear": w = best_svc.coef_ b = best_svc.intercept_ print("w:", w) print("b:", b) # 输出预测结果 y_pred = best_svc.predict(X_test_pca) print("Predictions:") print(y_pred) import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap # 绘制散点图 plt.figure(figsize=(12, 6)) plt.subplot(121) plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, edgecolors='k', cmap=ListedColormap(['red', 'green', 'blue'])) plt.title('Scatter Plot') plt.xlabel('Principal Component 1') plt.ylabel('Principal Component 2') # 绘制决策边界图 plt.subplot(122) plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.coolwarm) plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, edgecolors='k', cmap=ListedColormap(['red', 'green', 'blue'])) plt.title('Decision Boundary Plot') plt.xlabel('Principal Component 1') plt.ylabel('Principal Component 2') plt.tight_layout() plt.show() 输出原始的鸢尾花数据集和支持向量的拉格朗日乘子。如果核函数是线性的,输出权重向量 w 和偏置 b。对测试集进行预测,并输出预测结果。最后,绘制了两个图:一个是降维后数据的散点图,另一个是加入决策边界的图,这样可以可视化分类效果。
这段代码进行了数据预处理,构建并训练了一个支持向量机(SVM)模型,通过主成分分析(PCA)降维并可视化了决策边界
4.3运行结果说明
散点图
决策边界图
五、总结
分类和回归的选择
通常情况下,当标签值是离散型变量时,我们将问题视为分类问题,而当标签值是连续性变量时,我们将问题视为回归问题。
在支持向量机(SVM)算法中,SVC用于分类,SVR用来做回归。
在分类问题中,我们的目标是将输入数据分为不同的离散类别。常见的分类算法包括逻辑回归、决策树、随机森林和支持向量机等。
在回归问题中,我们的目标是预测连续性变量的值。回归问题涉及到对输入数据进行建模,以预测一个或多个连续的输出变量。常见的回归算法包括线性回归、决策树回归、支持向量回归和神经网络等。
SVM的训练过程是一个凸优化问题,目标是最小化模型的结构风险。在求解过程中,SVM只关注那些位于决策边界附近的样本,它们被称为支持向量。这种特性使得SVM具有较好的鲁棒性和泛化能力。总体而言,SVM是一种强大的机器学习算法,能够处理高维空间的数据,并通过寻找最优超平面实现分类和回归分析。它在许多领域如图像识别、文本分类和生物信息学中都取得了广泛的应用。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/117226.html