【线性代数】矩阵变换

大家好，欢迎来到IT知识分享网。

一些特殊的矩阵

一，对角矩阵

1，什么是对角矩阵

表示将矩阵进行伸缩（反射）变换，仅沿坐标轴方向伸缩（反射）变换。

2，对角矩阵可分解为多个F1矩阵，如下：

二，剪切矩阵

1，什么是剪切矩阵

2，剪切矩阵的几何意义

3，剪切矩阵的特点

变换前后面积不变

三，正交矩阵

1，什么是正交矩阵？

2，正交矩阵的特点

（1）是方阵

（2）每个列向量都是单位矩阵

（3）每对列向量都正交

（4）正交矩阵的转置等于它的逆

3，正交矩阵的几何意义

只有旋转，无剪切，无伸缩，无反射

如下图所示，矩阵A表示绕X轴旋转60°，矩阵B表示绕Z轴旋转45°，C表示先按X轴旋转60°再按Z轴旋转45°，顺序不能颠倒。

若颠倒顺序，先绕Z轴旋转，再按X轴旋转，则：

四，投影矩阵

1，什么是投影矩阵？

将高维的变换到低维

谱分解

作用对象是对称矩阵，对称矩阵的特征向量正交。

本质：将一个复杂的变换分解为：旋转-伸缩-逆旋转

Q为单位特征向量组成的矩阵，即e1，e2，e3都是单位特征向量， $\Lambda$ 为特征值组成的对角矩阵。

过程解释（以2维为例）：原对称矩阵S具有2个特征向量，且特征向量都正交， $Q^{T}$ 矩阵实现了将特征基 e1，e2旋转到原来的基（1，0）（0，1）的过程，然后进行 $\Lambda$ 伸缩变换，即沿特征基的方向进行伸缩变换，最后再乘Q将特征基旋转回原来的位置。

谱分解的特殊点：

（1）对称矩阵的特征向量都正交，原来的基也是正交的，则仅进行正交变换（旋转）即可实现将特征基旋转为原来的基。

奇异值分解

奇异值分解与谱分解的区别只有，谱分解是旋转—伸缩—逆旋转，而奇异值分解是旋转—伸缩（可能有维度消除或维度扩充）—再旋转。奇异值分解的第二次旋转不是第一次旋转的逆旋转。

1，图+公式推导

待分解矩阵的变换如图，改变换将相互正交的向量 $v_{1}$ ， $v_{2}$ 变换到仍然相互正交的向量 $u_{1}$ ， $u_{2}$ ，伸缩量为 $\sigma _{1}$ ， $\sigma _{2}$ 。设 $V=[v_{1},v_{2}]$ ， $U=[u_{1},u_{2}]$ ， $\Sigma =\begin{bmatrix} \sigma _{1} &0 \\ 0 &\sigma _{2} \end{bmatrix}$

则 $MV=U\Sigma$ ，即 $M=U\Sigma V^{T}$

即 $M^{T}M=V\Sigma U^{T}U\Sigma V^{T}=V\Sigma ^{2}V^{T}$

即 $M^{T}MV=V\Sigma ^{2}$

所以 $M^{T}M$ 的特征向量为，特征值为 $\Sigma ^{2}=\begin{bmatrix} \sigma _{1}^{2} &0 \\ 0 & \sigma _{2}^{2} \end{bmatrix}$

同理 $MM^{T}$ 的特征向量为，特征值为 $\Sigma ^{2}=\begin{bmatrix} \sigma _{1}^{2} &0 \\ 0 & \sigma _{2}^{2} \end{bmatrix}$

综上，奇异值分解中 $M=U\Sigma V^{T}$ ，为 $MM^{T}$ 的特征向量，为 $M^{T}M$ 的特征向量。 $\Sigma$ 为 $MM^{T}$ 或 $M^{T}M$ 特征值的平方根。

为右奇异向量，为左奇异向量。

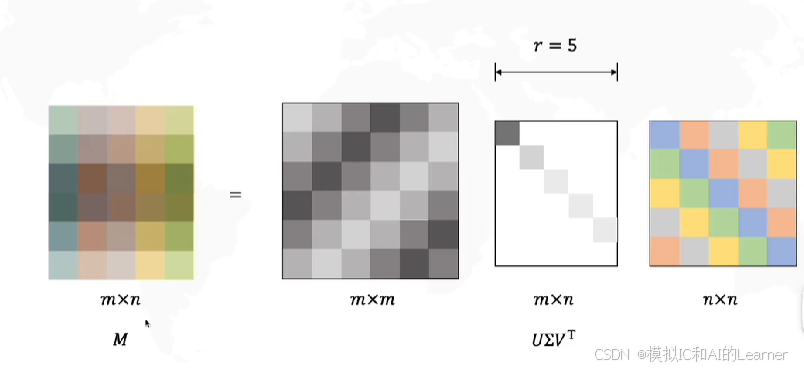
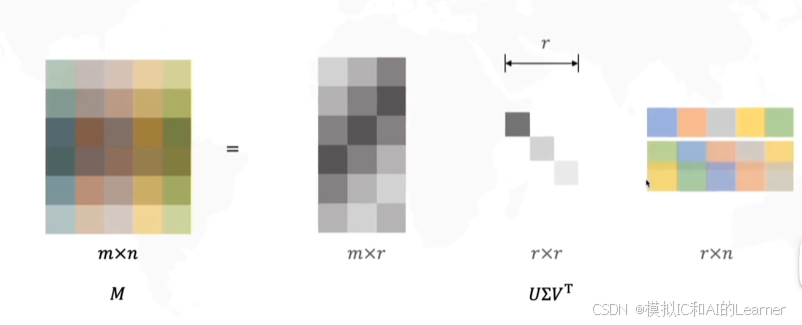
2，第一种“几何解释”，也可以说是SVD的应用。

对于 $\Sigma$ 矩阵，从左到右对角线上的奇异值是逐渐减小的，越往右越小，一些情况下可以去除几维近似：

于是便有了：

乘完之后变成：

最后再相加得到近似的原始矩阵（如果不去掉两个维度，将得到准确的原始矩阵）：

谱分解与奇异值分解的区别

谱分解是以特征向量为中轴，关键点是根据变换前后特征向量的方向没有变化。

奇异值分解可能没有自己的特征向量（或者说没有足够的特征向量），第一次旋转是将右奇异矩阵的特征向量旋转到标准基，然后根据右（或左）奇异矩阵的特征值构成的对角矩阵进行缩放，最后一步与谱分解不同，没有将右奇异矩阵的特征向量旋转回原来的位置，而是根据左奇异矩阵的特征向量旋转（最后一步现还没有清醒的几何解释原因）。

非负矩阵分解

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/117571.html