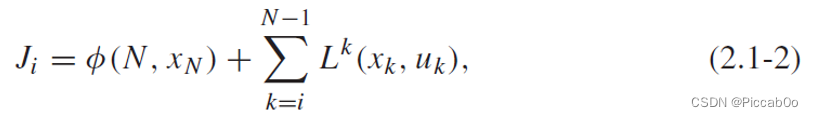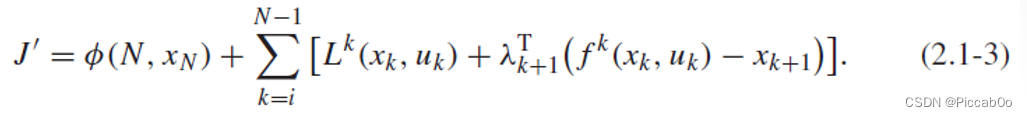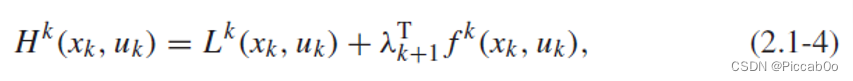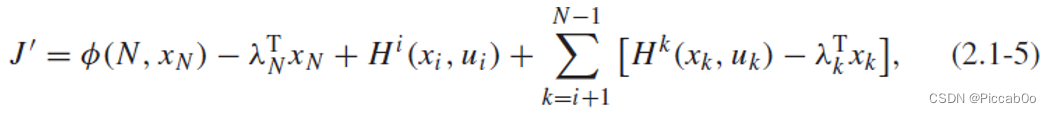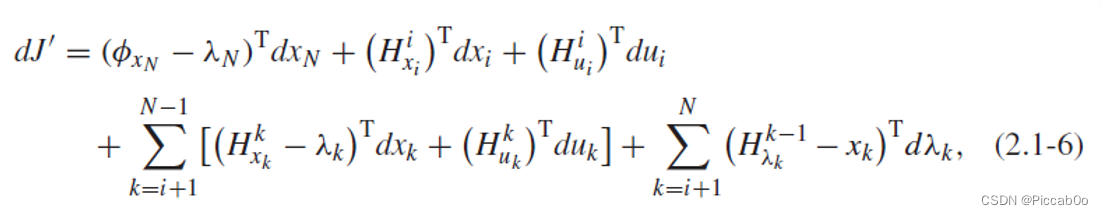【最优控制笔记】——2离散系统最优控制概述

大家好，欢迎来到IT知识分享网。

2.离散系统最优控制

说明：

将前述优化问题推广到动态系统中去，其中的约束$f(x,u)$变成了由系统物理约束等固有条件决定的。

2.1 解决常规离散系统的最优化问题

(1) 目标：

对于一般的离散系统（约束）：

其初态为$x_0$，定义其$[i,N]$时刻内的优化指标为：

(此处的优化指标由自己定义，前半部分是期望达到的目标，后半部分是控制的程度，不同的问题优化指标的设置不同)

最优控制问题是寻找$[i,N]$内的控制$u_k^{\ast }$，使系统沿着轨迹$x_k^{\ast }$让优化指标$J_i$达到最优。

（2）过程：

基于静态优化的思想，对比(2.1-1)所示系统与前述约束，需要给每一个时刻k的约束都设置一个对应的拉格朗日乘子，因此优化指标变成：

引入Hamiltion函数：

则式(2.1-3)变成：

其全微分形式（注意角标变换）为：

当极值点时，应该有$J_{{\lambda }_k}=J_u=J_{x_k}=0$，因此可以得到：

(拉格朗日乘子由系统运动状态定义，故也称伴随系统)

从上式中可以看出求解讨论的基本逻辑：

当$x_N$确定时，用期望的末态值$r_N$作为终端条件；
当$x_N$不确定时，需要终端条件变成${\lambda }_N$。

虽然并不关心协状态${\lambda }_k$的值，但是必须要先求出其才能求出系统的控制$u_k^{\ast }$，进而得知系统的运动状态$x_k^{\ast }$。

（3）举例：

$Pag{e}_{79}-Pag{e}_{91}$举了确定末态值的情况，发现协状态${\lambda }_N$与$r_N-a^N{x}_0$成比例，控制也与之有关（基于离目标的偏差）。

$Pag{e}_{92}-Pag{e}_{99}$举了末态值不固定的情况。