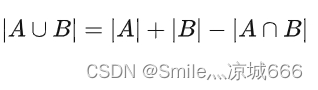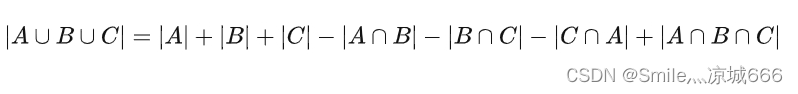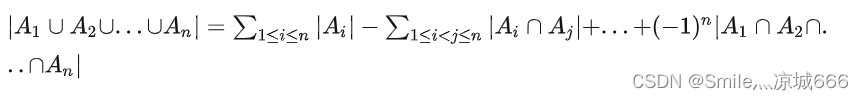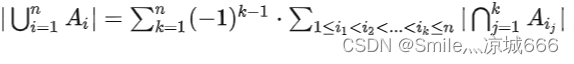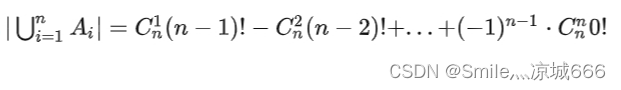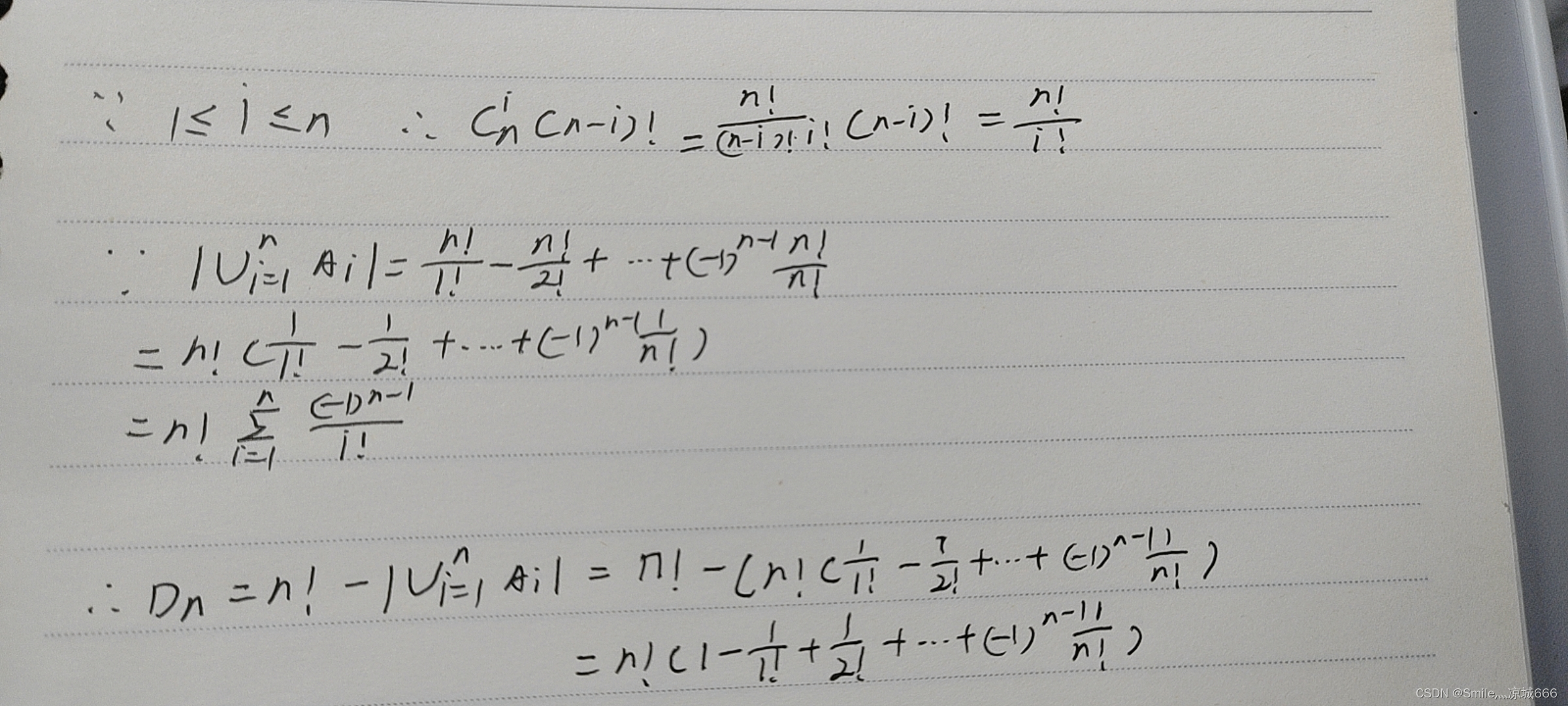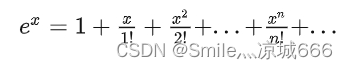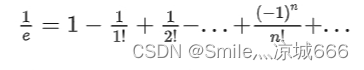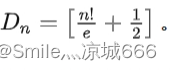错位排序（排列组合）

大家好，欢迎来到IT知识分享网。

一.基础递推式

1.第一种理解方法

当 n≥3 时，考虑  n个元素 a1 ， a2 ， ⋯ ， an ，根据题目要求，我们知道 an 不能放在第

n个位置，所以有（n-1）种选择，假设 an 放在第 i 个位置，考虑元素 ai ，有两种情况。

(1) 若 ai 与 an 调换位置，则只需考虑剩下 n−2 个元素错位全排列的情况。

(2)若 ai 不放在第 n 个位置，则 ai 也无法放在第 i 个位置，因此只需考虑剩下 n−1 个元素错位全排列的情况。

根据加法原理和乘法原理，可以得到： Dn=(n−1)⋅(Dn−1+Dn−2) 。

2.第二种理解方法

假设考虑到第  n个信封，初始时暂时把第 n封信放在第 n 个信封中，然后考虑两种情况的递推：

• 前面 n-1 个信封全部装错；
• 前面 n-1 个信封有一个没有装错其余全部装错。

对于第一种情况，前面  n-1个信封全部装错：因为前面 n-1 个已经全部装错了，所以第 n 封只需要与前面任一一个位置交换即可，总共有(n-1)*Dn-1 种情况。

对于第二种情况，前面 n-1 个信封有一个没有装错其余全部装错：考虑这种情况的目的在于，若n-1 个信封中如果有一个没装错，那么把那个没装错的与 n 交换，也就是剩下n-2个信封排列，总共有（n-1）*Dn-2种。

根据加法原理和乘法原理，可以得到： Dn=(n−1)⋅(Dn−1+Dn−2) 。

（这里也给出另一个递推关系：Dn=nDn-1+()）

二.公式推导

1.n种信封的组合方式有n!种，接下来我们要做的就是扣掉其中重复的种类，保证计数“不重不漏”。

2.容斥原理

（1）两个集合的容斥原理

设有两个非空集A，B，记 |S| 为集合 s 中元素的个数，则有如下关系：

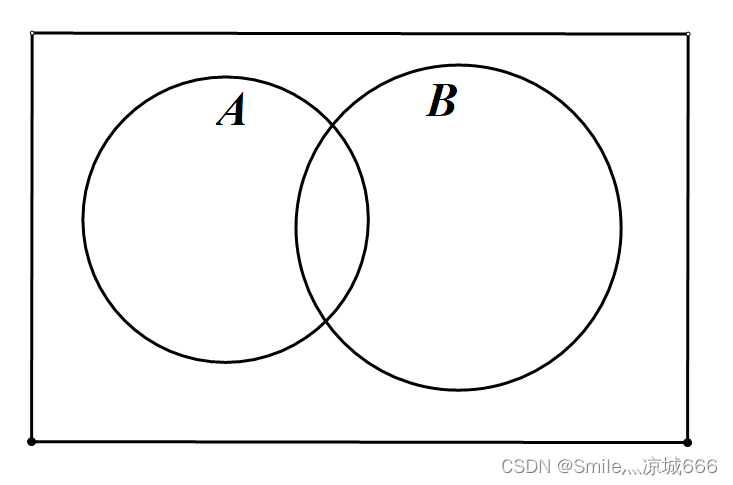
这在文氏图（Venn diagram）中其实是显然的：要计算集合 A∪B 的元素的个数，首先把两集合 A 和 B 的元素个数相加。但是中间出现了重复的部分，也就是集合A∩B 的元素个数，要从中扣除。

(2)三个集合的容斥原理

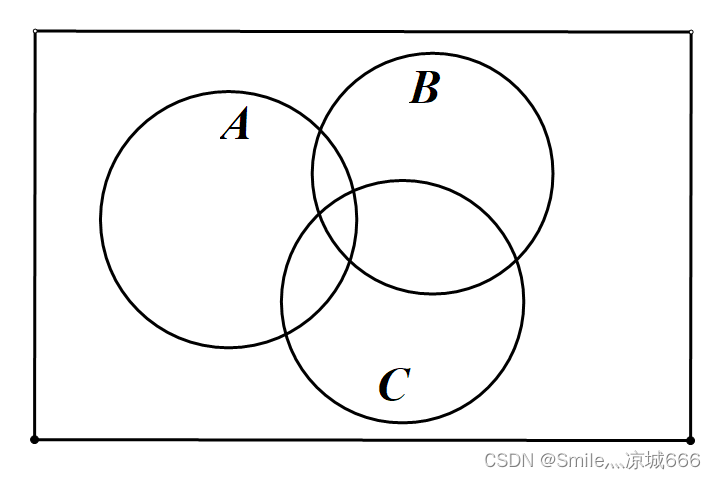
推广到三个集合的情况下，公式要稍加变形：设有三个非空集合 C ，则有如下关系：

（3）多个集合的容斥原理

推广到 n个集合 A1,A2,…,An中，有如下关系：

简化后

此为容斥原理

3.一般计算公式

设元素 a1,a2,…,an 的一个排列为 t1,t2,…,tn，使 ti=ai 的全排列的集合记为 Ai

Dn=n!−| Ai|，接下来只要算出 | Ai|即可。

注意到当有一个元素“排对”时，剩下的 n−1 个元素进行全排列得到 |Ai|=(n−1)! ，并且这样满足要求的集合组共有 =n 个；

当有两个元素“排对”时，剩下 n−2 个元素进行全排列得到 |Ai∩Aj|=(n−2)! ，并且这样满足要求的集合组共有  个；

以此类推，到最后全部“排对”时，|A1∩A2∩…∩An|=0!=1 ，这样满足条件的集合组只有 =1 个。

因此 

从上面我们得到的 Dn 的公式就会发现，为了计算错位全排序，还需要计算多次阶乘。

4.引入级数（Series)与麦克劳林公式

注意到在上面的公式当中，出现了这样的式子： 

 Sn=，我们用计算器来估计一下 Sn 的值。

当 n=3 时， S3=13≈0.3333 ；当 n=5 时， S5=1130≈0.3667 ；

当 n=10 时， S10≈0.3678 。

当 n=50 时， S50≈0. ，取对数得 ln⁡S50≈−1 ，因此 S50≈1/e 。

当n 的值越来越大的时候， Sn 的值也会越来越接近 1/e 。

事实上，在高等数学当中，函数 f(x)= 的麦克劳林公式（Maclaurin’s series）如下：

在原本的公式中，本应该有余项，表示估计的误差大小：

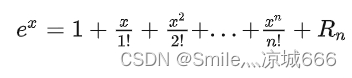
当 n 增大时，余项 Rn趋近于 0 。

把 x = -1 带入 得

因此 Sn 约等于 1 / e;

5.估计公式