Python进阶语法：列表推导式

大家好，欢迎来到IT知识分享网。

1.  什么是列表推导式？

1.1  列表推导式介绍

推导式comprehensions（又称解析式），是Python的一种独有特性，可以从一个数据序列构建另一个新的数据序列。具有使用方便，让代码看起来很高级的功能。

列表推导式是 Python 语言特有的一种语法结构，也可以看成是 Python 中一种独特的数据处理方式。所谓的列表推导式，就是指的轻量级循环创建列表。

1.2  列表推导式的两大作用

它在 Python 中用于 转换 和 过滤 数据。

1.3  列表推导式的语法格式

[表达式 for 迭代变量 in 可迭代对象 [if 条件表达式]]

列表推导式中存在两个名词，一个是 列表，另一个是 推导式 ，

列表我们很清楚，就是 Python 的一种数据类型，而推导式只是一个普通的语法定义词，有的教程里，会将其叫做 解析式，二者是一样的概念。

列表推导式会返回一个列表，因此它适用于所有需要列表的场景。

2.  列表推导式怎么使用？

2.1  数据的转换

2.1.1  优化简单循环

列表推导式最常见的场景就是优化简单循环。

考虑以下需求：

要取出下面列表中的数字，然后平方，再得到一个新的列表。

a=[1,2,3,'a','b','c'] 

一般可以这样解决：

# 定义一个列表a，包含整数和字符串 a = [1, 2, 3, 'a', 'b', 'c'] # 定义一个空列表b，用于存放满足条件的元素 b = [] # 遍历列表a中的每一个元素 for i in a: # 使用isinstance（a,type）函数判断当前元素i是否是整数类型，如果是整数类型，则进入if语句块 if isinstance(i, int): # 将当前整数元素i进行平方操作 b.append(i 2) # 打印列表b的内容 print(b) # 返回结果：[1,4,9] 

如果使用列表推导式，会简洁很多：

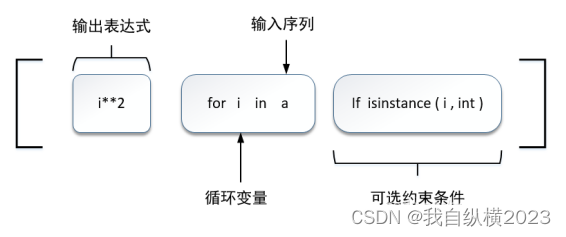
a = [1, 2, 3, 'a', 'b', 'c'] b = [i2 for i in a if isinstance(i,int)] print(b)

列表表达式由四个部分组成：

• 输入的列表
• 列表循环变量
• 可选的约束条件
• 输出表达式

列表推导式最终会将得到的各个结果组成一个新的列表。

2.1.2  优化两层 for 循环

列表推导式能支持两层 for 循环，例如下述代码：

a = [1,2,3,4,5,6,7] b = [1,2,3,4,7,7,7] c = [(x,y) for x in a for y in b if(x==y)] print(c) # 返回：[(1, 1), (2, 2), (3, 3), (4, 4), (7, 7), (7, 7), (7, 7)]

上述代码相当于下面的两层 for 循环：

a = [1, 2, 3, 4, 5, 6, 7] b = [1, 2, 3, 4, 7, 7, 7] c = [] for x in a: for y in b: if x == y: c.append((x, y)) print(c)

代码运行步骤： 

1. 先遍历 a 列表的第一个元素：x=1
2. 再分别遍历 b 列表中的每一个元素：y=1、2、3、4、5、6、7
3. 检查 x 和 y 是否相等？得到：(1,1)
4. 再次按前三个步骤循环，依次得到：(2,2) (3,3) (4,4) (7,7) (7,7) (7,7)
5. 最后把得到的元组添加到列表 c 里面。

如果想要得到 a、b 两个列表中对应索引相同的元素对，代码如下：

a = [1,2,3,4,5,6,7] b = [1,2,3,4,7,7,7] d = [(a[x],b[y]) for x in range(7) for y in range(7) if a[x]==b[y]and(x==y)] print(d) # 返回：[(1, 1), (2, 2), (3, 3), (4, 4), (7, 7)]

 代码的核心是一个嵌套的列表推导式，它生成一个元组列表d。这个列表推导式遍历a和b的所有索引（从0到6），并检查a[x]是否等于b[y]，并且x是否等于y。如果这两个条件都满足，那么它就将一个元组添加到列表d中。

这里是代码的逐步解释：

1. for x in range(7) for y in range(7): 这部分是嵌套循环，它遍历两个列表的所有索引。
2. if a[x]==b[y]: 这部分检查a在索引x处的元素是否等于b在索引y处的元素。
3. and (x==y): 这部分确保我们只考虑那些索引相等的元素。
4. (a[x],b[y]): 这部分创建一个元组，其中包含从两个列表中取出的元素。

当然如果你想加密（谁都看不懂你的代码）你的代码，你可以无限套娃下去，列表推导式并没有限制循环层数，多层循环就是一层一层的嵌套，你可以展开一个三层的列表推导式，就都明白了

nn_list = [(x,y,z,m) for x in range(3) for y in range(3) for z in range(3) for m in range(3)] print(nn_list)

 当然在多层列表推导式里面，依旧支持 if 语句，并且 if 后面可以用前面所有迭代产生的变量，不过不建议超过 2 成，超过之后会大幅度降低你代码的可阅读性。

当然如果你希望你代码更加难读，下面的写法都是正确的。

nn_list = [(x, y, z, m) for x in range(3) if x > 1 for y in range(3) if y > 1 for z in range(3) for m in range(3)] print(nn_list) nn_list = [(x, y, z, m) for x in range(3) for y in range(3) for z in range(3) for m in range(3) if x > 1 and y > 1] print(nn_list) nn_list = [(x, y, z, m) for x in range(3) for y in range(3) for z in range(3) for m in range(3) if x > 1 if y > 1] print(nn_list)

有了两种不同的写法，那咱们必须要对比一下效率，经测试小数据范围影响不大，当循环次数到千万级时候，出现了一些差异。

# 导入时间模块，用于测量代码运行时间 import time # 定义一个名为demo1的函数，该函数创建一个新的空列表，并使用for循环逐个添加元素 def demo1(): new_list = [] # 初始化一个空列表new_list for i in range(): # 使用for循环遍历0到的整数 new_list.append(i * 2) # 将当前i的二倍值添加到new_list中 # 定义一个名为demo2的函数，该函数使用列表推导式创建一个新列表 def demo2(): new_list = [i * 2 for i in range()] # 使用列表推导式创建新列表，列表中的每个元素是i的二倍，其中i从0到 # time.perf_counter() 返回系统当前运行时间 # 记录当前时间作为开始时间点 s_time1 = time.perf_counter() # 调用demo2函数并执行，但不记录时间，因为后续会单独测量该函数的时间 demo1() # 记录当前时间作为结束时间点，并计算demo2函数的运行时间 e_time1 = time.perf_counter() print('demo1运行时间：',e_time1-s_time1) s_time2 = time.perf_counter() demo2() e_time2 = time.perf_counter() print('demo2运行时间：',e_time2-s_time2) # for 循环(demo1):demo1运行时间： 0. # 列表推导式(demo2):demo2运行时间： 0.

2.1.3  矩阵按列读取

a = [[1,2,3],[4,5,6],[7,8,9]] b = [[row[i] for row in a] for i in range(3)] print(b) # 返回： 

上面的列表推导式相当于下面的二层 for 循环：

a = [[1,2,3],[4,5,6],[7,8,9]] c = [] for i in range(3): temp_list = [] for row in a: temp_list.append(row[i]) print(row) c.append(temp_list) print(c)

2.1.4  实现嵌套列表的平铺

列表推导式还支持嵌套

示例：

vec = [[1,2,3],[4,5,6],[7,8,9]] print(vec) # [[1, 2, 3], [4, 5, 6], [7, 8, 9]] y = [j for i in vec for j in i] print(y) # [1, 2, 3, 4, 5, 6, 7, 8, 9] 

my_var = [y*4 for y in [x*2 for x in range(3)]] print(my_var) # [0, 8, 16]

2.2  数据的过滤

2.2.1  过滤不符合条件的元素

my_list = [1, 2, 3] new_list = [item for item in my_list if item > 1] print(new_list) # [2,3]

2.2.2 生成100以内的素数

试除法：通过尝试将n除以2到sqrt(n)之间的所有整数，如果都无法整除，则n是素数。具体步骤如下：

• 从2开始，遍历2到sqrt(n)的所有整数，尝试将n除以当前整数。
• 如果n能够被当前整数整除，则n不是素数。
• 如果遍历完所有整数后都没有找到能够整除n的数，则n是素数。

import numpy as np a = [x for x in range(2,101) if 0 not in [x%i for i in range(2,int(np.sqrt(x)))] ] print(a) 

这段代码使用了numpy库和列表推导式。它的目的是找出2到100（包含100）之间所有质数。

让我们逐步解释这段代码：

1. import numpy as np: 导入numpy库，并用缩写np表示。
2. a = [x for x in range(2,101) if 0 not in [x%i for i in range(2,int(np.sqrt(x)))] ]: 这是一个列表推导式，用于生成一个新列表a。
   • for x in range(2,101): 对于2到100之间的每个数字x，都执行以下的条件判断。
   • if 0 not in [x%i for i in range(2,int(np.sqrt(x)))]: 这是条件判断部分。它检查数字x是否是质数。
     • for i in range(2,int(np.sqrt(x))): 对于每个数字i从2到x的平方根（不包括平方根，因为一个大于平方根的因数必定有一个小于平方根的对应因数），执行以下操作。
     • x%i: 求x除以i的余数。
     • x%i == 0: 如果余数为0，那么i是x的一个因数。
     • 0 not in [x%i for i in range(2,int(np.sqrt(x)))]: 如果0不在这个列表中，那么这个列表只包含非零元素，意味着x没有小于或等于其平方根的因数，因此x是一个质数。
3. print(a): 打印列表a。

最终，这段代码将打印出2到100之间的所有质数。