大家好,欢迎来到IT知识分享网。
目录
一.决策树
- 特征选择:根据某个准则(如信息增益、基尼不纯度等),选择最佳的特征作为当前节点的划分属性。
- 树的生成:递归地将数据集划分为子集,直到数据集中的所有样本属于同一类别或满足停止条件。
- 剪枝:为了避免过拟合,可以对生成的树进行剪枝操作,去除一些不必要的节点或分支。
决策树具有易于理解和解释的优点,同时适用于分类和回归任务,并且能够处理非线性关系和缺失值。然而,决策树也容易过拟合训练数据,特别是当树的深度过大或训练样本数量不足时。
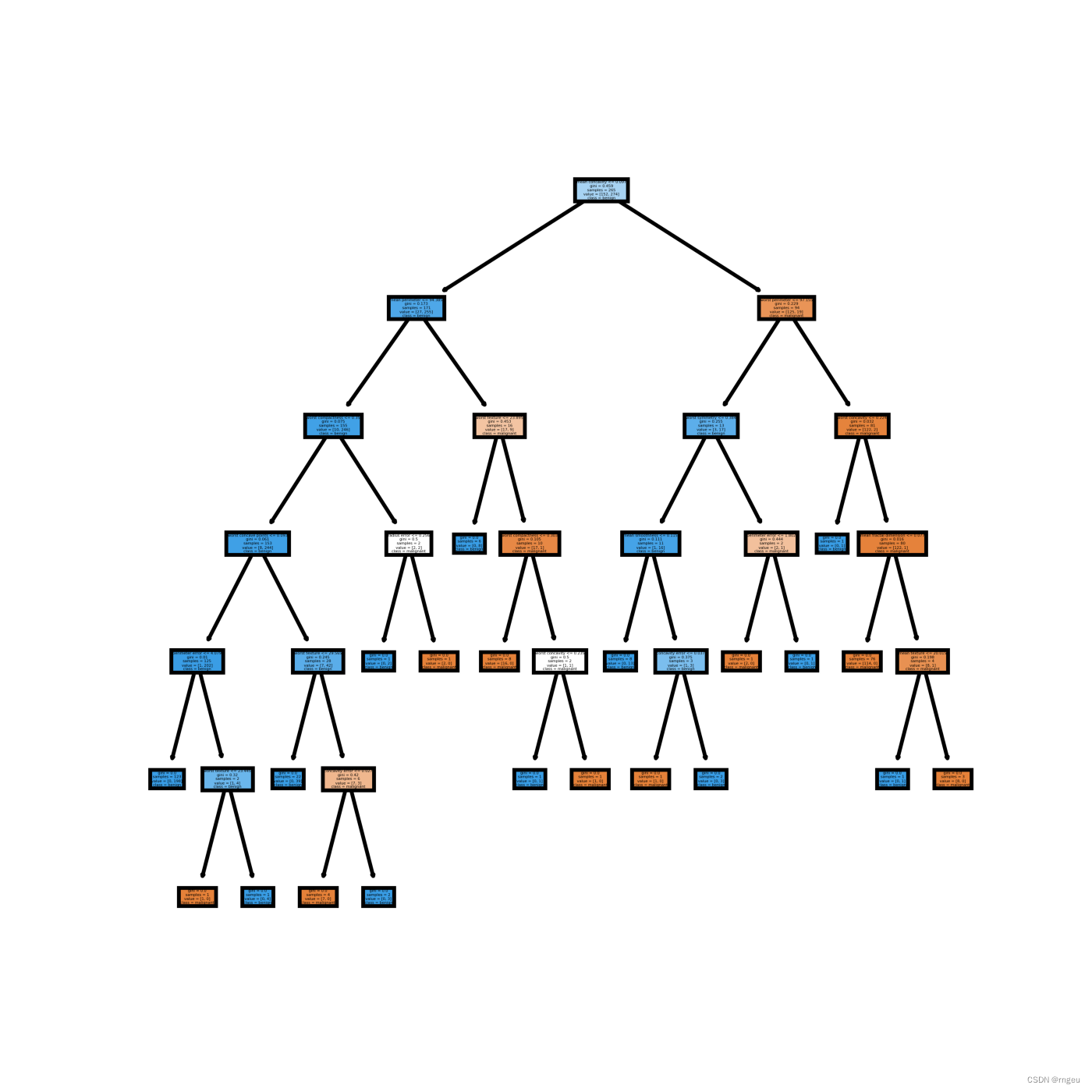
上图为决策树示意图,圆点——内部节点,方框——叶节点
决策树学习的目标:根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
- 决策树学习的本质:从训练集中归纳出一组分类规则,或者说是由训练数据集估计条件概率模型。
- 决策树学习的损失函数:正则化的极大似然函数
- 决策树学习的测试:最小化损失函数
- 决策树学习的目标:在损失函数的意义下,选择最优决策树的问题。
- 决策树原理和问答猜测结果游戏相似,根据一系列数据,然后给出游戏的答案。
1.决策树的特征选择
1.1信息增益
熵 – 条件熵。信息增益代表了在一个条件下,信息不确定性减少的程度。
划分数据集的大原则是:将无序数据变得更加有序,但是各种方法都有各自的优缺点,信息论是量化处理信息的分支科学,在划分数据集前后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择,所以必须先学习如何计算信息增益,集合信息的度量方式称为香农熵,或者简称熵。
为了计算熵,我们需要计算所有类别所有可能值所包含的信息期望值,通过下式得到:
1.2熵
表示随机变量的不确定性。
在决策树中,熵越高表示数据集的不确定性越大,即数据集中包含的不同类别的样本数量相对均衡,难以进行有效的划分;而熵越低表示数据集的纯度越高,即数据集中的样本大部分属于同一类别,易于进行划分。
2.决策树的生成
2.1ID3算法
ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,即Iterative Dichotomiser 3,迭代二叉树3代,是Ross Quinlan发明的一种决策树算法,这个算法的基础就是上面提到的奥卡姆剃刀原理,越是小型的决策树越优于大的决策树,尽管如此,也不总是生成最小的树型结构,而是一个启发式算法。
已知
则总信息熵为
特征条件下的条件熵
特征的信息增益
需要注意的是,ID3算法可能会存在过度拟合(overfitting)的问题,特别是当训练数据集中存在噪声或特征取值较多时。此外,ID3算法只能处理离散型特征,对于连续型特征需要进行离散化处理或使用其他算法
2.2C4.5算法
C4.5算法与ID3相似,在ID3的基础上进行了改进,采用信息增益比来选择属性。ID3选择属性用的是子树的信息增益,ID3使用的是熵(entropy, 熵是一种不纯度度量准则),也就是熵的变化值,而C4.5用的是信息增益率。
在ID3的计算基础上增添两步
选择最大的信息增益率作为划分
2.3CART算法
CART算法是给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树,内部节点取值为“是”或“否”。这样的决策树等价于递归地二分每个特征,将特征空间划分为有限个单元,并在这些单元上确定预测的概率分布即输入给定的条件下输出的条件概率分布。
特征选择:Gini指数
对于二分类问题,若样本点属于第1个类的概率为p,则概率分布的基尼指数为
计算每一个特征的Gini指数
基尼指数G i n i ( D ) Gini(D)Gini(D)表示集合D的不确定性,基尼指数G i n i ( D , A ) Gini(D,A)Gini(D,A)表示经A = a A=aA=a分割后集合D的不确定性。基尼系数越大,样本集合的不确定性也越大,这一点与熵相似。
需要选择Gini指数小的特征进行划分
3.决策树的剪枝
3.1原理
决策树剪枝是一种用于减小决策树复杂度、防止过拟合的技术。其原理是在已经生成的决策树上进行修剪,删除一些节点或子树,以达到降低模型复杂度、提高泛化能力的目的。下面是决策树剪枝的主要原理:
- 预剪枝(Pre-pruning):在决策树生成过程中,在每个节点划分前进行评估,如果划分后无法提高模型的泛化能力,就停止该节点的划分,将当前节点标记为叶子节点。预剪枝的优点是简单且易于实现,但可能会过早停止树的生长,导致欠拟合。
- 后剪枝(Post-pruning):后剪枝是在生成完整决策树后,从底部向上逐步移除节点或子树。具体做法是将子树替换为单个叶子节点,然后使用验证集或交叉验证对修剪后的树进行评估,如果修剪后的树性能有所提升,则保留修剪操作,否则恢复之前的状态。后剪枝相对于预剪枝来说,更加灵活,能够在生成完整树后根据实际情况进行剪枝,避免了预剪枝可能带来的欠拟合问题。
- 剪枝标准(Pruning Criteria):在进行剪枝时,需要定义一个评价准则来判断剪枝操作是否合理。常见的剪枝标准包括错误率(Misclassification Rate)、基尼指数(Gini Index)、信息增益(Information Gain)等。剪枝标准的选择取决于具体的任务和数据集。
- 剪枝策略(Pruning Strategies):在决策树剪枝过程中,通常会使用一些策略来确定剪枝的顺序和方式,常见的策略包括悲观剪枝(Pessimistic Pruning)、悲观剪枝(Optimistic Pruning)等。
3.2算法思路
- 生成完整的决策树:首先,利用训练数据生成完整的决策树,即不进行任何剪枝操作,直到每个叶子节点都包含一个纯度较高的类别或达到停止条件(如达到最大深度)为止。
- 后剪枝:从底部向上遍历决策树的每个节点或子树。将当前节点或子树替换为单个叶子节点,并计算修剪后的树在验证集或交叉验证上的性能。如果修剪后的树性能有所提升,则保留修剪操作,否则恢复之前的状态。重复以上步骤,直到无法再进行剪枝为止。
- 剪枝标准和策略:在剪枝过程中,需要选择合适的剪枝标准和剪枝策略,例如基于错误率、基尼指数或信息增益等来评估修剪后的树性能,并采用悲观剪枝或乐观剪枝等策略确定剪枝顺序和方式。
4.实例实现
4.1ID3
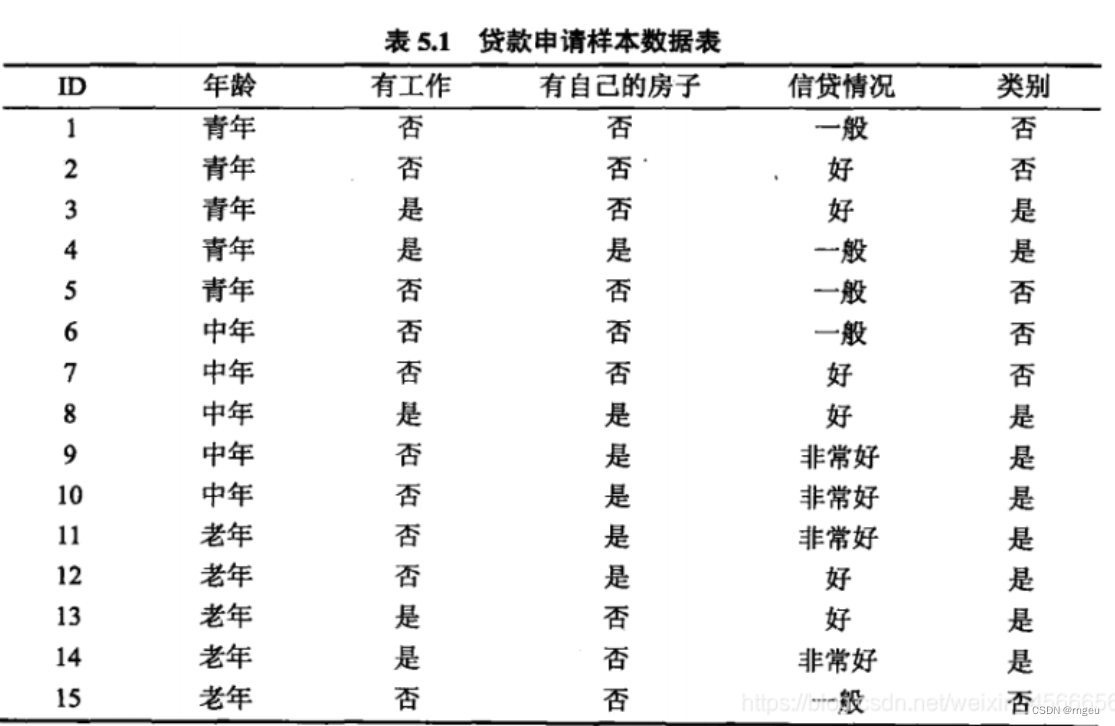
案例介绍
创建数据集
def create_data(): datasets = [['青年', '否', '否', '一般', '否'], ['青年', '否', '否', '好', '否'], ['青年', '是', '否', '好', '是'], ['青年', '是', '是', '一般', '是'], ['青年', '否', '否', '一般', '否'], ['中年', '否', '否', '一般', '否'], ['中年', '否', '否', '好', '否'], ['中年', '是', '是', '好', '是'], ['中年', '否', '是', '非常好', '是'], ['中年', '否', '是', '非常好', '是'], ['老年', '否', '是', '非常好', '是'], ['老年', '否', '是', '好', '是'], ['老年', '是', '否', '好', '是'], ['老年', '是', '否', '非常好', '是'], ['老年', '否', '否', '一般', '否'], ] labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别'] # 返回数据集和每个维度的名称 return datasets, labels 构建决策树
def single_ent(datasets,j): data_length = len(datasets)#返回数据集的行数即样本个数 label_count = {}#保存每个标签(Label)出现次数的字典 for i in range(data_length): label = datasets[i][j]#数据集的最后一列 if label not in label_count:#如果标签(Label)没有放入统计次数的字典,添加进去 label_count[label] = 0 label_count[label] += 1#Label计数 ent = -sum([(p / data_length) * log(p / data_length, 2)#计算经验熵 for p in label_count.values()]) return ent#返回经验熵 """ 函数说明:计算各个特征对于训练集的条件经验熵 Parameters: datasets - 数据集 j - 数据集第j列即特征值索引 Returns: cond_ent - 条件经验熵(香农熵) """ # 经验条件熵$ H(D|A)$ def cond_ent(datasets, j):#参数j:指定特征 data_length = len(datasets) feature_sets = {} for i in range(data_length): feature = datasets[i][j] if feature not in feature_sets:#如果特征没有放入统计次数的字典,添加进去 feature_sets[feature] = [] feature_sets[feature].append(datasets[i])#划分数据集 cond_ent = sum( [(len(p) / data_length) * single_ent(p,-1) for p in feature_sets.values()]) return cond_ent """ 函数说明:计算某特征对于训练集的信息增益 Parameters: datasets - 数据集 j - 数据集第j列即特征值索引 Returns:信息增益 """ # 信息增益 def info_gain(datasets, j): return single_ent(datasets,-1)-cond_ent(datasets,j) """ 函数说明:计算某特征对于训练集的信息增益比 Parameters: datasets - 数据集 j - 数据集第j列即特征值索引 Returns:信息增益比 """ # 信息增益比 def info_gain_ratio(datasets,j): return 0 if single_ent(datasets,j)==0 else info_gain(datasets,j)/single_ent(datasets,j) """ 函数说明:选取最有特征 Parameters: datasets - 数据集 method-选择最优特征准则:ID3:依据信息增益;C4.5:依据信息增益比 Returns: bestFeature - 信息增益最大的(最优)特征的索引值 """ def bestfeature(datasets,method='ID3'): assert method in ['ID3','C4.5'],"method 须为id3或c45" def calcEnt(datasets,j): if method=='ID3': return info_gain(datasets,j) if method=='C4.5': return info_gain_ratio(datasets,j) count = len(datasets[0]) - 1 #特征数量 features = [] #记录各个特征的信息增益 for c in range(count): c_info_gain = calcEnt(datasets,c)#信息增益 features.append((c, c_info_gain)) #print('特征({}) - 信息增益 - {:.3f}'.format(labels[c], c_info_gain)) # 比较大小 best_ = max(features, key=lambda x: x[-1]) bestFeature=best_[0] return bestFeature """ 函数说明:统计classList中出现最多的类标签 Parameters: classList - 类标签列表 Returns: sortedClassCount[0][0] - 出现此处最多的元素(类标签) """ def majorityCnt(classList): classCount = {} for vote in classList: #统计classList中每个元素出现的次数 if vote not in classCount.keys():classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True) #根据字典的值降序排序 return sortedClassCount[0][0] #返回classList中出现次数最多的元素 """ 函数说明:按照给定特征划分数据集 Parameters: datasets - 待划分的数据集 axis - 划分数据集的特征 value - 需要删除的特征的值 Returns: 无 """ def splitDataSet(datasets, axis, value): retDataset = [] #创建返回的数据集列表 for featVec in datasets: #遍历数据集 if featVec[axis] == value: reducedFeatVec = featVec[:axis] #去掉axis特征 reducedFeatVec.extend(featVec[axis+1:]) #将符合条件的添加到返回的数据集 retDataset.append(reducedFeatVec) return retDataset #返回划分后的数据集 """ 函数说明:创建决策树 Parameters: datasets - 训练数据集 labels - 分类属性标签 featLabels - 存储选择的最优特征标签 Returns: myTree - 决策树 """ def createTree(datasets, labels, featLabels): classList = [example[-1] for example in datasets] #取分类标签(是否放贷:yes or no) if classList.count(classList[0]) == len(classList): #1、如果类别完全相同则停止继续划分 return classList[0] if len(datasets[0]) == 1: #2、如果特征集为空即数据集只有1列 return majorityCnt(classList) #遍历完所有特征时返回出现次数最多的类标签 bestFeat = bestfeature(datasets,method='ID3') #3、选择最优特征,方法可以更改 bestFeatLabel = labels[bestFeat] #最优特征的标签 featLabels.append(bestFeatLabel) myTree = {bestFeatLabel:{}} #根据最优特征的标签生成树 del(labels[bestFeat]) # 已经选择的特征不再参与分类 featValues = [example[bestFeat] for example in datasets] #得到训练集中所有最优特征的属性值 uniqueVals = set(featValues) #去掉重复的属性值 for value in uniqueVals: #遍历特征,创建决策树。 myTree[bestFeatLabel][value] = createTree(splitDataSet(datasets, bestFeat, value), labels, featLabels) return myTree 决策可视化
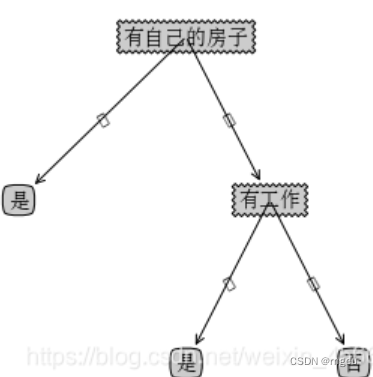
""" 函数说明:获取决策树叶子结点的数目 Parameters: myTree - 决策树 Returns: numLeafs - 决策树的叶子结点的数目 """ def getNumLeafs(myTree): numLeafs = 0 #初始化叶子 firstStr = next(iter(myTree)) #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0] secondDict = myTree[firstStr] #获取下一组字典 for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict': #测试该结点是否为字典,如果不是字典,代表此结点为叶子结点 numLeafs += getNumLeafs(secondDict[key]) else: numLeafs +=1 return numLeafs """ 函数说明:获取决策树的层数 Parameters: myTree - 决策树 Returns: maxDepth - 决策树的层数 """ def getTreeDepth(myTree): maxDepth = 0 #初始化决策树深度 firstStr = next(iter(myTree)) #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0] secondDict = myTree[firstStr] #获取下一个字典 for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict': #测试该结点是否为字典,如果不是字典,代表此结点为叶子结点 thisDepth = 1 + getTreeDepth(secondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth #更新层数 return maxDepth """ 函数说明:绘制结点 Parameters: nodeTxt - 结点名 centerPt - 文本位置 parentPt - 标注的箭头位置 nodeType - 结点格式 Returns: 无 """ def plotNode(nodeTxt, centerPt, parentPt, nodeType): arrow_args = dict(arrowstyle="<-") #定义箭头格式 font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14) #设置中文字体 createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', #绘制结点 xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, FontProperties=font) """ 函数说明:标注有向边属性值 Parameters: cntrPt、parentPt - 用于计算标注位置 txtString - 标注的内容 Returns: 无 """ def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] #计算标注位置 yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) """ 函数说明:绘制决策树 Parameters: myTree - 决策树(字典) parentPt - 标注的内容 nodeTxt - 结点名 Returns: 无 """ def plotTree(myTree, parentPt, nodeTxt): decisionNode = dict(boxstyle="sawtooth", fc="0.8") #设置结点格式 leafNode = dict(boxstyle="round4", fc="0.8") #设置叶结点格式 numLeafs = getNumLeafs(myTree) #获取决策树叶结点数目,决定了树的宽度 depth = getTreeDepth(myTree) #获取决策树层数 firstStr = next(iter(myTree)) #下个字典 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) #中心位置 plotMidText(cntrPt, parentPt, nodeTxt) #标注有向边属性值 plotNode(firstStr, cntrPt, parentPt, decisionNode) #绘制结点 secondDict = myTree[firstStr] #下一个字典,也就是继续绘制子结点 plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD #y偏移 for key in secondDict.keys(): if type(secondDict[key]).__name__=='dict': #测试该结点是否为字典,如果不是字典,代表此结点为叶子结点 plotTree(secondDict[key],cntrPt,str(key)) #不是叶结点,递归调用继续绘制 else: #如果是叶结点,绘制叶结点,并标注有向边属性值 plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD """ 函数说明:创建绘制面板 Parameters: inTree - 决策树(字典) Returns: 无 """ def createPlot(inTree): fig = plt.figure(1, facecolor='white') #创建fig fig.clf() #清空fig axprops = dict(xticks=[], yticks=[]) createPlot.ax1 = plt.subplot(111, frameon=False, axprops) #去掉x、y轴 plotTree.totalW = float(getNumLeafs(inTree)) #获取决策树叶结点数目 plotTree.totalD = float(getTreeDepth(inTree)) #获取决策树层数 plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0; #x偏移 plotTree(inTree, (0.5,1.0), '') #绘制决策树 plt.show() #显示绘制结果 运行结果
{'有自己的房子': {'否': {'有工作': {'否': '否', '是': '是'}}, '是': '是'}}4.2CART
案例介绍
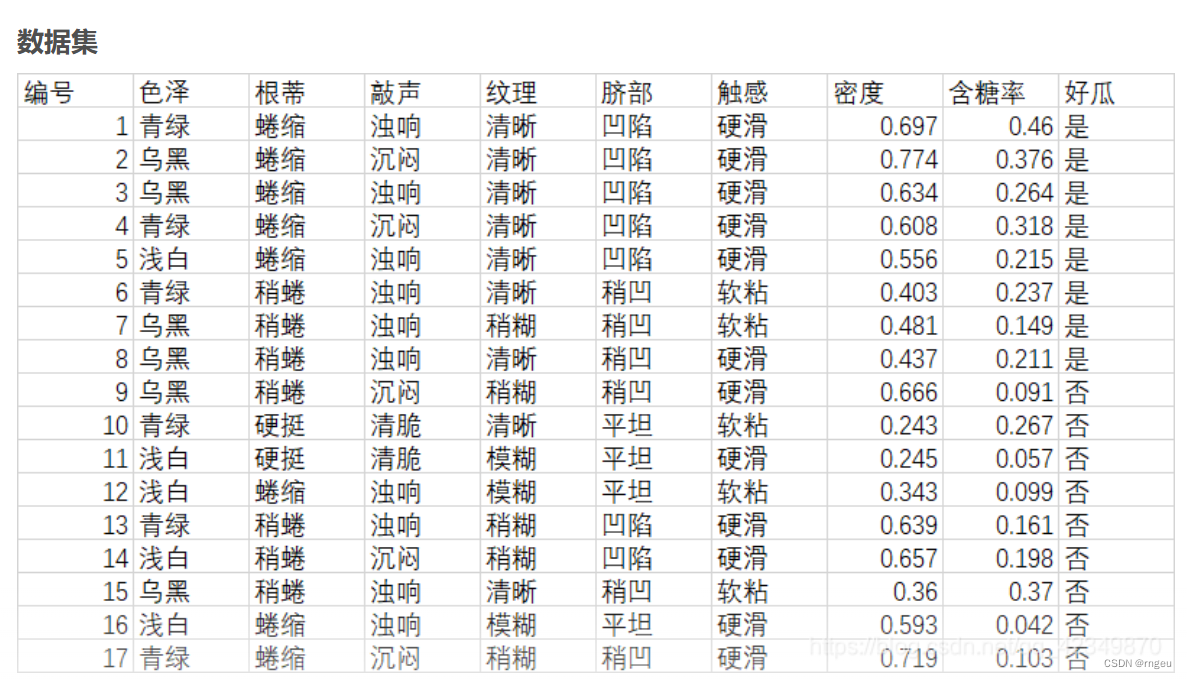
数据集采用周志华《机器学习》课后习题4.3的西瓜数据集
创建数据集
D = [ ['青绿','蜷缩','浊响','清晰','凹陷','硬滑','是'], ['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','是'], ['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','是'], ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','是'], ['浅白','蜷缩','浊响','清晰','凹陷','硬滑','是'], ['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'], ['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'], ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'], ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否'], ['青绿','硬挺','清脆','清晰','平坦','软粘','否'], ['浅白','硬挺','清脆','模糊','平坦','硬滑','否'], ['浅白','蜷缩','浊响','模糊','平坦','软粘','否'], ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','否'], ['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','否'], ['乌黑','稍蜷','浊响','清晰','稍凹','软粘','否'], ['浅白','蜷缩','浊响','模糊','平坦','硬滑','否'], ['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','否'] ] A = ['色泽','根蒂','敲声','纹理','脐部','触感','好瓜']
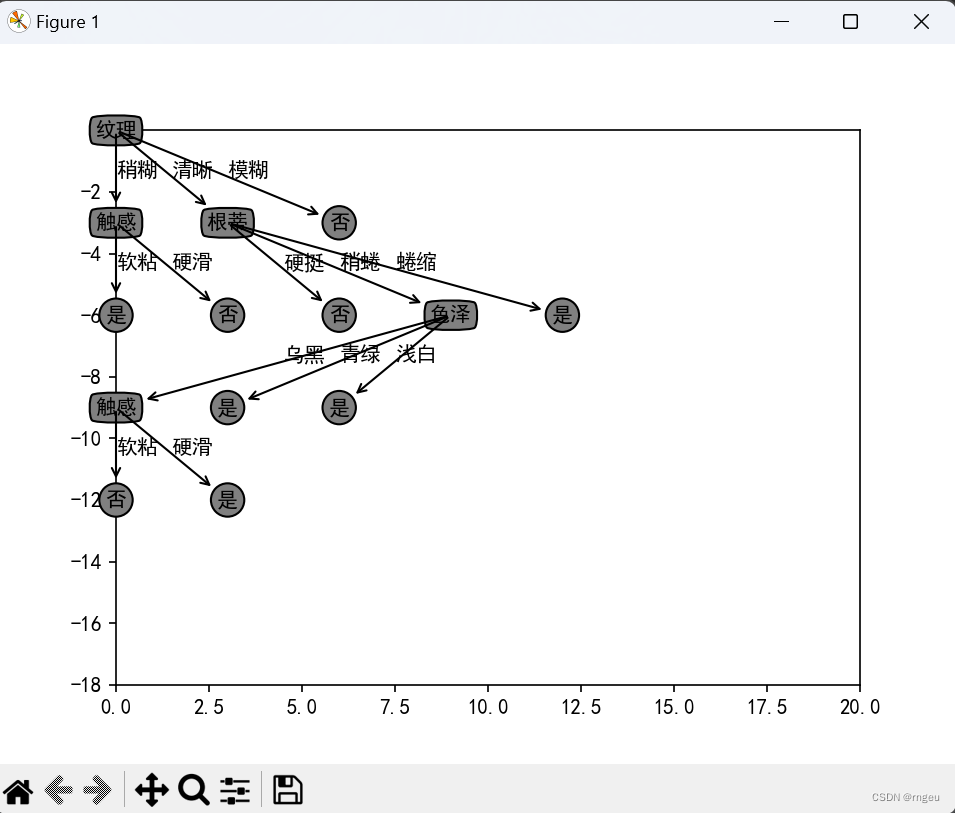
class Cart: # 数据 data = None # 属性集合 attributes = None # 属性集合 (与下标关系),去除最后的类型判定列 attributesAndIndex = None # 属性下标 (与属性可能的取值),去除最后的类型判定列 attributesIndexAndValue = None # 根节点 root = None def __init__(self,data,attributes): self.data = data self.attributes = attributes self.attributesAndIndex = Cart.getAttributesAndIndex(attributes) self.attributesIndexAndValue = Cart.getAttributesAndValue(data,attributes) def draw(self): self.createTree(self.root,self.data,self.attributesAndIndex,None) tree = Tree(self.root) tree.drawTree() # attributesAndIndex 不是类的那个属性了,这个引用会在递归的过程中长度被削减 def createTree(self,node,data,attributesAndIndex,desc): # 创建节点 newNode = Node() # 如果传入了desc,写入 if(desc is not None): newNode.desc = desc if node is None: self.root = newNode else: node.addChild(newNode) # 如果data中的样本属于同一类别,那么将newNode标记为C类叶节点.返回 kMap = Cart.getKMap(data) if len(kMap) == 1: newNode.name = next(iter(kMap.keys())) return # 如果属性列表是空集,或D在A上的取值相同 if Cart.checkDA(data,attributesAndIndex): # 获取数据集中较多的那个类别 newNode.name = Cart.getMoreType(data) return # 获取最优属性下标 bestIndex = Cart.getMinGiniIndexStrict(data,attributesAndIndex) newNode.name = self.attributes[bestIndex] # 遍历最优属性的每一个属性值(从原始数据中) aStart = self.attributesIndexAndValue[bestIndex] # 按最优属性拆分数据,为多个子集 V = Cart.splitDataByIndex(data,bestIndex) for aStartV in aStart: dv = V.get(aStartV) # 如果dv是空集,那么以获取数据集中较多的那个类别建立子节点 if dv is None or len(dv) == 0: newLeaf = Node() newLeaf.name = Cart.getMoreType(data) newLeaf.desc = aStartV newNode.addChild(newLeaf) else: # 将A抛去选中的那个 Anew = copy.deepcopy(attributesAndIndex) for index,item in enumerate(Anew): if next(iter(item.values())) == bestIndex: Anew.pop(index) break self.createTree(newNode,dv,Anew,aStartV) # 检查D在a上的取值是否完全相同(data的所有数据不一定类别完全相同,只要在a上(可能多个)的取值完全相同即可) # 也就是指定类型的那些属性值完全一致,例如下文中的根蒂,脐部.在data上均没有区别都是稍蜷和稍凹 # 例如 A['根蒂','脐部'] D : #['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'], #['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'], #['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'], #['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否'], @staticmethod def checkDA(data,attributesAndIndex): if len(attributesAndIndex) == 0: return True for item in attributesAndIndex: # 当前的属性值 nowAttributesValue = None # 获取属性下标 i aIndex = next(iter(item.values())) for dLine in data: if nowAttributesValue == None: nowAttributesValue = dLine[aIndex] elif nowAttributesValue != dLine[aIndex]: return False return True; # 将属性附加一个指向数据的哪一个列,删除最后的类别信息,只保留属性信息 # ['色泽','根蒂'] -> [{'色泽':0},{'根蒂':1}] @staticmethod def getAttributesAndIndex(attributes): attributesAndIndex = list() for index,attribute in enumerate(attributes): attributesAndIndex.append({attribute:index}) return attributesAndIndex[:len(attributesAndIndex) - 1] @staticmethod def getAttributesAndValue(data,attributes): attributesAndValue = dict() for dLine in data: for i in range(len(attributes) - 1): v = attributesAndValue.get(i) if v == None: v = set() attributesAndValue[i] = v v.add(dLine[i]) return attributesAndValue # 获取data数据集中,基尼指数最小的那个属性的下标, # attributesAndIndex的不需要维度必须和data[]的维度一致.使用attributesAndIndex指定的下标查询.不忽略最后一个 @staticmethod def getMinGiniIndexStrict(data,attributesAndIndex): minGiniIndex = None minIndex = None for item in attributesAndIndex: # 获取属性名 v ,属性下标 i aName = next(iter(item.keys())) aIndex = next(iter(item.values())) giniIndex = Cart.getGiniIndex(data,aIndex) if minGiniIndex == None or giniIndex < minGiniIndex: minGiniIndex = giniIndex minIndex = aIndex print("第" , aIndex ,"列的属性",aName,"的基尼指数为:" , giniIndex) print("第" , minIndex ,"列的属性",aName,"的基尼指数最小为:" , minGiniIndex ,";为最优划分属性") return minIndex # 获取data数据集中,基尼指数最小的那个属性的下标,attributes的维度必须和data[]的维度一致 @staticmethod def getMinGiniIndex(data,attributes): # attributes 的最后一列是类别,不计入 attributesSize = len(attributes) - 1 i = 0 minGiniIndex = None minIndex = None while i < attributesSize: giniIndex = Cart.getGiniIndex(data,i) if minGiniIndex == None or giniIndex < minGiniIndex: minGiniIndex = giniIndex minIndex = i print("第" , i ,"列的属性",attributes[i],"的基尼指数为:" , giniIndex) i += 1 print("第" , minIndex ,"列的属性",attributes[minIndex],"的基尼指数最小为:" , minGiniIndex ,";为最优划分属性") return minIndex # 获取基尼指数 data的最后一列认为是类型 @staticmethod def getGiniIndex(data,attributesIndex): # 首先按照属性下标(attributesIndex)拆分出多个子集, V = Cart.splitDataByIndex(data,attributesIndex) # 总数据大小 dSize = len(data) # 计算每个子集的Gini值,加权求和 rs = 0 for Dv in V.values(): dvSize = len(Dv) dvGini = Cart.getGini(Cart.getKMap(Dv),dvSize) rs += (dvSize/dSize) * dvGini return rs #按照属性下标(attributesIndex)拆分出多个子集,子集的集合为:V,每个子集为Dv @staticmethod def splitDataByIndex(data,attributesIndex): V = dict() for dLine in data: attribute = dLine[attributesIndex] Dv = V.get(attribute) if Dv is None: Dv = list() V[attribute] = Dv Dv.append(dLine) return V # 获取基尼值 @staticmethod def getGini(kMap,dSize): rs = 0 for item in kMap.values(): pk = (item/dSize) rs += pk * pk return 1 - rs @staticmethod def getMoreType(data): kMap = Cart.getKMap(data) maxCount = -1 maxName = None for key in kMap.keys(): if kMap.get(key) > maxCount: maxCount = kMap.get(key) maxName = key return maxName # 获取指定集合种类型->数量的映射 @staticmethod def getKMap(data): kMap = dict() for dLine in data: # 获取分类值k k = dLine[len(dLine) - 1] # 获取当前k出现的次数 kNum = kMap.get(k) if kNum is None: kMap[k] = 1 else: kMap[k] = kNum + 1 return kMap 节点类 class Node: name = "未命名节点" # 线描述,没有的是根节点 desc = "" # 子节点,长度为0的是叶节点 children = [] def __init__(self): self.children = [] def addChild(self, node): self.children.append(node) 画树类 class Tree: root = None # 定义决策节点以及叶子节点属性:boxstyle表示文本框类型,sawtooth:锯齿形;circle圆圈,fc表示边框线粗细 decisionNode = dict(boxstyle="round4", fc="0.5") leafNode = dict(boxstyle="circle", fc="0.5") # 定义箭头属性 arrow_args = dict(arrowstyle="<-") # 步长,每个节点的横线和纵向距离 step = 3 # 当前深度 deep = 0 # 当前深度的个数 nowDeepIndex = 0 # 当前深度和这个深度的当前节点数量的映射 deepIndex = dict() def __init__(self, root): self.root = root # 设定坐标范围 plt.xlim(0, 20) plt.ylim(-18, 0) # 设定中文支持 plt.rcParams["font.sans-serif"] = ["SimHei"] plt.rcParams["axes.unicode_minus"] = False # 绘制叶节点 # x1,y1 箭头起始点坐标 # x2,y2 箭头目标点(文字点坐标) # text 节点文字 # desc 线文字 def drawLeaf(self, x1, y1, x2, y2, text, desc): # 绘制节点以及箭头 plt.annotate(text, xy=(x1, y1), xytext=(x2, y2), va='center', ha='center', xycoords="data", textcoords='data', bbox=self.leafNode, arrowprops=self.arrow_args) # 绘制线上的文字 plt.text((x1 + x2) / 2, (y1 + y2) / 2, desc) # 绘制决策节点 def drawDecision(self, x1, y1, x2, y2, text, desc): # 绘制节点以及箭头 plt.annotate(text, xy=(x1, y1), xytext=(x2, y2), va='center', ha='center', xycoords="data", textcoords='data', bbox=self.decisionNode, arrowprops=self.arrow_args) # 绘制线上的文字 plt.text((x1 + x2) / 2, (y1 + y2) / 2, desc) # 绘制根节点(特殊决策节点) def drawRoot(self, text): # 绘制节点以及箭头 plt.annotate(text, xy=(0, 0), va='center', ha='center', xycoords="data", textcoords='data', bbox=self.decisionNode) def drawTree(self): self.draw0(self.root, 0, 0) plt.show() # xy是父节点的坐标 def draw0(self, node, x, y): # 如果当前深度节点数量没有,则置为0 if(self.deepIndex.get(self.deep) is None): self.deepIndex[self.deep] = 0 # 注意因为是基于当前节点数量排列所有节点,故都基于0点排列 x2 = self.deepIndex[self.deep] * self.step y2 = y - self.step if len(node.children) > 0: if len(node.desc) > 0: self.drawDecision(x, y, x2, y2, node.name, node.desc) self.deep += 1 for i, child in enumerate(node.children): self.draw0(child, x2, y2) self.deep -= 1 else: self.drawRoot(node.name) for i, child in enumerate(node.children): self.draw0(child, 0, 0) else: self.drawLeaf(x, y, x2, y2, node.name, node.desc) # 当前深度节点数++ self.deepIndex[self.deep] = self.deepIndex[self.deep] + 1 # 程序入口 cart = Cart(D,A) cart.draw() 测试checkDA方法 # D2=[ # ['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'], # ['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'], # ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'], # ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否']] # AA2 = [{'根蒂':1},{'脐部':4}] # a = Cart.checkDA(D2,AA2) # a2 = Cart.checkDA(D,[]) # a3 = Cart.checkDA(D,Cart.getAttributesAndIndex(A)) # print(a,a2,a3) 运行结果:
5.总结
5.1算法比较
| 算法名称 | ID3 | C4.5 | CART |
| 特征选择 | 信息增益,选择信息增益最大的特征 | 信息增益率,选择信息增益最小的特征 | Gini指数,选择Gini指数小的特征 |
| 记录划分 | 多元划分 | 多元划分 | 仅二元划分 |
| 停止分裂条件 | 信息增益小于阈值 | 信息增益比小于阈值 | Gini指数小于阈值或者样本个数小于阈值 |
| 剪枝方法 | 不支持 | 悲观错误剪枝 | 令损失函数最小或者Gini指数度量损失 |
5.2优缺点
1、优点:
- 简单直观,在逻辑上比较容易解释;
- 基本不需要预处理,不需要归一化和处理缺失值;
- 既可以处理离散值也可以处理连续值;
- 可以处理多分类问题;
- 使用决策树预测的代价是 ,m是样本数;
- 对异常点的容错能力好,健壮性高。
2、缺点:
- 非常容易过拟合,导致泛化能力不强。可通过限制树的深度和设置结点最少样本数来改进;
- 会因为样本的一点改进,导致树的结构剧烈变动。可以通过集成学习方法来改进;
- 若某些特征的样本比例过大,生成的树容易偏向这些特征。可通过调节样本权重来改进;
- 寻找最优的决策树是一个NP难题,容易陷入局部最优。可通过集成学习方法改进;
- 很难学习比较复杂的关系(如异或)。可换用神经网络方法来学习
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/125322.html