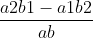矩阵和矢量的叉乘推导和简单实用

大家好，欢迎来到IT知识分享网。

手写了一份叉乘的推导

矩阵的叉乘

叉乘的矩阵形式，a向量变成A*  然后乘b向量

二维矩阵

假设a（a1,a2） b（b1,b2） 

aXb = a1b2 – a2b1  几何意义就是 aXb是a b组成的平行四边形的面积

接下来来证明

S(a,b) = ab*Sin<a,b> = b X a = a2b1 – a1b2

Sin<a,b> = Sin(α – β) = SinαCosβ – CosαSinβ = * – * =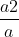 

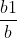
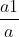
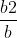
==>>   S(a,b) = a1b2 – a2b1

==>>   S(a,b) = 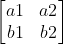 = a1b2 – a2b1

这两个值是相反的， S(a,b) = b X a 

因为 Sin<a,b> = Sin(α – β)   Sin<b,a> = Sin(β – α)    同时也跟矩阵aXb  bXa的右手坐标系有关

三维矩阵

  = a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31

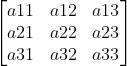
跟上面二阶行列式一样，都是正向对角相乘后的和 减去 反向对角相乘后的和

S(a,b,c) = a X b X c

这就可以来推测Unity里面Vector3的Cross 

 public static Vector3 Cross(Vector3 lhs, Vector3 rhs) { return new Vector3((float) ((double) lhs.y * (double) rhs.z - (double) lhs.z * (double) rhs.y), (float) ((double) lhs.z * (double) rhs.x - (double) lhs.x * (double) rhs.z), (float) ((double) lhs.x * (double) rhs.y - (double) lhs.y * (double) rhs.x)); }

这就是两个矢量的叉乘

所以求向量的叉乘可以转换为求对应矩阵的行列式

应用

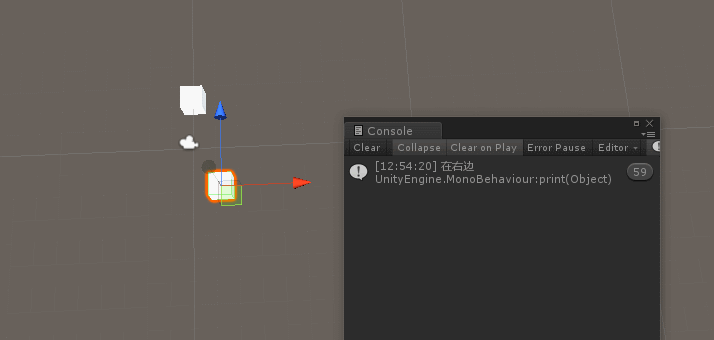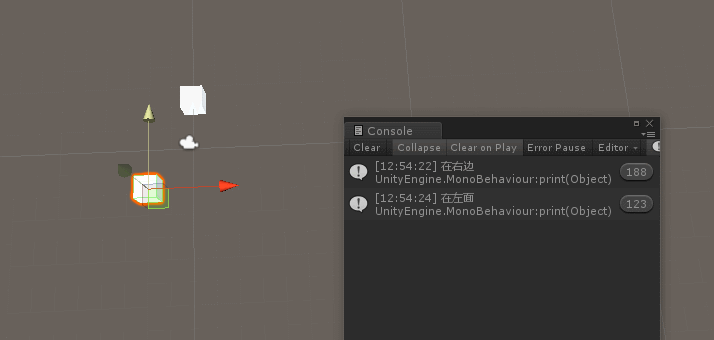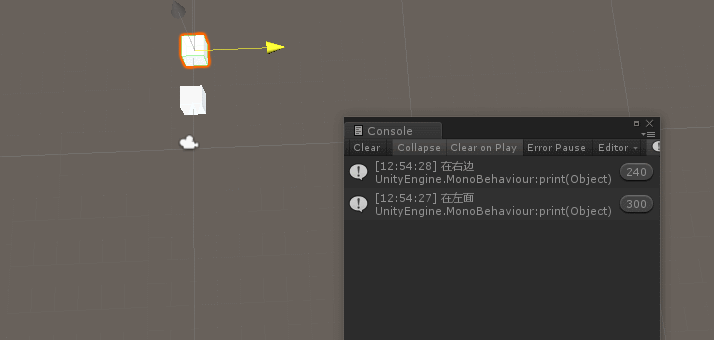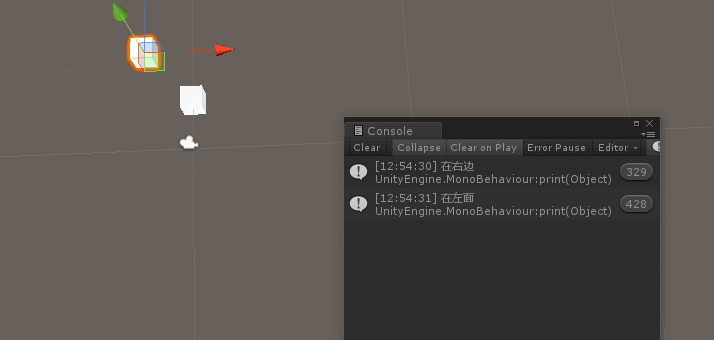
左手定则根据叉乘的正负判断 目标在主角的左面还是右面

 public Transform target; public Vector3 temp; void Start () { } void Update () { temp = Vector3.Cross(transform.position,target.position); if (temp.y > 0) { print("在左面"); } else { print("在右边"); } }

欢迎star我的框架 wang-er-s/Framework: a unity mvvm framework, building… (github.com)