R中的假设检验（二）方差分析

大家好，欢迎来到IT知识分享网。

Tukey代码例子：
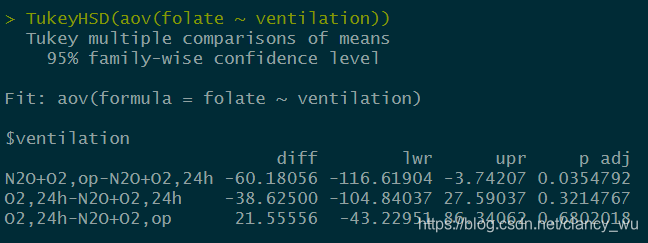
>TukeyHSD(aov(folate ~ ventilation)) #TukeyHSD是R自带的方法

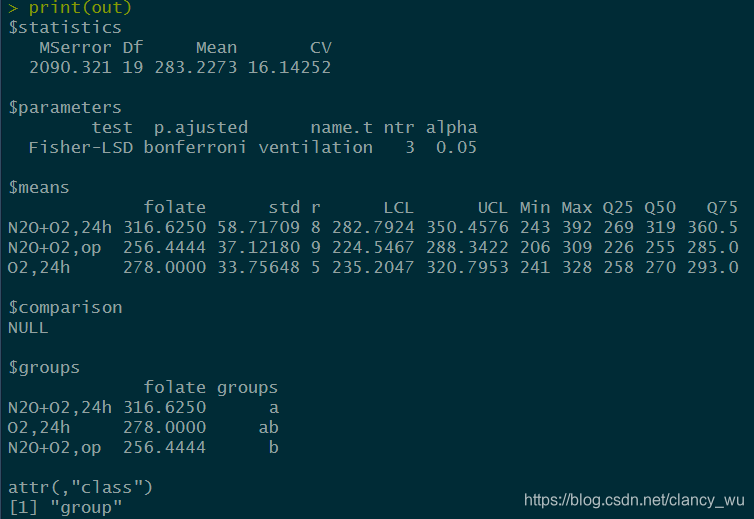
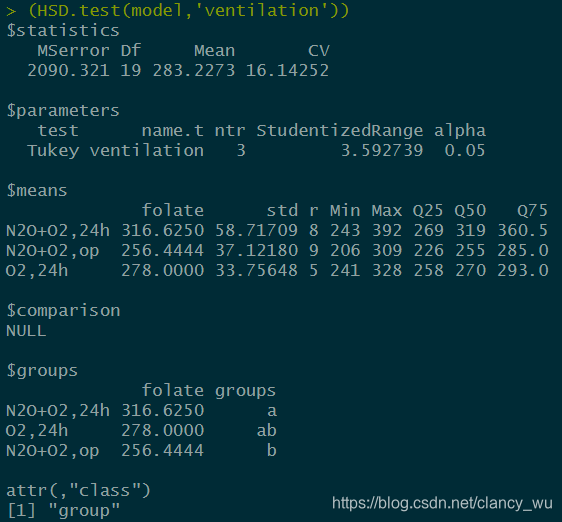
>HSD.test(aov(folate ~ ventilation),‘ventilation’) #这是agricolae包的HSD.test函数，听说是比TukeyHSD函数更好，我还没弄懂agricolae包的显示特点，等我以后弄懂了我再来回答，我先贴图供大家分析。

SNK代码例子：
>SNK.test(aov(folate ~ ventilation),‘ventilation’) #这是agricolae包的SNK.test函数
Scheffe代码例子：
>scheffe.test(aov(folate ~ ventilation),‘ventilation’) #这是agricolae包的scheffe.test函数
以上是最常见的几种方法。
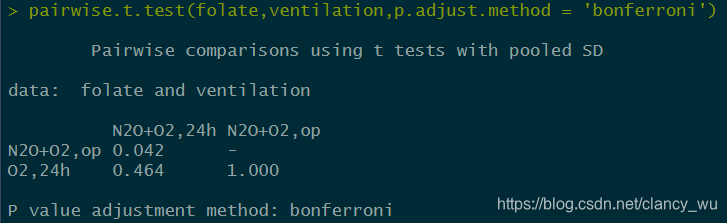
这里还有一种方法叫成对比较，pairwise.t.test，非常好用，，能显示成对比较的p值表。
代码示例 >pairwise.t.test(folate,ventilation,p.adjust.method = ‘bonferroni’)
注意这里的p.adjust.method，包括了c(“holm”, “hochberg”, “hommel”, “bonferroni”, “BH”, “BY”, “fdr”, “none”)。这个是R自带的两组比较的检验方法，输出的是各组两两比较的p值。如果p大于1，则输出1，这个p值的最大就是1。
平常建议使用这个，或者LSD，都可以。

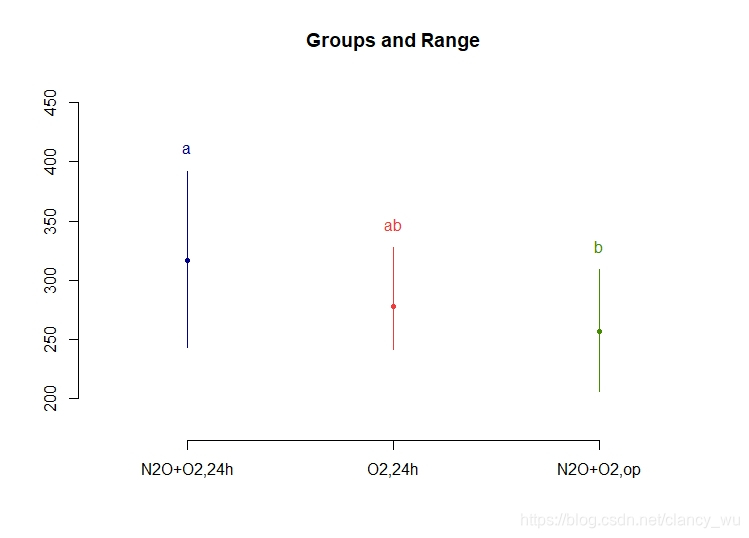
把这幅图和上面LSD的图比较可以发现，LSD用的是字母表示法，告诉你哪两组有差异，而pairwise.t.test是输出p值。但两者最后呈现的结果是一样的，因此根据需要选择。这个pairwise不用加载agricolae包，可能我比较喜欢，方便快捷。
保守的单因素方差分析
回顾前面，前面说了这么多，其实只是讲了ANOVA的分析，还记得么，它的前提条件是各组数据符合正态分布和方差齐，而这里要介绍Welch的方法，即只需要正态分布，不需要方差齐的检验方法，类似于t检验里，我们介绍过1次。话说Welth真是个保守的人呢，但是他的结果我感觉灵敏度比不上ANOVA。
代码例子：> oneway.test(folate ~ ventilation) #p=0.09277
可以看到，这里输出的p比上面ANOVA输出的p要大很多，结果也从显著的临界值变得不显著。这是个非常悲伤的故事，对于国内追求p值的研究者来说，这无异于是晴天霹雳，所以Welch虽然方便，但还是慎用。这零点几的正负就决定着文章能不能见刊了，说起来真是心酸。

非参数方差分析：Kruskal-Wallis检验
KW法，不假设各组的数据分布，仅假设各组具有相似的分布，适用于不符合正态分布的情况，比如偏峰分布。该方法比较简单，原假设同ANOVA。
代码例子： >kruskal.test(folate ~ ventilation) #p=0.1234
这没什么好说的，后面继续上面的多重检验环节。

以上即是常用的单因素方差分析，双因素方差分析例如anova( lm( hr ~ subj+time ) )，以及双因素非参数方差分析的Friedman检验例如friedman.test ( hr ~ time | subj )就不提了。这些我的领域用的太少太少了，所以我就随便过一遍，没有心思去了解。

重新审视线性回归和方差分析
我们说，anova（）函数是输出方差分析表，且这个模型的x需要是分类变量。但是，若x是离散变量呢？
当x是离散变量，x与y构建的一元线性回归模型，这个模型在前面讲过，这个模型的斜率是b，截距是a，而若把b定义为模型方差，把a定义为残差方差，那么对于同样构建成这个模型的方差分析，斜率是组间波动，截距是组内波动。所以，对b进行的统计检验其实就是对组间方差进行分析。
由此，可以运用F检验，对一元线性回归模型进行显著性检验，代入一元线性回归分析，即F检验是对原假设“回归模型的斜率为0”作出显著性检验。

今天我又回来了，重磅中的重磅，我来解释上面的两两比较中遗留的问题。这个原来是统计学的基础，但是因为我没看统计学原理书，所以这个基础知识点不知道。今天终于明白了。这个就是“多重比较的字母标记法”
多重比较的字母标记法：步骤：（1）将全部平均数从大到小顺序排列，然后在最大的平均数上标上字母a（2）将该平均数依次和其以下各水平均数相比，凡差异不显著的都标字母a，直至某一个与之相差显著的平均数则标以字母b（3）再以该表有b的平均数为标准，与上方各个比它大的平均数比，凡不显著的也一律表以字母b（4）重复以上步骤，标c，d…（5）这样各平均数间，凡有一个标记相等字母的即为差异不显著，凡具有不同标记字母的即为差异显著。在实际应用时，一般以大写字母A,B,C…表示α=0.01显著水平，以小写字母a，b，c…表示α=0.05显著水平。

如此一来，上面的所有的两两比较的方法都通悟了，今天的收获非常的大。这个坑填上了。