【MATLAB图像处理】图像复原

大家好，欢迎来到IT知识分享网。

理论：

图像复原：图像复原是图像处理的主要内容之一，所谓图像复原就是指去除或减轻在图像获取过程中发生的图像质量的下降。成像过程中的图像“退化”，是指由于成像系统各种因素的影响，使得图像质量降低。图像复原可以看成图像退化的逆过程，是将图像退化的过程加以估计，建立退化的数学模型后，补偿退化过程造成的失真。与图像增强相似，图像复原的目的也是改善图像质量。图像增强主要是一个主观过程，而图像复原主要是一个客观过程。图像增强被认为是一种对比度拉伸，提供给用户喜欢接收的图像：而图像复原技术追求恢复原始图像的最优估值。

图像退化： 图像的质量变坏叫做退化。退化的形式有图像模糊、图像有干扰等。

       图像复原是在研究图像退化原因的基础上，以退化图像为依据，根据一定的先验知识，建立一个退化模型，然后用相反的运算，以恢复原始景物图像。如果我们对退化的类型、机制和过程都十分清楚，那么就可以利用其反过程把己退化的图像复原。图像复原主要取决于对图像退化过程的先验知识掌握的精确程度。图像复原要明确规定质量准则，即衡量接近 原始景物图像的程度，如：最小均方误差准则、加权均方准则、最大熵准则等。图像复原模型可以用连续数学或离散数学处理。典型的图像复原是根据图像退化的先验知识建立一个退化模型，以此模型为基础，采用各种反退化方法，例如滤波等，使复原后的图像符合某些准则，图像质量得到改善。

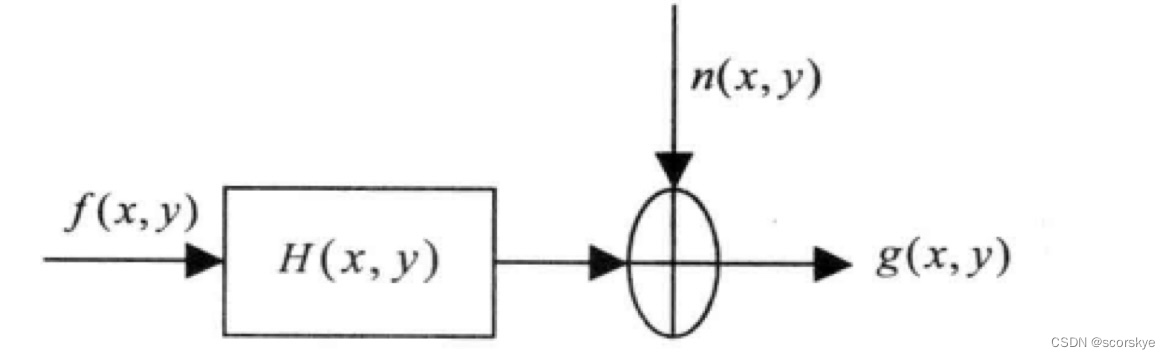
连续图像退化的数学模型：

 输入图像f(x,y)经过一个退化系统或退化算子H(x,y)后产生的退化图像g(x,y)可以表示为：

g(x,y)=H[f(x,y)]

如果仅考虑加性噪声的影响，则退化图像可表示为：

g(x,y)=H[f(x,y)]+n(x,y)

H(x,y)是h(x,y)的傅里叶变化，h(x,y)成为退化系统的冲激响应函数。在图像形成的光学系统中，冲击为一光点。因而又将h(x,y)称为退化系统的点扩展函数PSF（Point Spread Function）。此时，退化系统的输出就是输入图像f(x,y)与点扩展函数h(x,y)的卷积。

卷积操作就是将卷积核取输入图像的每一个像素点作为中心像素，将中心像素和周围像素与卷积核对应位置的权重相乘并加和，得到的值作为输出图像对应中心像素位置的像素值。

实验：

1.观察均值模糊与运动模糊

图1 均值模糊与两组不同参数的运动模糊

        观察图一可以发现：两种噪声模糊的形式是不同的，因为均值模糊（Disk Bluer）是将单个像素与周围像素作平均处理得到像素值形成新的矩阵作为输出模糊图像，参数为模糊核的大小；而运动模糊（Motion Blur）是一种通常由于相机或被拍摄物体的运动引起的模糊，运动长度（参数一）表示运动的距离，通常用像素或毫米来表示，运动角度（参数二）表示运动方向相对于图像的水平方向的偏角。

        当均值模糊的模糊核增大，模糊程度增强；当运动模糊的运动长度增大/减小，像素运动的距离也就增大/减小，当运动角度增大/减小，运动方向相对于图像的水平方向的偏角就逆时针增大/减小。

% 运动PSF均值PSF I=rgb2gray(imread('exp2.jpg')); subplot(2,2,1); imshow(I); title('Original Image'); % 创建运动PSF并进行图像模糊 len = 21; % 运动模糊长度 theta = 11; % 运动方向 len2 = 51; theta2 = 90; psf = fspecial('motion', len, theta); blurred_img = imfilter(I, psf, 'conv', 'circular'); subplot(2,2,3); imshow(blurred_img); title('Motion Blur（21-11）'); psf2 = fspecial('motion', len2, theta2); blurred_img2 = imfilter(I, psf2, 'conv', 'circular'); subplot(2,2,4); imshow(blurred_img2); title('Motion Blur（51-90）'); % 创建均值PSF并进行图像模糊 psf = fspecial('disk', 5); % 均值模糊核大小为5^2*pi blurred_img = imfilter(I, psf ,'conv', 'circular'); subplot(2,2,2); imshow(blurred_img); title('Disk Blur');

‘conv’表示卷积操作， ‘circular’表示循环赋值，防止卷积核在滑动到图像尺寸边缘时自动填充零值，造成结果的边缘效应和锯齿结构。

2.观察不同的噪声

图2 添加加性高斯噪声和椒盐噪声 

        观察图二可以发现：加性高斯噪声图像是由生成与原图同样大小的呈高斯分布的控制强度的矩阵加在原图上形成的噪声图像，此噪声图像上分布白点。椒盐噪声是在原图上随机位置的像素取其为最大值（1）或最小值（0）形成的噪声图像，此噪声图像上分布着随机的黑白点。

I=rgb2gray(imread('exp2.jpg')); subplot(1,3,1); imshow(I); title('Original Image'); %添加加性高斯噪声噪声 noise=0.1*randn(size(I)); im_noise1=imadd(I,im2uint8(noise)); subplot(1,3,2); imshow(im_noise1); title('Multiplicative noise'); %添加椒盐噪声 im_noise2 = imnoise(I, 'salt & pepper'); subplot(1,3,3); imshow(im_noise2); title('Salt & Pepper noise');

3.观察模糊图像的真实与非真实的复原

图3 对模糊图像进行真实与非真实滤波

        观察图三可以发现：当我们知道图像是如何损坏的的或着说退化的，也就是知道了先验知识，即点扩散函数PSF已知，在使用维纳滤波时带入PSF作为参数，就可以完成真实滤波，所得到的复原图像就十分接近原图像；当我们不知道先验知识，即点扩散函数PSF未知，在使用维纳滤波时用的数学模型是估计值，如此操作就是非真实滤波，所得到的复原图像与原图差别很大。

% 运动PSF无噪声真实+非真实复原 I=rgb2gray(imread('exp2.jpg')); subplot(2,3,1); imshow(I); title('Original Image'); % 创建运动PSF并进行图像模糊 len = 21; % 运动长度 theta = 11; % 运动方向 psf = fspecial('motion', len, theta); blurred_img = imfilter(I, psf, 'conv','circular'); subplot(2,3,3); imshow(blurred_img); title('Motion Blur(21-11)'); wnr=deconvwnr(blurred_img,psf); subplot(2,3,4); imshow(wnr); title('Restored Image (RWiener)');%真实图像复原 psf2 = fspecial('motion', 2*len, theta); psf3 = fspecial('motion', len, 2*theta); wnr1=deconvwnr(blurred_img,psf2); wnr2=deconvwnr(blurred_img,psf3); subplot(2,3,5); imshow(wnr1); title('Restored Image (2*len Non-Uniform Wiener Filtering)');%非真实图像复原 subplot(2,3,6); imshow(wnr2); title('Restored Image (2*theta Non-Uniform Wiener Filtering)');%非真实图像复原

4.观察噪声模糊图像的含信噪比和自相关函数的复原

图4 对噪声加模糊图像进行含信噪比和自相关函数滤波

        观察图4可以发现：对含噪声的模糊图像仅利用PSF作为参数进行维纳滤波，得到的图像与原图差别很大，是看似无规则的黑白点；而加入信噪比作为增加的参数进行维纳滤波，得到的图像与原图像近似；再增加噪声自相关函数与图像自相关函数两个参数进行维纳滤波，得到的图像也与原图像近似，效果与加入信噪比参数类似。

        由此可以得到，当进行维纳滤波图像复原时，所提供的维纳滤波参数越多，图像复原的效果越好。

% 运动PSF有噪声直接滤波+信噪比+自相关函数滤波 I=rgb2gray(imread('exp2.jpg')); subplot(2,3,1); imshow(I); title('Original Image'); % 创建运动PSF并进行图像模糊 len = 21; % 运动长度 theta = 11; % 运动方向 psf = fspecial('motion', len, theta); blurred_img = imfilter(I, psf, 'conv', 'circular'); noise=0.1*randn(size(I)); BlurredNoisy=imadd(blurred_img,im2uint8(noise)); subplot(2,3,3); imshow(BlurredNoisy); title('Motion Blur & Noisy'); wnr1=deconvwnr(BlurredNoisy,psf); subplot(2,3,4); imshow(wnr1); title('Noisy Restored Image (RWiener)'); NSR=sum(noise(:).^2)/sum(im2double(I(:)).^2); %计算信噪比 wnr2=deconvwnr(BlurredNoisy,psf,NSR); subplot(2,3,5); imshow(wnr2); title('Noisy Restored Image (RWiener with NSR)'); NP=abs(fftn(noise)).^2; %噪声能量谱密度 NCORR=fftshift(real(ifftn(NP))); %噪声自相关函数 IP=abs(fftn(im2double(I))).^2; %图像能量谱密度 ICORR=fftshift(real(ifftn(IP))); %图像自相关函数 wnr3=deconvwnr(BlurredNoisy,psf,NCORR,ICORR); subplot(2,3,6); imshow(wnr3); title('Noisy Restored Image (RWiener with AF)');

思考：

• 不同的 PSF 对复原效果有什么影响？

PSF是点扩散函数，用于描述传递过程中的模糊过程，不同的PSF可以描述不同类型的模糊，例如运动模糊、均值模糊等。不同的PSF会对复原效果产生不同的影响：

1. PSF尺寸：PSF的尺寸越大，图像就会被更强烈地模糊，因此在复原时，需要用更大的卷积核来提取图像的信息，从而得到更好的复原效果。
2. PSF形状：PSF的形状影响图像的复原效果。例如，对于运动模糊，其PSF通常是线性的，复原时需要使用逆滤波或者最小二乘法等方法；对于径向模糊，其PSF通常是环形的，复原时需要使用维纳滤波等方法。
3. PSF噪声：PSF噪声也会影响复原效果。如果PSF噪声较大，则需要使用逆滤波等方法来降低其影响。
4. PSF变化：如果PSF是随机变化的，复原就会变得更加困难。为了解决这个问题，可以使用一些先进的复原算法，例如基于深度学习的方法等。