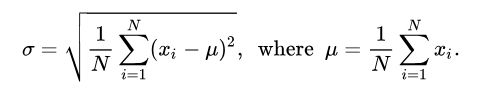统计学常用指标

大家好，欢迎来到IT知识分享网。

标准差(SD)

标准差（StandardDeviation），在概率统计中最常使用作为统计分布程度（statisticaldispersion）上的测量。标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。它反映组内个体间的离散程度。一个较低的标准差表示这些值趋向于接近平均(也称为期望值)的集合，而较高的标准差表示这些值分布在更大的范围内。标准差的平方即方差。

自变量,x, 总数,n
因变量,y
预测值,f 下同

f = w*x +b SD = math.sqrt( sum(np.square(f - np.mean(f))) / n ) 

均方根误差(RMSE/RMSD)

RMSE = math.sqrt( sum(np.square(f - y) ) / n ) 

均方误差(MSE/MSD)

Mean Square Error，均方误差。均方根误差的平方。通过平方的形式便于求导，所以常被用作线性回归的损失函数。

MSE = sum(np.square(f - y) ) / n 

平均绝对误差(MAE)

MAE = sum(np.abs(f - y) ) / n 

决定系数/拟合优度(R^2)

Residual = sum( np.square(y - f) ) # 残差平方和 total = sum( np.square( y - np.mean(y) ) ) #总体平方和 R_square = 1 - Residual / total # 相关性系数R^2 

平均偏差(Bias)

sum(f - y) / n