【数据结构】哈夫曼树

大家好，欢迎来到IT知识分享网。

【数据结构】哈夫曼树

1.什么是哈夫曼树

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近

2.哈夫曼树的基本概念

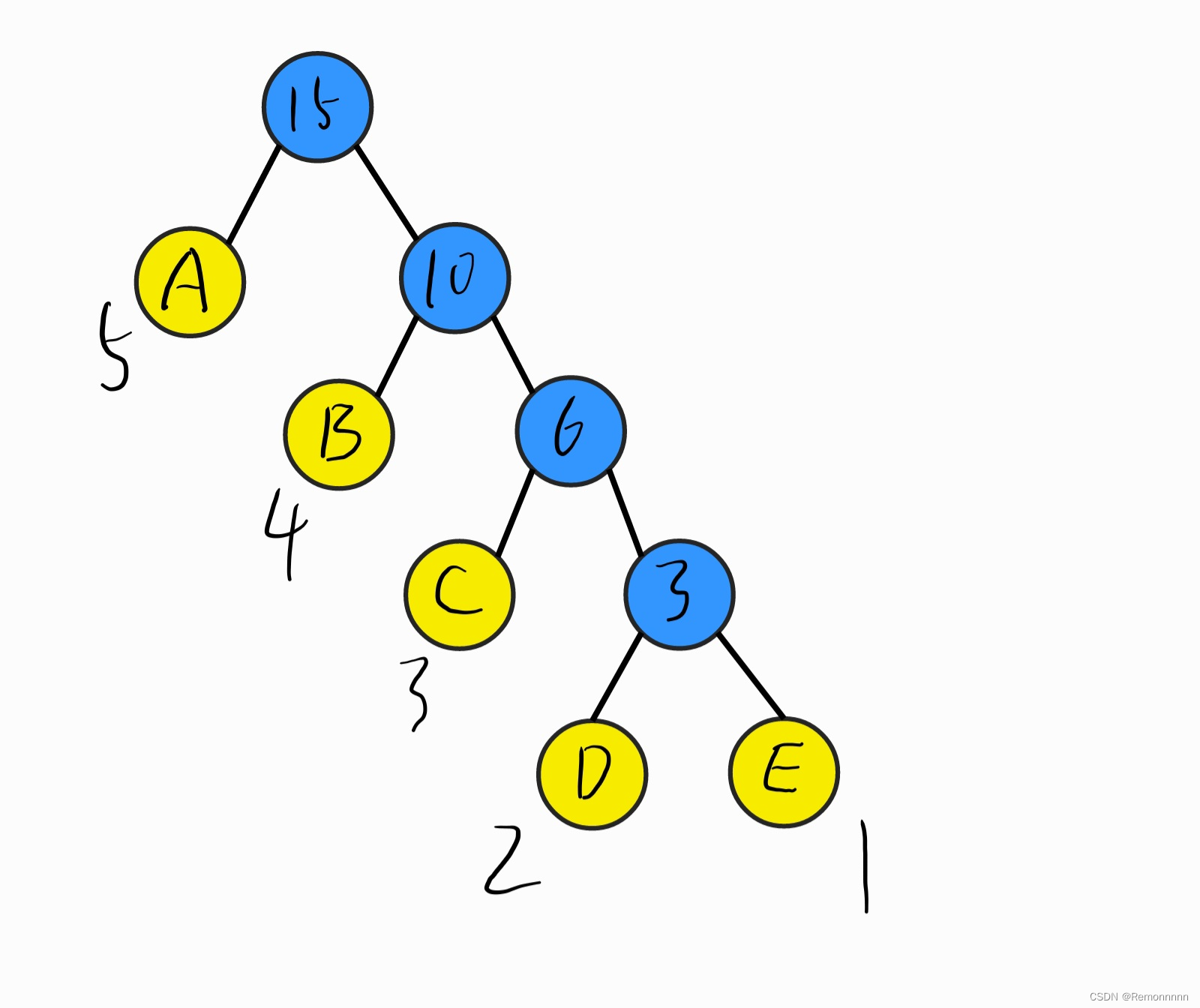
路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。（如15->A的路径长度就为1）

结点的路径长度：两结点间路径上的分支数

树的路径长度（TL）：从树的根结点到每一个节点的路径长度之和（TL=0+1+1+2+2+3+3+4+4=20）

权：赋给树中结点的一个特殊值，根据不同场合有不同的意义

结点的带权路径长度：从根结点到该结点的路径长度乘结点上的权

树的带权路径长度：所有叶子结点的带权路径长度之和（WPL=5×1+4×2+3×3+2×4+1×4=34）

最优树(哈夫曼树)：带权路径长度最短的树

3.哈夫曼树的构建

一个结点的构建

struct Node { 
    char val;//存储的字符 int weight;//权值 Node* left; Node* right; }; 

哈夫曼树的创建

struct cmp//比较函数 { 
    bool operator()(Node* a, Node* b) { 
    return a->weight > b->weight;//自定义比较规则 } }; priority_queue<Node*,vector<Node*>,cmp>que;//采用小根堆的优先队列存储结点，保证权值小的结点先被构建 Node* Create_HaffmanTree(vector<int>nums, string str) { 
    for (int i = 0; i < nums.size(); i++) { 
    Node* newnode = new Node; newnode->weight = nums[i]; newnode->val = str[i]; newnode->left = NULL; newnode->right = NULL; que.push(newnode); } while (que.size() > 1)//直到队列只剩一个结点 { 
    Node* newnode = new Node;//构建新的结点， newnode->val = '#';//创建的结点val用'#'表示 newnode->left = que.top(); newnode->weight = que.top()->weight; que.pop(); newnode->right = que.top(); newnode->weight += que.top()->weight; que.pop(); que.push(newnode);//将创建好的新结点入队 } return que.top();//返回根结点 } 

4.哈夫曼编码

基本概念：在远程通讯中,要将待传字符转换成由二进制的字符串

但这种构建有重码的风险，因此哈夫曼编码的关键在于要设计长度不等的编码,任一字符的编码不能是另一个字符的编码的前缀，这种编码也叫前缀编码，让出现次数多的字符尽量采取短的编码

因此，我们可以利用哈夫曼树的特点，权值越大的结点离根结点越近，路径越短，并将结点的左分支标记为0，右分支标记为1

哈夫曼编码

string HaffmanCode(Node* root, char s, string code)//这里采取dfs遍历 { 
    if (root->left == NULL && root->right == NULL)//当遍历到叶子结点时，判断是否为要找的字符 { 
    if (root->val == s) { 
    return code;//找到则返回该code } else { 
    return "-1";//不是则返回'-1' } } if (root->left != NULL) { 
    string tmp = HaffmanCode(root->left, s, code + '0'); if (tmp != "-1") { 
    return tmp; } } if (root->right != NULL) { 
    string tmp = HaffmanCode(root->right, s, code + '1'); if (tmp != "-1") { 
    return tmp; } } return "-1"; } string Create_HaffmanCode(Node* root, string str)//str为传入需要编码的字符串 { 
    string code; for (int i = 0; i < str.size(); i++) { 
    code += HaffmanCode(root, str[i], ""); } return code; } 

同理，翻译时也按照该规则遍历

哈夫曼编码的翻译

string Translate_HaffmanCode(Node* root, string code) { 
    string str; for (int i=0;i<code.size();) { 
    Node* rear = root; while (rear->left != NULL && rear->right != NULL && i<code.size())//遍历到叶子结点时跳出 { 
    if (code[i] == '0')//code只有可能为0或1的一种（这里不考虑无法翻译的编码） { 
    rear = rear->left; } else { 
    rear = rear->right; } i++; } str += rear->val; } return str; } 

完整代码

#include<bits/stdc++.h> using namespace std; struct Node { 
    char val; int weight; Node* left; Node* right; }; struct cmp { 
    bool operator()(Node* a, Node* b) { 
    return a->weight > b->weight; } }; priority_queue<Node*, vector<Node*>, cmp>que; Node* Create_HaffmanTree(vector<int>nums, string str) { 
    for (int i = 0; i < nums.size(); i++) { 
    Node* newnode = new Node; newnode->weight = nums[i]; newnode->val = str[i]; newnode->left = NULL; newnode->right = NULL; que.push(newnode); } while (que.size() > 1) { 
    Node* newnode = new Node; newnode->val = '#'; newnode->left = que.top(); newnode->weight = que.top()->weight; que.pop(); newnode->right = que.top(); newnode->weight += que.top()->weight; que.pop(); que.push(newnode); } return que.top(); } string HaffmanCode(Node* root, char s, string code) { 
    if (root->left == NULL && root->right == NULL) { 
    if (root->val == s) { 
    return code; } else { 
    return "-1"; } } if (root->left != NULL) { 
    string tmp = HaffmanCode(root->left, s, code + '0'); if (tmp != "-1") { 
    return tmp; } } if (root->right != NULL) { 
    string tmp = HaffmanCode(root->right, s, code + '1'); if (tmp != "-1") { 
    return tmp; } } return "-1"; } string Create_HaffmanCode(Node* root, string str) { 
    string code; for (int i = 0; i < str.size(); i++) { 
    code += HaffmanCode(root, str[i], ""); } return code; } string Translate_HaffmanCode(Node* root, string code) { 
    string str; for (int i=0;i<code.size();) { 
    Node* rear = root; while (rear->left != NULL && rear->right != NULL && i<code.size()) { 
    if (code[i] == '0') { 
    rear = rear->left; } else { 
    rear = rear->right; } i++; } str += rear->val; } return str; } int main() { 
    string str = "ABCDE"; vector<int>nums = { 
    1,2,3,4,5 }; Node* root = Create_HaffmanTree(nums,str); string code = Create_HaffmanCode(root, str); cout << code << endl; cout << Translate_HaffmanCode(root, code); return 0; } 

测试数据：str=ABCDE，weigh（权）={1,2,3,4,5}