最小二乘法，加权最小二乘法，迭代重加权最小二乘法 (含代码)【最小二乘线性求解】

大家好，欢迎来到IT知识分享网。

原文链接：地址

这里推荐一个视频推导过程：利用矩阵求偏导得出 $x$=$(A^{T}A{)}^{-1}{A}^{T}B$矩阵乘法求导视频

一：最小二乘法（OLS）

1：概述

2：代数式

分别对$a_0和a_1$求偏导，这里$a_0和a_1$就是未知参数

3：矩阵式（推荐）

举例：曲线拟合中最基本和最常用的是直线拟合。设$x$和$y$之间的函数关系为：一元一次函数$y＝f(a_0,a_1)＝a_0+a_{1}x$ 使用矩阵表达：$Ax=B$， 求$x$向量参数

推导过程我会在最后放上链接。那么：

一元多项式矩阵表达和一元一次项矩阵表达是一样的：$Ax=B$

3.1：实现代码

/* 普通最小二乘 Ax = B * (A^T * A) * x = A^T * B * x = (A^T * A)^-1 * A^T * B */ Array<double,Dynamic,1> GlobleFunction::leastSquares(Matrix<double,Dynamic,Dynamic> A, Matrix<double,Dynamic,1> B) { 
      //获取矩阵的行数和列数 int rows = A.rows(); int col = A.cols(); //A的转置矩阵 Matrix<double,Dynamic,Dynamic> AT; AT.resize(col,rows); //x矩阵 Array<double,Dynamic,1> x; x.resize(col,1); //转置 AT AT = A.transpose(); //x = (A^T * A)^-1 * A^T * B x = ((AT * A).inverse()) * (AT * B); return x; } 

Matrix是Eigen库中的一个矩阵类，这里引入Eigen库方便代数运算。

二：加权最小二乘法（WLS）

加权最小二乘法是对原模型进行加权，使之成为一个新的不存在异方差性的模型，然后采用普通最小二乘法估计其参数的一种数学优化技术。百度百科

1：增加对角矩阵 W

在最小二乘法的基础上增加一个对角矩阵$W$，对每组数据赋予不同的权重。

$W^T\ast W$对角矩阵每个数据的平方,消除负数。

1.1：实现代码

/* 加权最小二乘（WLS） W为对角线矩阵 * W²(Ax - B) = 0 * W²Ax = W²B * (A^T * W^T * W * A) * x = A^T * W^T * W * B * x = (A^T * W^T * W * A)^-1 * A^T * W^T * W * B */ Array<double,Dynamic,1> GlobleFunction::reweightedLeastSquares(Matrix<double,Dynamic,Dynamic> A, Matrix<double,Dynamic,1> B,Array<double,Dynamic,1> vectorW) { 
      //获取矩阵的行数和列数 int rows = A.rows(); int col = A.cols(); //vectorW为空,默认构建对角线矩阵1 if(vectorW.isZero()) { 
      vectorW.resize(rows,1); for(int i=0;i<rows;++i) { 
      vectorW(i,0) = 1; } } //A的转置矩阵 Matrix<double,Dynamic,Dynamic> AT; AT.resize(col,rows); //x矩阵 Array<double,Dynamic,1> x; x.resize(col,1); //W的转置矩阵 Matrix<double,Dynamic,Dynamic> WT,W; W.resize(rows,rows); WT.resize(rows,rows); //生成对角线矩阵 W = vectorW.matrix().asDiagonal(); //转置 WT = W.transpose(); //转置 AT AT = A.transpose(); // x = (A^T * W^T * W * A)^-1 * A^T * W^T * W * B x = ((AT * WT * W * A).inverse()) * (AT * WT * W * B); return x; } 

Matrix是Eigen库中的一个矩阵类，这里引入Eigen库方便代数运算。

三：迭代重加权最小二乘法（IRLS）

1：迭代重新加权最小二乘法（也叫迭代加权最小二乘法）( IRLS ) 的方法用于解决具有$p$范数形式的目标函数的某些优化问题：维基百科。迭代加权可以对目标函数和已知的数据来进行拟合，但是这时候有的数据对总体目标函数离得特别远，参与最小二乘法的时候就会对估计参数有很大的影响，这时候就要对参数进行优化，对数据较远的赋予较小的权重（不让它显得很重要，也就影响比较小），对数据较近的赋予较大的权重（影响大）。迭代加权最小二乘，是建立加权最小二乘上进行一个迭代来估值达到最优。

2：下面引入一片论文中的一段迭代方法求解 论文地址：Burrus, C.S. (2014). Iterative Reweighted Least Squares ∗.

MATLAB代码1：

% m-file IRLS0.m to find the optimal solution to Ax=b % minimizing the L_p norm ||Ax-b||_p, using basic IRLS. % csb 11/10/2012 function x = IRLS0(A,b,p,KK) if nargin < 4, KK=10; end; x = pinv(A)*b; % Initial L_2 solution E = []; for k = 1:KK % Iterate e = A*x - b; % Error vector w = abs(e).^((p-2)/2); % Error weights for IRLS W = diag(w/sum(w)); % Normalize weight matrix WA = W*A; % apply weights x = (WA'*WA)\(WA'*W)*b; % weighted L_2 sol. ee = norm(e,p); E = [E ee]; % Error at each iteration end plot(E) 

MATLAB代码2：

% m-file IRLS1.m to find the optimal solution to Ax=b % minimizing the L_p norm ||Ax-b||_p, using IRLS. % Newton iterative update of solution, x, for M > N. % For 2<p<infty, use homotopy parameter K = 1.01 to 2 % For 0<p<2, use K = approx 0.7 - 0.9 % csb 10/20/2012 function x = IRLS1(A,b,p,K,KK) if nargin < 5, KK=10; end; if nargin < 4, K = 1.5; end; if nargin < 3, p = 10; end; pk = 2; % Initial homotopy value x = pinv(A)*b; % Initial L_2 solution E = []; for k = 1:KK % Iterate if p >= 2, pk = min([p, K*pk]); % Homotopy change of p else pk = max([p, K*pk]); end e = A*x - b; % Error vector w = abs(e).^((pk-2)/2); % Error weights for IRLS W = diag(w/sum(w)); % Normalize weight matrix WA = W*A; % apply weights x1 = (WA'*WA)\(WA'*W)*b; % weighted L_2 sol. q = 1/(pk-1); % Newton's parameter if p > 2, x = q*x1 + (1-q)*x; nn=p; % partial update for p>2 else x = x1; nn=2; end % no partial update for p<2 ee = norm(e,nn); E = [E ee]; % Error at each iteration end plot(E) 

C++代码：

 /* 迭代重加权最小二乘（IRLS） W为权重,p为范数 * e = Ax - B * W = e^(p−2)/2 * W²(Ax - B) = 0 * W²Ax = W²B * (A^T * W^T * W * A) * x = A^T * W^T * W * B * x = (A^T * W^T * W * A)^-1 * A^T * W^T * W * B * 参考论文地址：https://www.semanticscholar.org/paper/Iterative-Reweighted-Least-Squares-%E2%88%97-Burrus/9b9218e7233f4d0b491e1582c893c9a099470a73 */ Array<double,Dynamic,1> GlobleFunction::iterativeReweightedLeastSquares(Matrix<double,Dynamic,Dynamic> A, Matrix<double,Dynamic,1> B,double p,int kk) { 
      /* x(k) = q x1(k) + (1-q)x(k-1) * q = 1 / (p-1) */ //获取矩阵的行数和列数 int rows = A.rows(); int col = A.cols(); double pk = 2;//初始同伦值 double K = 1.5; double epsilong = 10e-9; // ε double delta = 10e-15; // δ Array<double,Dynamic,1> x,_x,x1,e,w; x.resize(col,1); _x.resize(col,1); x1.resize(col,1); e.resize(rows,1); w.resize(rows,1); //初始x 对角矩阵w=1 x = reweightedLeastSquares(A,B); //迭代 最大迭代次数kk for(int i=0;i<kk;++i) { 
      //保留前一个x值,用作最后比较确定收敛 _x = x; if(p>=2) { 
      pk = qMin(p,K*pk); } else { 
      pk = qMax(p,K*pk); } //偏差 e = (A * x.matrix()) - B; //偏差的绝对值// 求矩阵绝对值 ：e = e.cwiseAbs(); 或 e.array().abs().matrix() e = e.abs(); //对每个偏差值小于delta,用delta赋值给它 for(int i=0;i<e.rows();++i) { 
      e(i,0) = qMax(delta,e(i,0)); } //对每个偏差值进行幂操作 w = e.pow(p/2.0-1); w = w / w.sum(); x1 = reweightedLeastSquares(A,B,w); double q = 1 / (pk-1); if(p>2) { 
      x = x1*q + x*(1-q); } else { 
      x = x1; } //达到精度,结束 if((x-_x).abs().sum()<epsilong) { 
      return x; } } return x; } 

C++实现代码和MATLAB基本一样，不过有稍微改进，其中参考了维基百科和Burrus, C.S. (2014). Iterative Reweighted Least Squares ∗.

四：应用

以下针对超定方程组来求解的。数据个数大于未知参数。

1:拟合圆（算法：迭代重新加权最小二乘）

2: 直线拟合（算法：迭代重新加权最小二乘）

1： $y=a_0+a_{1}x$
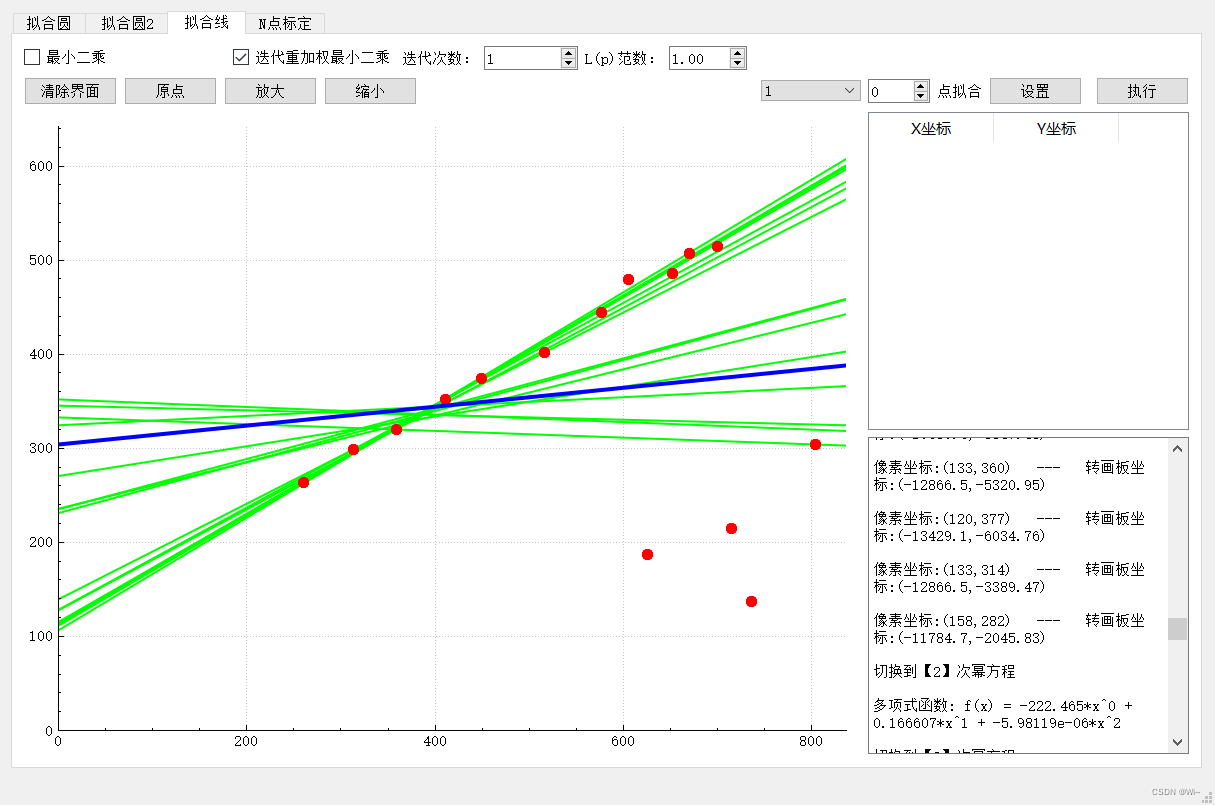
下面这张图使用的是最小二乘法，可以看出下面较远的数据噪点对整体密集数据有了很大的影响。
1.2：使用迭代重加权最小二乘
第1次迭代
…
第100次迭代
经过$n$次迭代后，噪点基本上对整体没有什么影响了，这时候的得到的参数也就是理想的。

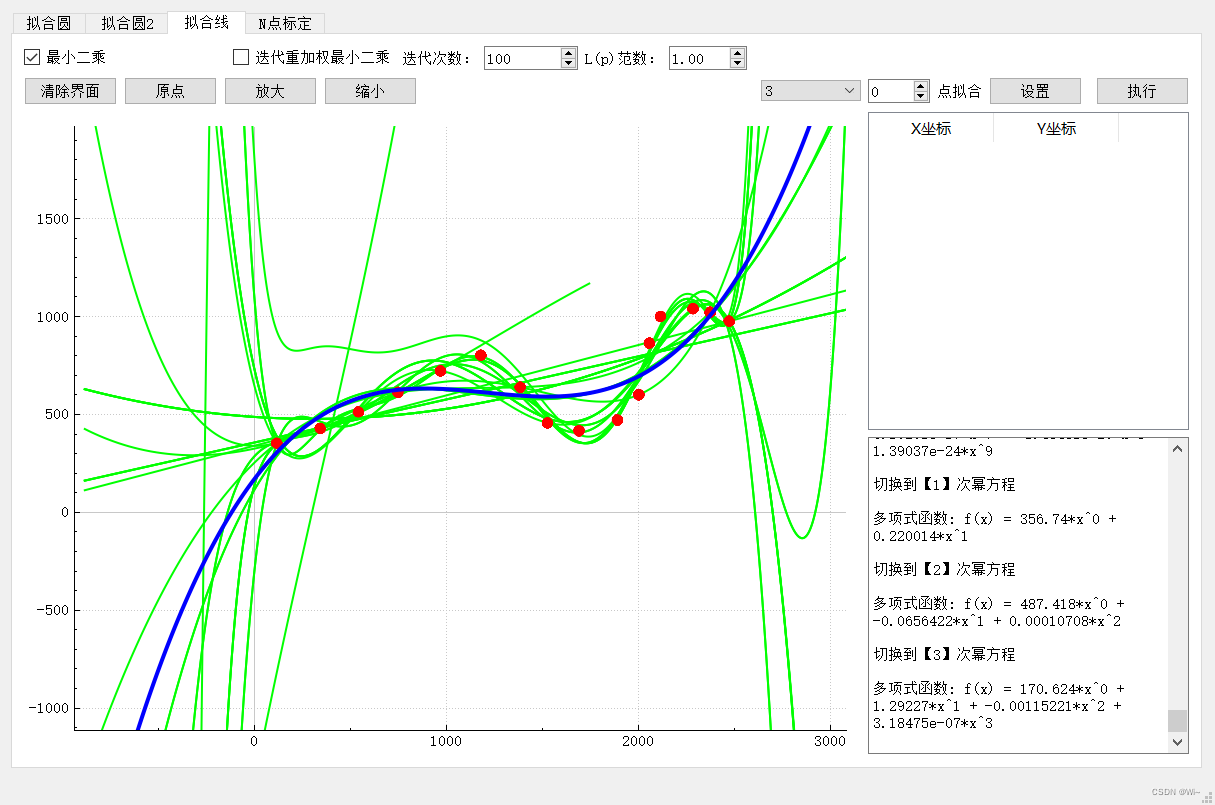
3:曲线拟合（算法：最小二乘）

一次函数拟合：

二次函数拟合：

三次函数拟合：

四次函数拟合：

五次函数拟合：

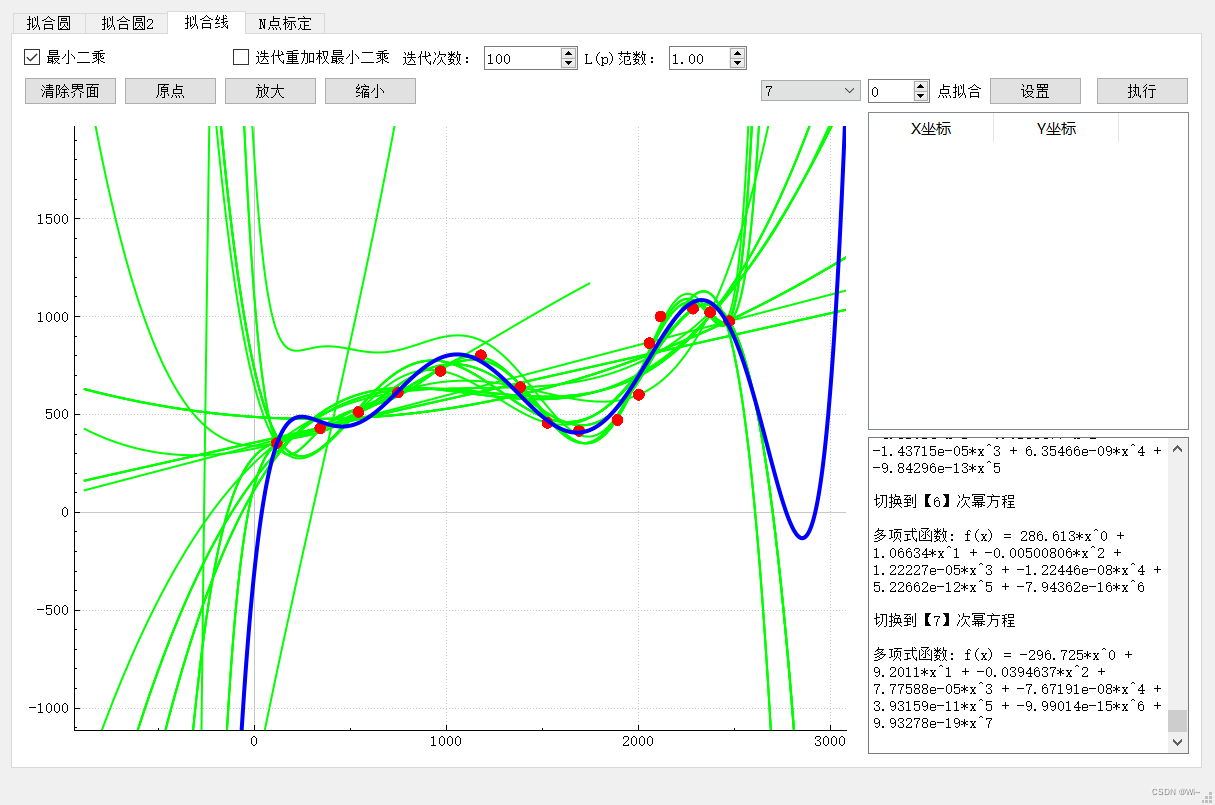
六次函数拟合：

七次函数拟合：

八次函数拟合：

4：N点标定（包括9点标定）（算法：最小二乘）

五：总结

2：上面完整代码已上传GitHub