统计学中的三大相关系数

大家好，欢迎来到IT知识分享网。

1. 皮尔森相关性系数【person】

上述公式中的分母是变量的标准差，这就意味着计算皮尔逊相关性系数时，变量的标准差不能为0（分母不能为0），也就是说你的两个变量中任何一个的值不能都是相同的。如果没有变化，用皮尔逊相关系数是没办法算出这个变量与另一个变量之间是不是有相关性的。

皮尔逊相关系数对数据的要求比较高：

1.实验数据通常假设是成对的来自正态分布的总体，因为我们在求皮尔逊相关性系数之后，还会用t检验等方法进行皮尔逊相关性系数检验，t检验是基于数据呈正态分布的。

2.皮尔逊相关性系数受异常值的影响比较大。

2.斯皮尔曼相关性系数【spearman】

斯皮尔曼相关性系数，通常也叫斯皮尔曼秩相关系数。“秩”，可以理解成就是一种顺序或者排序，那么它就是根据原始数据的排序位置进行求解，这种表征形式就没有了求皮尔森相关性系数时那些限制。

首先对两个变量$(X,Y)$的数据进行排序，然后记下排序以后的位置$(X’,Y’)$，$(X’,Y’)$的值就称为秩次，$d_i$表示秩次差，$n$表示数据的个数。

1.简单理解为计算原数据在新排序中所处的排列位置的差值;

2.不会出现皮尔逊相关系数中分母为0而无法计算的情况；

3.由于异常值的秩次不会有明显的变化，所以对斯皮尔曼相关系数的影响也比较小。

3.肯德尔相关性系数【kendall】

也是一种秩相关系数，计算的对象是分类变量。

它的目标对象是有序的类别变量，比如名次、年龄段、肥胖等级(重度肥胖，中度肥胖、轻度肥胖、不肥胖)等。它可以度量两个有序变量之间单调关系强弱。肯德尔相关系数使用了“成对“这一概念来决定相关系数的强弱。

成对可以分为一致对(Concordant)和分歧对(Discordant)。一致对是指两个变量取值的相对关系一致，可以理解为$X_2-X_1$与$Y_2-Y_1$有相同的符号；分歧对则是指它们的相对关系不一致，$X_2-X_1$与$Y_2-Y_1$有着相反的符号。

肯德尔系数有两个计算公式，一个是Tau-a，另一个是Tau-b。两者的区别是Tau-b可以处理有相同值的情况，即并列(tied ranks)。下面依次来介绍这两个公式。

下面通过一个例子来理解：

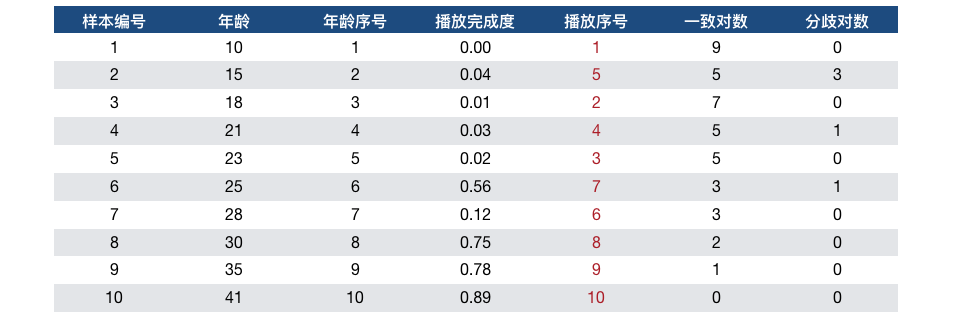
先来看一下一致对数和分歧对数是如何得出的。以样本6为例，样本6的年龄和播放完成度，分别小于样本8、9、10的年龄和播放完成度，因此有3个一致对数。样本6的年龄小于样本7的年龄，但播放完成度却大于样本7的，所以有一个分歧对数。汇总上面的表格，得出共有40个一致对数，有5个一致对数，所以Tau-a =$\frac{40-5}{40+5}$=0.778。

先来看一下一致对数和分歧对数是怎么得出来的。以样本1为例，它的年龄段序号和有效播放序号都小于6、8、9、10这几个样本对应的数值，因此一致对数为4。它的分歧对数为0。汇总共有21个一致对数，0个分歧对数。

首先，看一下$a_i=a_j$且$b_i=b_j$有几种情况：样本1、2、3符合这样的情况，样本4、5、7同样满足，样本8、9也满足，所以共有$\frac{3\ast (3-1)}{2}+\frac{3\ast (3-1)}{2}+\frac{2\ast (2-1)}{2}$=7;

$a_i=a_j$的数量，有样本1、2、3，样本4、5、7、6，样本8，9，所以共有：
$$\frac{3\ast (3-1)}{2}+\frac{4\ast (4-1)}{2}+\frac{2\ast (2-1)}{2}-7=3$$
同理，$b_i=b_j$的数量，有样本1、2、3、4、5、7共6种，6、8、9、10共4种，所以共有：
$$\frac{6\ast (6-1)}{2}+\frac{4\ast (4-1)}{2}-7=14$$
根据Tau-b的公式，有:
$$\frac{21}{\sqrt{21+321+14}}=0.725$$
通过上面的例子，我们可以看出，根据是否有重复值，要选择不同的公式。

4. 代码实现

DataFrame对象corr()方法的用法，该方法用来计算DataFrame对象中所有列之间的相关系数（包括pearson相关系数、Kendall Tau相关系数和spearman秩相关）。

DataFrame.corr(method='pearson', min_periods=1) 

参数说明：

method：可选值为{‘pearson’, ‘kendall’, ‘spearman’}

pearson：Pearson相关系数来衡量两个数据集合是否在一条线上面，即针对线性数据的相关系数计算，针对非线性数据便会有误差。

kendall：用于反映分类变量相关性的指标，即针对无序序列的相关系数，非正态分布的数据。

spearman：非线性的，非正太分析的数据的相关系数。