B样条（BSpline）曲线简介

大家好，欢迎来到IT知识分享网。

一、Bezier曲线的缺点

在正式开始介绍B-Spline之前，咱们先来聊聊贝塞尔曲线的缺陷。可参考：贝塞尔曲线简介-CSDN博客

（1）任何一控制点的变化会引起曲线上所有点的改变，牵一发而动全身。所以，贝塞尔曲线是无法针对局部进行编辑的。

（2）样条阶数和控制点个数成正比，随着控制点的增加，计算量会快速增加。所以随着Bezier曲线的阶数增加，对于曲线形状的控制将变得困难。主流的图形套件所提供的贝塞尔曲线接口很少超过3阶。

（3）确定了多边形的顶点数（m个），也就决定了所定义的Bezier曲线的阶次（m-1次），控制的自由度较少。

这些缺点决定了，如果我们需要用贝塞尔曲线作为唯一工具去绘制一个较为复杂的图形，为了保证可编辑性和渲染效率，只能将整个结构拆分成很多小段，用低阶数(主要是2阶）的贝塞尔曲线进行拟合，再进行拼接。

二、B样条曲线

简单说来，B条就是分段连续多项式，而且在全曲线上有限阶可导/连续。

B样条（B-Spline）是对贝塞尔曲线的一般化，它的诞生时为了解决Bezier在应用过程中暴露出的一系列缺陷。为了实现对曲线更好的控制力，B-Spline对控制点和阶数做了解耦，两者再无直接关系，并且引入了节点向量（Knots）。相比于贝塞尔曲线只有控制点一个自由度，B-spline拥有的自由度多达三个。

B样条的整条曲线有一个完整的表达形式，在有限阶内都十分平滑，完全可以符合人的直观审美，但内在的量却是分段的。如此一来，既克服了波动现象，曲线又是低次的，既有统一的表达式，又有统一的算法。B样条能够分段的根本，在于其基函数的局部性。

1、B样条的定义

B样条表达式与贝塞尔曲线十分相似，最大的区别就是基函数的不同。下标由伯恩斯坦基函数的n变为B样条基函数的k，表示B样条的多项式的次数和控制顶点的数目是没有关系的，而是由使用者自定义的。B样条的表达式为：

$P(u)=\sum_{i=1}^{n}P_{i}B_{i,k}(u)$

其中，Pi为n个控制顶点，Bik(u)称为k阶（k-1次）B样条基函数。k用以刻画阶次，可以是2到n+1之间的任意整数。对于贝塞尔曲线来说，阶数和次数是一样的，都是n。但对于B样条，阶数k就是次数k-1加1，和n无关。B样条基函数是一个称为节点矢量的非递减参数u的序列所决定的k阶分段多项式，这个序列就称为节点向量。

$u_{1},u_{2},u_{...},u_{n-1},u_{n},u_{n+1},u_{...},u_{n+k-1},u_{n+k}$

因此B样条基函数实际上就是一个多项式。那么如何得到这个B样条基函数？B样条基函数可以有各种各样的定义方式，但公认的最容易理解的，且应用最广泛的是De Boor Cox递推定义。它的原理是，对于k阶（k-1次）的B样条基函数，构造一种递推的公式：由0次构造1次，1次构造2次，2次构造3次，以此类推。

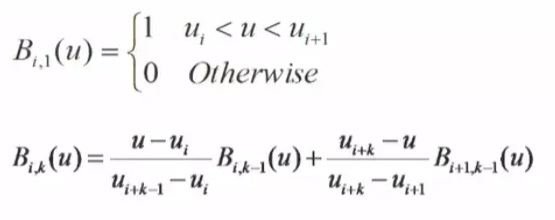
递推公式表明，若确定第i个k阶B样条基函数Bik(u)，需要用到[ui,ui+1…ui+k]共k+1个节点，称为区间[ui,ui+k]为此基函数Bik(u)的支撑区间。在此约定0/0=0。根据公式，u在计算过程中被归一化了，所以基函数仅与各个节点之间的相对距离有关，与u的绝对大小无关，取u=[0,1,2,3,4,5]和u=[0,0.2,0.4,0.6,0.8,1]效果是相同的。

2、k阶B样条基函数对应节点向量的数量

假设控制顶点P的数量为n个（1-n计序）：

对于Bi1(u)(1阶0次基函数)来说，涉及[ui,ui+1]一个区间，两个节点；

对于Bi2(u)(2阶1次基函数)来说，是由Bi1(u)和B(i+1)1(u)组成的，因此Bi2(u)涉及[ui,ui+1]，[ui+1,ui+2]，也即[ui,ui+2]两个区间三个节点；以此类推，对于Bik(u)涉及[ui,ui+k]，k个区间k+1个节点；因此，Bnk(u)涉及[un,un+k]。所以对于整个B样条来说，全部节点向量中的节点数一共是n+k个节点。

$u_{1},u_{2},u_{...},u_{n-1},u_{n},u_{n+1},u_{...},u_{n+k-1},u_{n+k}$

3、B样条基函数的定义区间

有个一直比较模糊的事，就是u的定义区间，我们知道u是代替了贝塞尔曲线中的t，而t有明确的区间0到1，而对于u来说，我们只关系将u的定义区间用节点画成了几份。u的定义区间到底是什么？其实前面说了。u的定义区间本身并不重要的原因是在计算过冲中归一化过，故基函数仅与各个节点之间的相对距离有关，与u的绝对大小无关。取u=[0,1,2,3,4,5]和u=[0,0.2,0.4,0.6,0.8,1]效果是相同的。为了方便起见，一般都默认u取值区间和t一样，也是定义在0到1。相比取值区间，更重要的在于，B样条基函数更依赖于节点向量的相对分布情况。根据节点的分布情况的不同，B样条有不同的类型。

4、B样条曲线类型的划分

（1）均匀型B样条

当节点沿参数轴均匀等距分布时，即u(i+1)-u(i)=常数时，为均匀b样条函数。均匀型B样条的基函数呈周期性，给定n和k，所有的基函数都有相同的形状。每个后续基函数仅仅是前面基函数在新位置上的重复。有的教材称为其顺序节点方法。注意的是，u的总点数是不变的，为n+k。（假设n=8，k=3，则u为11个点）

（2）准均匀型B样条

准均匀B样条与均匀型的差别，在于两端节点具有重复度k。不像贝塞尔曲线，均匀B样条曲线无法过两个端点，而准均匀B样条曲线则有效保留了过两个端点的性质。有的教材称其为Clamped方法。注意的是，u的总点数是不变的，为n+k。（假设n=8，k=3，则为11个点）

（3）分段贝塞尔曲线

节点矢量中两端节点具有重复度k，所有内节点重复度为k-1，这样的节点矢量定义了分段的伯恩斯坦基。即贝塞尔曲线可以看做B样条曲线的一个特例。此B样条曲线由分段的贝塞尔曲线拼接而成。因此各段就有了相对的独立性，克服了贝塞尔曲线的不足。B样条用分段贝塞尔曲线表示后，各曲线线段就有了相对的独立性，另外，关于贝塞尔曲线一整套简单有效的算法都可以直接应用于此方法。其缺点则是较大地增加了定义曲线的数据，控制顶点及节点数。注意的是，u的总点数是仍为n+k，并且需要满足n-1是k-1的整数倍。（n=8，k=3不满足条件，改为n=9，则u为12个点）

三、BSpline的MATLAB代码

以下是使用matlab绘制的均匀B样条曲线脚本。

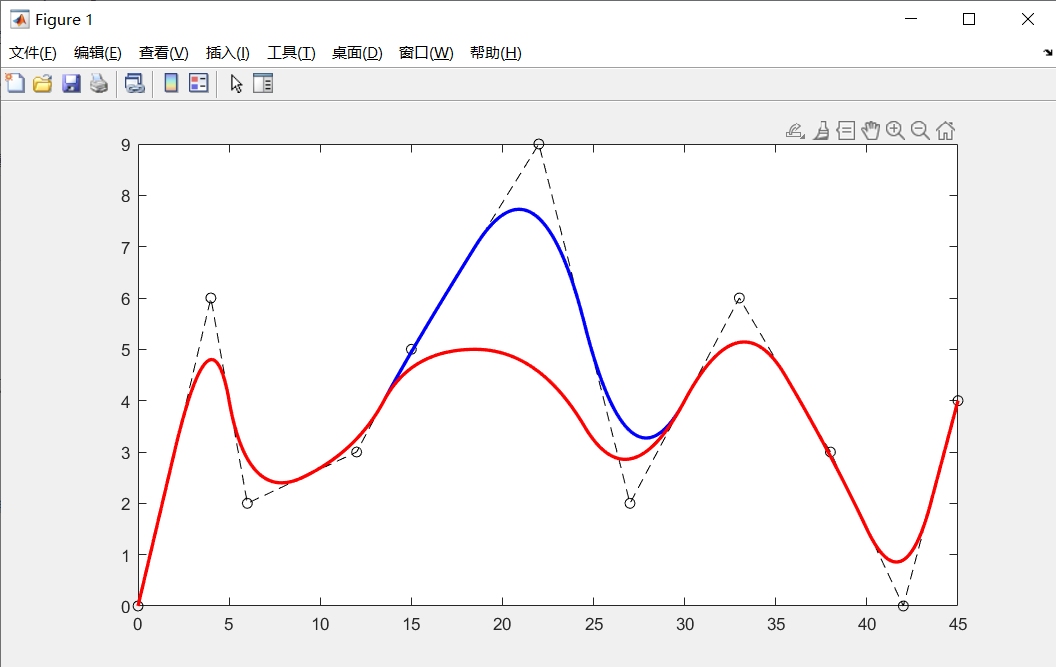
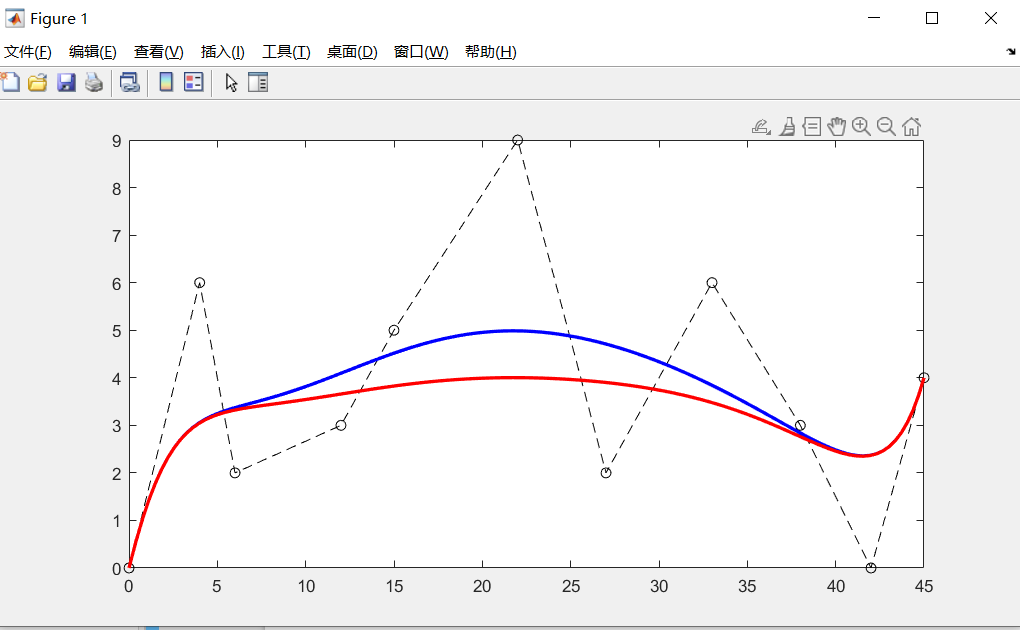
clc; clear; close; % 控制点序列P P = [0,0; 4,6; 6,2; 12,3; 15,5; 22,9; 27,2; 33,6; 38,3; 42,0; 45,4]; % P2为修改P一个点 P2 = P; P2(6,2) = 5; plot(P(:,1),P(:,2),'k--o');hold on; BSpline(P,3,'b-',2); BSpline(P2,3,'r-',2); % B样条曲线的类型 function [C]=BSpline(varargin) narginchk(1,7); ctrls = varargin{1}; k = varargin{2}; line_type= varargin{3}; lw = varargin{4}; n = size(ctrls,1); weights = ones(n,1) / n; NodeVector = linspace(0, 1, n+k); % 均匀B样条的节点矢量，n个控制点，k阶B样条，n+k个节点 C = BSpline_gen(ctrls, n, k, NodeVector, 0.001, weights); plot(C(:,1),C(:,2),line_type,LineWidth=lw); end function [C]=BSpline_gen(ctrls,n,k,NodeVector,accuracy,weights) Bik_w = zeros(1,n); num = 1 / accuracy; C = zeros(num+1, 2); idx = 1; for u = 0 : accuracy : num * accuracy Dom = 0; for i = 1:n Bik_w(1,i) = BaseFunction(i, k, u, NodeVector) * weights(i,1); % 不同点的权重 Dom = Dom + Bik_w(1,i); end C(idx,:) = (Bik_w / Dom) * ctrls; idx = idx + 1; end end % 计算基函数Bik_u,NodeVector为节点向量 function Bik_u = BaseFunction(i, k , u, NodeVector) if k == 1 % 1阶0次B样条 if NodeVector(i) <= u && u < NodeVector(i+1) Bik_u = 1.0; else Bik_u = 0.0; end else % 支撑区间的长度 Length1 = NodeVector(i+k-1) - NodeVector(i); Length2 = NodeVector(i+k) - NodeVector(i+1); % 规定0/0 = 0 if Length1 == 0.0 Length1 = 1.0; end if Length2 == 0.0 Length2 = 1.0; end %递归计算 Bik_u = (u - NodeVector(i)) / Length1 * BaseFunction(i, k-1, u, NodeVector) ... + (NodeVector(i+k) - u) / Length2 * BaseFunction(i+1, k-1, u, NodeVector); end end

若再使用Bezier曲线进行拟合，则有

可以看到，改动了一个控制点，BSpline曲线受到影响的范围比Bezier曲线是要小的（控制点是我随意选取的，主要关注曲线的前后变化，拟合效果不是此次重点！），实现了对曲线更好的控制力。

关于Bezier曲线的原理和绘制代码参考博文：贝塞尔曲线简介-CSDN博客。关于B样条的性质等介绍，此处就不详述了。具体介绍可去参考链接处查阅。

参考链接：

（1）https://zhuanlan.zhihu.com/p/

（2）https://www.zhihu.com/question//answer/

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/128831.html