大家好,欢迎来到IT知识分享网。
目录
一、二进制简单介绍
1、二进制与十进制的计算对比
2、常用二进制转十进制的转换关系
| 二进制 | 十进制 |
|---|---|
| 0001 | 1 |
| 0010 | 2 |
| 0100 | 4 |
| 1000 | 8 |
表格展示
| 关注二进制1所在的位置 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 二进制 | 0001 | 0010 | 0100 | 1000 |
| 十进制 | 1 | 2 | 4 | 8 |
| 与二的次方的关系 | 20 | 21 | 22 | 23 |
二、二进制转十进制
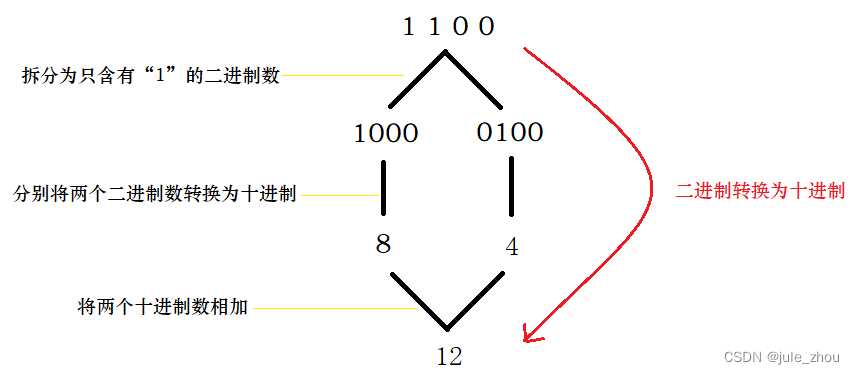
例如二进制1100转十进制
- 将1100拆分为只有一个数字“1”的情况,我们将会得到两个二进制数,分别为1000和0100
- 这两个数对应的十进制数为8和4,此时将这两个数按照十进制规则相加得到12
- 那么此时就可以知道,1100转换十进制的结果为12
下面通过图来解释。
三、十进制转二进制
首先让我们回顾以下二进制只有一个1的转换十进制的情况
| 二进制 | 十进制 |
|---|---|
| 1 | 1 |
| 10 | 2 |
| 100 | 4 |
| 1000 | 8 |
| 10000 | 16 |
| 32 | |
| 64 | |
| 128 |
十进制转二进制的时候
- 首先,将十进制数减去一个能减去的最大的2的自然数次方(即:2自然数,例如,20,215,…)得到一个正数的结果
- 然后再用这个结果继续减去一个能减去的最大的2的自然数次方
- 以此类推,知道结果为0时结束
- 在此过程中使用的自然数从大到小依次排列写为“1”,未使用的记为“0”
四、二进制的简单运算
1、运算符&,简称“与”
- 二进制数最后一个数对齐(即十进制中的个位),其他数依次对其,缺少的部分补为“0”.
- 分别看对其的数
- 两个数均为“1”,则最终结果计算为“1”,否则 为“0”.
通过该方法得到一个新的二进制数,即为计算结果 十进制数做位运算时,需要转化为二进制计算
2、运算符|,简称“或”
1010 | 0110 = 1110 (用十进制表达,即为:10 | 8 = 14)
进行二进制“或”计算时,
- 二进制数最后一个数对齐(即十进制中的个位),其他数依次对其,缺少的部分补为“0”.
- 分别看对其的数
- 两个数有一个为为“1”,则最终结果计算为“1”,否则 为“0”.
3、运算符!,简称“非”
!1010 = 0101 (用十进制表达,即为:!10 = 5)
进行二进制“非”计算时,
- 二进制数为“0”,计算结果为“1”
- 二进制数为“1”,计算结果为“0”
4、运算符~,简称“取反”
5、运算符^,简称“异”
五、二进制的位运算
1、左移“<<”
<< 表示左移,不分正负数,低位补0;
如:0010 <<1 = 001(即:2<<1 = 1)可以看作:2 * 21 = 4
1010 << 2 = 10(即:10<<2 = 2)可以看作:10 * 22 = 40
-10<<2 = -40(即:-10<<2 = 2)可以看作:-10 * 22 = -40
-15<<2 = -60(即:-15<<2 = 2)可以看作:-15 * 22 = -60
相当于,每左移一位,对应的十进制数乘以2
2、右移“>>”
需要考虑最高位
“>>”表示右移,如果该数为正,则高位补0,若为负数,则高位补1;
如:0010 >> 1 = 001(即:2>>1 = 1)可以看作:2 / 21=1
1010 >> 2 =10(即:10>>2=2)可以看作:10 / 22 = 2
相当于,每右移一位,对应的十进制数整除2
-10>>2 = -3(即:-10>>2 = -3)可以看作:-10 / 22 – 1 = -3
-15>>2 = -4(即:-15>>2 = -4)可以看作:-15 / 22 – 1 = -4
相当于,每右移一位,对应的十进制数整除2再减去1
3、无符号左移“<<<”
左移运算符是用来将一个数的各二进制位左移若干位,移动的位数由右操作数指定(右操作数必须是非负值),其右边空出的位用0填补,高位左移溢出则舍弃该高位。
4、无符号右移“>>>”
“>>>”表示无符号右移,也叫逻辑右移,即若该数为正,则高位补0,而若该数为负数,则右移后高位同样补0。
详细说明:
右移运算符是用来将一个数的各二进制位右移若干位,移动的位数由右操作数指定(右操作数必须是非负值),移到右端的低位被舍弃,对于无符号数,高位补0。对于有符号数,某些机器将对左边空出的部分用符号位填补(即“算术移位”),而另一些机器则对左边空出的部分用0填补(即“逻辑移位”)。注意:对无符号数,右移时左边高位移入0;对于有符号的值,如果原来符号位为0(该数为正),则左边也是移入0。如果符号位原来为1(即负数),则左边移入0还是1,要取决于所用的计算机系统。有的系统移入0,有的系统移入1。移入0的称为“逻辑移位”,即简单移位;移入1的称为“算术移位”。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/129156.html