大家好,欢迎来到IT知识分享网。
2.1 概述因子分析(FA)是一种探索性数据分析方法,将存在某些相关性的变量提炼为较少的几个因子,用这几个因子去表示原本的变量,也可以根据因子对变量进行分类。 2.2 因子分析的前提条件1、数据中没有异常值。 2、样本数量应大于因子。 3、不能有完美的多重共线性。 4、变量之间不应有同调性。 2.3 因子分析的类型探索性因素分析:它是社会和管理研究人员中最流行的因素分析方法。它的基本假设是,任何观察到的变量都与任何因素直接相关。 验证性因素分析(CFA):其基本假设是每个因素都与一组特定的观察变量相关联。CFA确认在此基础上的期望。 2.4 因子分析(FA)过程1、求解方程中的因子F的系数。 2、给予因子F实际的解释。 3、展示原始特征和公共因子之间的关系,从而实现降维和特征分类等目的。 注意:求解方程的过程,就是分析变量的相关系数矩阵,从而找到少数几个随机变量去描述所有变量;又因为求解的不唯一性,最后通常会对因子的载荷矩阵做一次正交旋转,为了:方便理解每个因子的意义。 2.5 因子分析实操步骤1、充分性检验 目的:检验变量之间是否存在相关性,从而判断是否适合做因子分析。 方法:抽样适合性检验(KMO检验)或者巴特利特检验(Bartlett’s Test) 2、选择因子个数 目的:通过数据定义最合适的潜在公共因子个数,这个决定后面的因子分析效果。 方法:Kaiser”s准则或者累积贡献率原则。 3、提取公共因子并做因子旋转 提取公共因子就是上面提到的求解函数的过程,一般求解方法有:主成分法、最大似然法、残差最小法等等; 因子旋转的原因是提取公共因子的解有很多,而因子旋转后因子载荷矩阵将得到重新分配,可以使得旋转后的因子更容易解释。常用的方法是:方差最大法。 4、对因子做解释和命名 目的:解释和命名其实是对潜在因子理解的过程;这一步非常关键,需要非常了解业务才可。这也是我们使用因子分析的主要原因。 方法:根据因子载荷矩阵发现因子的特点。 5、计算因子得分 对每一样本数据,得到它们在不同因子上的具体数据值,这些数值就是因子得分。 |
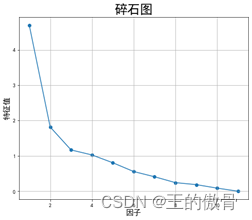
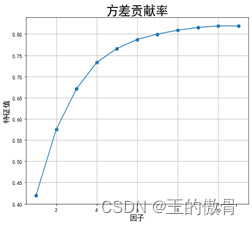
街区普查数据案例分析Step1:数据预处理和分析: 新增“人口密度”特征,删除特征人口量、面积、经度和维度。 Step2:因子分析——充分性检验 巴特利特P值小于0.05,KMO值大于0.5;说明此数据不太适合做因子分析。(数据给的不合适) Step3:因子个数确定 特征值大于1的因子数有4个,且两个因子的累计方差有73%;因此确定因子个数为4个。 |
|
碎石图与方差贡献率 |
|
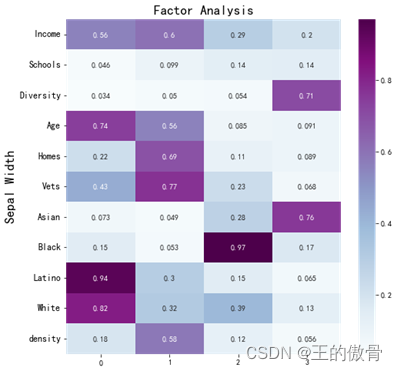
做因子分析 调用因子分析函数,并得到因子载荷矩阵;从载荷矩阵可以看到,第一个因子与年龄、欧裔比例呈正相关。第二个因子与收入、复原军人比例、有房家庭比例呈正相关。第三个因子与种族多样性、亚裔人口比例呈正相关。 |
|
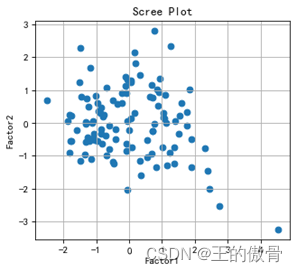
Step5:计算因子得分 |
|
优缺点评价: 优点 1、不是对原有变量的取舍,而是根据原始变量的信息进行重新组合,找出影响变量的共同因子,化简数据。 2、通过旋转使得因子变量更具有可解释性,命名清晰性高。 缺点 |
3、在计算因子得分时,采用的是最小二乘法,此法有时可能会失效。
Python中街区普查案例代码(FA)
1. import pandas as pd 2. import numpy as np 3. import matplotlib.pyplot as plt 4. from sklearn.preprocessing import StandardScaler 5. import matplotlib 6. 7. LA_data = pd.read_csv("LA.Neighborhoods.csv") 8. LA_data 9. # 新增人口密度,去掉人口量、面积、经度和维度 10. LA_data["density"] = LA_data["Population"]/LA_data["Area"] 11. LA_data_final = LA_data.drop(["Population","Area","Longitude","Latitude"],axis=1) 12. LA_data_final_feat = LA_data_final.drop(['LA.Nbhd'],axis=1) 13. LA_data_final_feat 14. 15. #数据标准化 16. f = StandardScaler().fit_transform(LA_data_final_feat) # 数据标准化 17. f = pd.DataFrame(f) 18. 19. #计算巴特利特P值 20. from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity 21. chi_square_value,P_value = calculate_bartlett_sphericity(f) 22. chi_square_value,P_value 23. #计算KMO 24. from factor_analyzer.factor_analyzer import calculate_kmo 25. kom_all,kmo_model = calculate_kmo(f) 26. kom_all,kmo_model 27. 28. from factor_analyzer import FactorAnalyzer 29. fa = FactorAnalyzer(LA_data_final_feat.shape[1]+1,rotation=None) 30. fa.fit(LA_data_final_feat) 31. ev,v = fa.get_eigenvalues() # 计算特征值和特征向量 32. var = fa.get_factor_variance()#给出方差贡献率 33. print('\n相关矩阵特征值:', ev) 34. matplotlib.rcParams["font.family"] = "SimHei" 35. plt.figure(figsize=(8, 6.5)) 36. plt.scatter(range(1, f.shape[1]+1), ev) 37. plt.plot(range(1, f.shape[1]+1), ev) 38. plt.title('碎石图', fontdict={'weight': 'normal', 'size': 25}) 39. plt.xlabel('因子', fontdict={'weight': 'normal', 'size': 15}) 40. plt.ylabel('特征值', fontdict={'weight': 'normal', 'size': 15}) 41. plt.grid() 42. plt.show() 43. 44. print('\n方差贡献率:', var) 45. matplotlib.rcParams["font.family"] = "SimHei" 46. plt.figure(figsize=(8, 6.5)) 47. plt.scatter(range(1, f.shape[1]+1), var[2]) 48. plt.plot(range(1, f.shape[1]+1), var[2]) 49. plt.title('方差贡献率', fontdict={'weight': 'normal', 'size': 25}) 50. plt.xlabel('因子', fontdict={'weight': 'normal', 'size': 15}) 51. plt.ylabel('特征值', fontdict={'weight': 'normal', 'size': 15}) 52. plt.grid() 53. plt.show() 54. 55. fa = FactorAnalyzer(4,rotation="varimax") 56. fa.fit(LA_data_final_feat) 57. df_loading = pd.DataFrame(fa.loadings_,index=LA_data_final_feat.columns.tolist()) 58. # 输出载荷矩阵 59. df_loading 60. 61. # 对系数矩阵进行可视化 62. import seaborn as sns 63. df_cm = pd.DataFrame(np.abs(fa.loadings_),index=df_loading.index) 64. plt.figure(figsize = (8,8)) 65. ax = sns.heatmap(df_cm, annot=True, cmap="BuPu") 66. # 设置y轴的字体的大小 67. ax.yaxis.set_tick_params(labelsize=12) 68. plt.title('Factor Analysis', fontsize='xx-large') 69. # Set y-axis label 70. plt.ylabel('Sepal Width', fontsize='xx-large') 71. #plt.savefig('factorAnalysis.png', dpi=200) 72. 73. #计算因子得分 74. LA_data_trans = pd.DataFrame(fa.transform(LA_data_final_feat),index=LA_data_final["LA.Nbhd"]) 75. LA_data_trans 76. 77. #以散点图的形式呈现 78. matplotlib.rcParams["font.family"] = "SimHei" 79. matplotlib.rcParams['axes.unicode_minus']=False 80. plt.figure(figsize = (10,4),dpi = 80) 81. plt.subplot(1,2,1) 82. plt.scatter(LA_data_trans.loc[:,0],LA_data_trans.loc[:,1]) 83. plt.title("Scree Plot") 84. plt.xlabel("Factor1") 85. plt.ylabel("Factor2") 86. plt.grid() 免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/129747.html