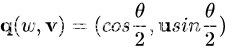轴角、四元数转换

大家好，欢迎来到IT知识分享网。

轴角：

轴角用一个以单位矢量定义的旋转角，再加上一个标量定义的旋转角来表示旋转。通常的表示[x,y,z,theta]，前面三个表示轴，最后一个表示角度。表示非常直观，也很紧凑。

四元数：

四元数（Quaternions）是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865）在1843年发明的数学概念。四元数的乘法不符合交换律（commutative law）。

明确地说，四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。

四元数—>轴角

const q = { w: 0.88882, x: 0, y: 0, z: 0.88854 } // 轴角 43.065 let angle = 0 const siny_cosp = 2 * (q.w * q.z + q.x * q.y) // Math.pow(q.z, 2)=q.z*q.z const cosy_cosp = 1 - 2 * (Math.pow(q.y, 2) + Math.pow(q.z, 2)) //弧度 const radian = Math.atan2(siny_cosp, cosy_cosp) // 角度 angle = radian * 180 / Math.PI console.log('43.065:', angle) 

轴角—> 四元数

 // 绕z轴旋转角度 ，单位向量为[0,0,1] // 角度写法 ：vAngle = angle/2*Matn.PI/180 // 弧度写法 ：vAngle = radian/2 // radian= angle * Math.PI / 180 const vAngle = radian/ 2 const q2 = { x: 0 * Math.sin(vAngle), y: 0 * Math.sin(vAngle), z: 1 * Math.sin(vAngle), w: Math.cos(vAngle) 

样例

<script> test() function test() { 
    const coordinate={ 
    x:0.03144, y:-2.7007, z:0 } const q = { 
    x:0, y:0, z:0.44386, w:0.00001 } const uAngle =120 // 轴角 43.065 let angle = 0 const siny_cosp = 2 * (q.w * q.z + q.x * q.y) // Math.pow(q.z, 2)=q.z*q.z const cosy_cosp = 1 - 2 * (Math.pow(q.y, 2) + Math.pow(q.z, 2)) //弧度 const radian = Math.atan2(siny_cosp, cosy_cosp) // 角度 angle = radian * 180 / Math.PI console.log("radian:", radian) console.log(uAngle,":", angle) // 角度写法 ：vAngle = angle/2*Matn.PI/180 // 弧度写法 ：vAngle = radian/2 // radian= angle * Math.PI / 180 //坐标在xy平面上，绕轴即为z，向量值即为{x:0,y:0,z:1} const q2 = { 
    x: 0 * Math.sin(radian/ 2), y: 0 * Math.sin(radian/ 2), z: 1 * Math.sin(radian/ 2), w: Math.cos(radian/ 2) } console.log(q, q2) } </script>