大家好,欢迎来到IT知识分享网。
第一章 绪论
1.1 什么是算法
算法(algorithm)是一系列解决问题的明确指令,也就是说,对于符合一定规范的输入,能够在有限时间内获得要求的输出。
观点:可以认为算法是问题的程序化解决方案。
1.2 算法的描述
伪代码(pseudocode) 是自然语言和类编程语言组成的混合结构。伪代码往往比自然语言更精确,而且用伪代码描述的算法往往会更简洁。用箭头代表赋值操作。
1.3 算法的分析
效率有两种
- 时间效率(time efficiency),指出算法运行有多快。
- 空间效率(space efficiency),说明算法需要多少额外的存储空间。
1.4重要的问题类型
- 排序问题(sorting problem):要求我们按照升序重新排列给定列表中的数据项。
- 查找问题(searching problem):就是在给定的集合(或者是多重集,它允许多个元素具有相同的值)中找一个给定的值[我们称之为查找键(search key)]。
- 字符串处理,也称字符串匹配问题
- 图问题
- 组合问题
- 几何问题:类似于点、线、多面体这样的几何对象。
- 数值问题(numerical problem):是另一个广阔的具体应用领域,涉及具有连续性的数学问题:像解方程和方程组,计算定积分以及求函数的值等。
第2章 算法效率分析基础
不做笔记
第3章 蛮力法
蛮力法(brute force)是一种简单直接地解决问题的方法,常常直接基于问题的描述和所涉及的概念定义。
3.1 选择排序和冒泡排序
3.1.1选择排序
3.1.2 冒泡排序
3.2 顺序查找和蛮力字符串匹配
3.2.1 顺序查找
该算法只是简单地将给定列表中的连续元素和给定的查找键进行比较,直到遇到一个匹配的元素(成功查找),或者在遇到匹配元素前就遍历了整个列表(失败查找)。
实现顺序查找时常常会使用这样一个小技巧:如果我们把查找键添加到列表的末尾,那么查找就一定会成功,所以不必在算法的每次循环时都检查是否到达了表的末尾。以下是这个增强版本的伪代码。
3.2.2蛮力字符串匹配
查找字符串第一个字符的位置
请注意,在这个例子中,几乎每做一次字符比较就要移动一次模式的位置。然而,最坏的情况比这还要糟得多:在移动模式之前,算法可能会做足m次比较,而n-m+1次尝试的每一次都可能会遇到这种情况。因此,在最坏的情况下,该算法属于O(nm)。
3.3 最近对和凸包问题的蛮力算法
3.3.1 最近问题
最近点对问题要求在一个包含n个点的集合中,找出距离最近的两个点。这种处理平面或者高维空间的邻近点的问题,在各种计算几何问题当中是最简单的。最近点对问题的一个最重要的应用是统计学中的聚类分析。
3.3.2 凸包问题
3.4 穷举查找
对于组合问题来说,穷举查找(exhaustive search)是一种简单的蛮力方法。它要求生成问题域中的每一个元素,选出其中满足问题约束的元素,然后再找出一个期望元素(例如,使目标函数达到最优的元素)。 注意,虽然穷举查找的思想很简单直接,但在实现时,它常常会要求算法来生成某些组合对象。
常见问题
- 旅行商问题
- 背包问题
- 分配问题
3.5深度优先查找和广度优先查找
3.5.1 深度优先查找
3.5.2 广度优先查找
第4章 减治法
4.1 插入排序
我们考虑如何用减一技术对一个数组A[0.-1]排序。遵循该方法的思路,我们假设对较小数组A[0.n-2]排序的问题已经解决了,得到了一个大小为n-1的有序数组:A0]≤…≤[n-2]。我们如何利用这个较小规模的解,并将元素A[n-1]考虑进来,来得到原问题的解呢?显然,我们需要做的就是在这些有序的元素中为A[-1]找到一个合适的位置,然后把它插入到那里。一般来说,我们可以从右到左扫描这个有序的子数组,直到遇到第一个小于等于A[-1]的元素,然后把A[n-1]插在该元素的后面。这种算法被称为直接插入排序(straight insertion sort),或者简称为插入排序(insertion sort)。
4.2 拓扑排序
4.3生成祝贺对象的算法
4.4 减常因子算法
以上略,有时间再做笔记
4.4.1 折半查找
对于有序数组的查找来说,折半查找是一种性能卓越的算法。它通过 比较查找键K和数组中间元素A[m] 来完成查找工作。如果它们相等,算法结束。否则,如果K<A[m],就对数组的前半部分执行该操作,如果K>A[m],则对数组的后半部分执行该操作。
4.4.2 假币问题
4.4.3 俄式乘法
4.4.4 约瑟夫斯问题
== 三问题略==
4.5减可变规模算法
4.5.1 插值查找
有时间再做笔记
第五章 分治法
基本思想:
将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且原问题相同。递归地解这些子问题,然后将各子问题的解合并得到原问题的解。
精髓:
分——将问题分解为规模更小的子问题。
治——将这些规模更小的子问题逐个击破。
合——将已解决的子问题合并,最终得到原问题的解。
5.1 合并排序
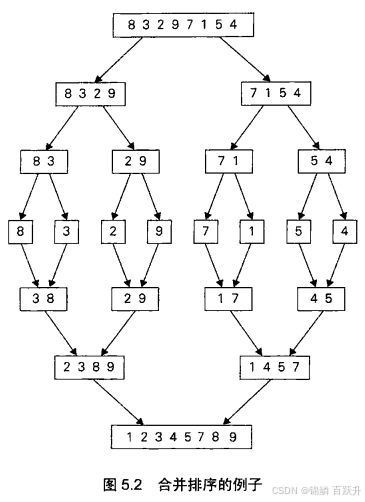
图5.2演示的是用合并排序算法对数列8,3,2,9,7,1,5,4进行排序的操作过程。
5.2 快速排序
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/129902.html