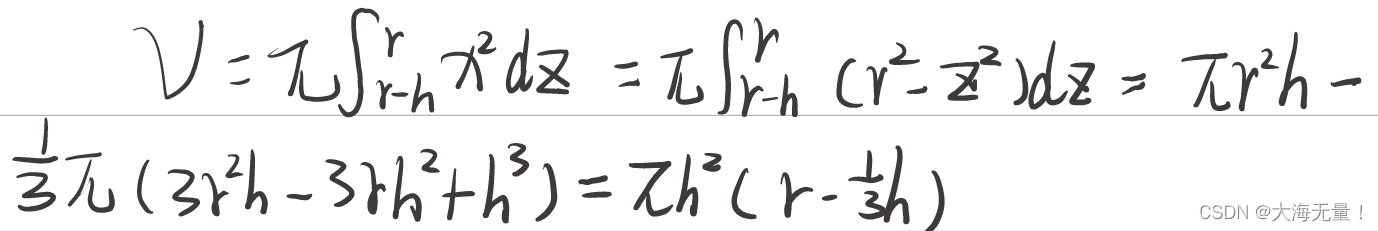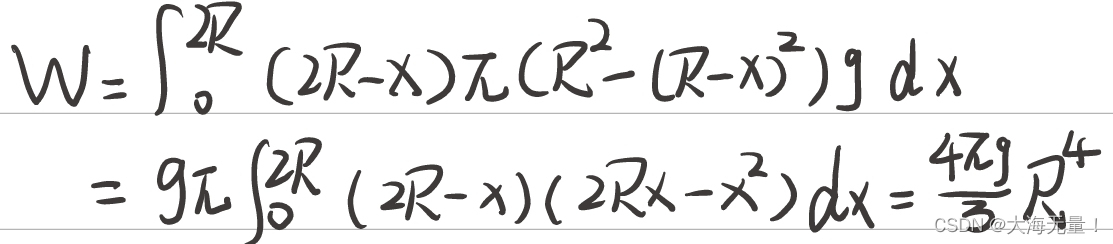大家好,欢迎来到IT知识分享网。
球缺的定义
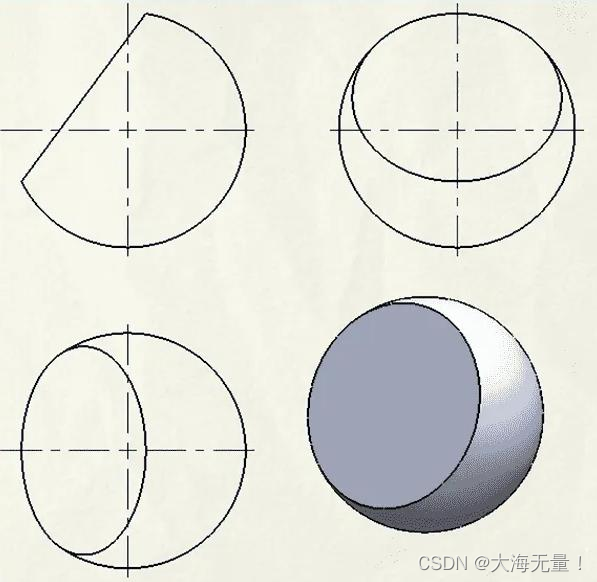
一个球被平面截下的一部分叫做球缺。截面叫做球缺的底面,垂直于截面的直径被截后被截下的线段长叫做球缺的高。
计算方法
对于计算立体的体积,我们有很多办法,比如定积分,二重积分,三重积分。在此我选用定积分来计算。
首先我们需要明确的是,球缺是需要我们指定的,球缺可以是上部分,也可以是下部分,取上部分为例子。
我们可以理解这个球体是由x=sqrt(r×r-z×z)绕着z轴旋转得到的,且(r-h<z<r),球缺高度为h。
因为我们变量为z,所以将x设为因变量。然后对z积分,即可求得结果。
典型例题
比如说下面的例题就可以很好的使用这个球缺公式!
一半径为R的球沉入水中,球面顶部正好与水面相切,球的密度为1,求将球从水中取出所做的功。 设球与水面切点为原点,X轴竖直向下,我们取x处一片高为dx的体积,根据微元化的思想,我们可以认为在dx内取得这一片体积是高度为dx的圆柱体,所以我们可以表示距原点x处的一片体积为V=π[R²-(R-x)²]dx,这部分重力G=π[R²-(R-x)²]gdx。
如果我们要想要将球完全提离水面,则每一片都要上拉2R的距离,但由于在水中上拉的时候,重力等于浮力,拉力不做功,直到这一小片体积脱离水面才开始做功。
所以它在空气中上升的距离即为做功的位移为2R-x,所以dw=(2R-x)π[R²-(R-x)²]gdx,对dw求积分即可得到所做的功。x的范围为(0,2R)。
如果有不对的地方,还望各位大佬指正!
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/130058.html