大家好,欢迎来到IT知识分享网。
白话向量点积
点积(Dot Product)是机器学习中最常见的向量操作。本文将通过简洁易懂的语言配合大量图形为大家介绍点积运算及其背后的数学意义。
背景知识
对于长度为 n n n 的两个向量 a a a 和 b b b,
a = [ a 1 , a 2 , a 3 , … , a n ] b = [ b 1 , b 2 , b 3 , … , b n ] \begin{aligned} a &= [a_1, a_2, a_3,\dots,a_n]\\ b &= [b_1, b_2, b_3,\dots,b_n] \end{aligned} ab=[a1,a2,a3,…,an]=[b1,b2,b3,…,bn]
点积可以用来表示它们之间的关系。 例如,它们指向同一个方向还是相反的方向? 它们彼此垂直吗?
两个向量进行点积运算的结果是标量,因此点积有时也称为标量积。
为了让大家建立对点积工作原理的直觉,我们从其几何定义开始。
几何视角
- ∥ a ∥ \Vert a \Vert ∥a∥: 向量 a a a 的大小
- ∥ b ∥ \Vert b \Vert ∥b∥: 向量 b b b 的大小
- θ \enspace\theta\enspace θ: 向量 a , b a,b a,b 之间的夹角
向量的大小
向量长度直观看上去就是一个用勾股定理计算斜边长度。对于二维向量来说就是 x 2 + y 2 \sqrt{x^2+y^2} x2+y2,对于三维向量来说就是 x 2 + y 2 + x 2 \sqrt{x^2+y^2+x^2} x2+y2+x2 。推而广之, n n n 维向量的长度为
∥ v ∥ = v 1 2 + v 2 2 + ⋯ + v n 2 \Vert v \Vert = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2} ∥v∥=v12+v22+⋯+vn2
Cosine
cos θ \cos\theta cosθ 将向量 a a a 投影到向量 b b b 。上图中,向量 a a a 和向量 b b b 指向不同方向,所以 ∥ a ∥ cos θ \Vert a \Vert \cos\theta ∥a∥cosθ 将向量 a a a 的一部分投影到向量 b b b 的方向上。反过来视为将向量 b b b 投影到向量 a a a 也可以,
举例
几何意义
上面的结果有什么意义呢?
我们都知道当两个向量指向相同方向时,它们之间的角度为 θ = 0 ° \theta = 0\degree θ=0° 或 0 0 0 弧度。 这意味着 cos ( θ ) \cos(\theta) cos(θ) 的结果为 1,此时点积最大。如果两个向量指向相反方向时,它们之间的角度为 θ = 180 ° \theta = 180\degree θ=180° 或 π \pi π 弧度。 这意味着 cos ( θ ) \cos(\theta) cos(θ) 的结果为 -1,此时点积最小。当 θ = 90 ° \theta = 90\degree θ=90° 或 π / 2 \pi/2 π/2 弧度时, cos ( θ ) \cos(\theta) cos(θ) 的结果为 0,此时点积为0。当点积为 0 时,意味着两个向量彼此垂直或正交。
| 方向关系 | 计算结果 | |
|---|---|---|
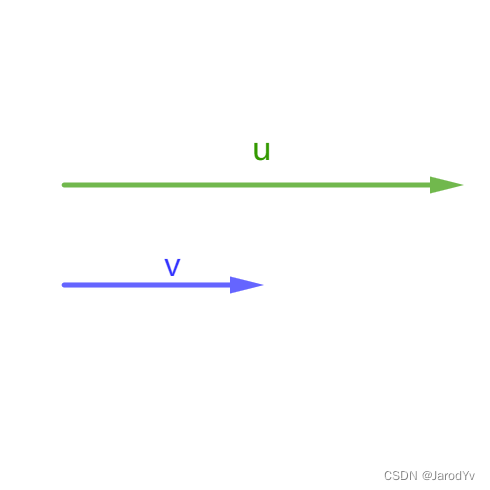 |
完全同向 | + A B +AB +AB |
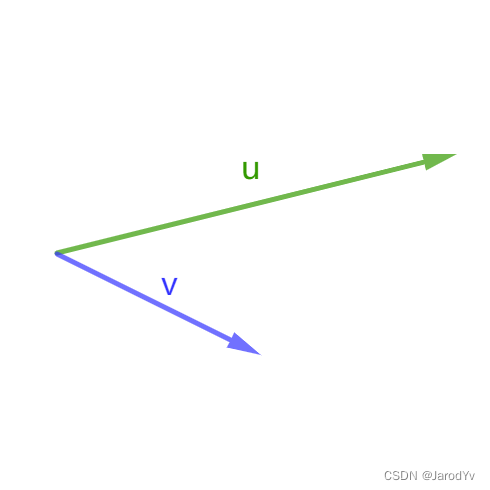 |
基本同向 | < + A B \lt +AB <+AB |
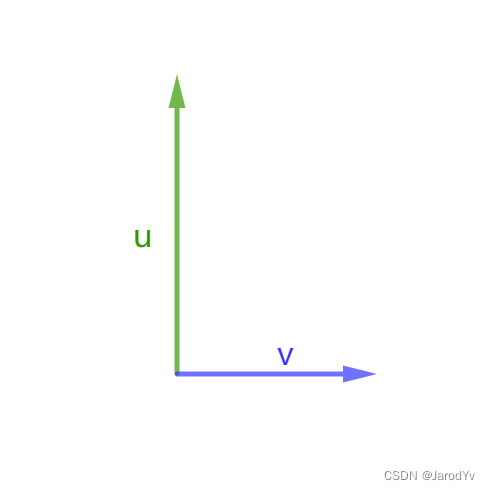 |
垂直 | 0 0 0 |
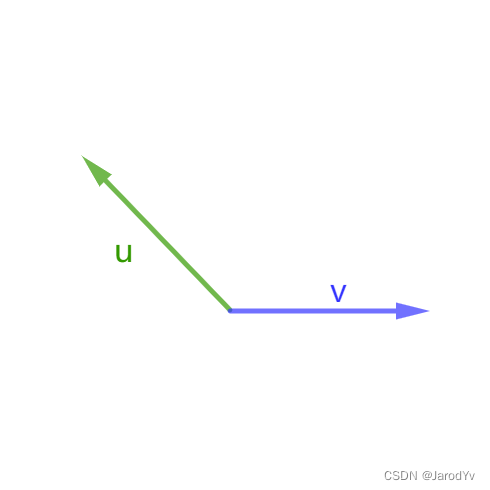 |
基本反向 | > − A B \gt -AB >−AB |
 |
完全反向 | − A B -AB −AB |
坐标视角
两种视角的等价性
标准基可以将任意向量分解为各分量与标准基的线性组合,比如三维空间中的向量 v v v 可以表示为:
v x e x + v y e y + v z e z v_xe_x+v_ye_y+v_ze_z vxex+vyey+vzez
其中 v x , v y , v z v_x, v_y, v_z vx,vy,vz 是向量 v v v 的分量。
点积的作用
- 物理中很多量都是矢量(既有大小也有方向),这些矢量可以通过点积连接。比如:
功 = ( 力 ⃗ ) ⋅ ( 距离 ⃗ ) \text{功} = (\vec{力}) \sdot (\vec{距离}) 功=(力)⋅(距离) - 可以计算两个向量的夹角,比如:
u ⃗ = ( 81 , − 15 ) v ⃗ = ( 22 , 37 ) 无需作图,通过代数形式可以计算得: u ⃗ ⋅ v ⃗ = 81 × 22 + ( − 15 ) × 37 = 1227 再根据几何形式有: ∥ u ∥ = 8 1 2 + ( − 15 ) 2 = 81.09 ∥ v ∥ = 2 2 2 + 3 7 2 = 43.05 ∥ u ∥ ∥ v ∥ = 3491 cos θ = u ⃗ ⋅ v ⃗ ∥ u ∥ ∥ v ∥ = 1227 3491 = 0. θ = cos − 1 ( 0. ) = 69.42 ° \vec{u} = (81, -15)\\ \vec{v} = (22, 37) \\ \text{无需作图,通过代数形式可以计算得:}\\ \vec{u}\sdot\vec{v} = 81 \times 22+(-15)\times37 =1227\\ \text{再根据几何形式有:}\\ \Vert u\Vert = \sqrt{81^2+(-15)^2} = 81.09\\ \Vert v\Vert = \sqrt{22^2+37^2} = 43.05\\ \Vert u\Vert \Vert v\Vert = 3491 \\ \cos\theta = \frac{\vec{u}\sdot\vec{v}}{\Vert u\Vert \Vert v\Vert} = \frac{1227}{3491} = 0. \\ \theta = \cos^{-1}(0.) = 69.42\degree u=(81,−15)v=(22,37)无需作图,通过代数形式可以计算得:u⋅v=81×22+(−15)×37=1227再根据几何形式有:∥u∥=812+(−15)2=81.09∥v∥=222+372=43.05∥u∥∥v∥=3491cosθ=∥u∥∥v∥u⋅v=34911227=0.θ=cos−1(0.)=69.42°
总结
点积是机器学习中最常见的向量操作。上面内容为了简单易懂可能在数学上有失严谨,全面严谨的讲解建议大家系统性地学习一下线性代数,这里推荐 Gilbert Strang 老爷子的 Introduction to Linear Algebra,这本书是我读过对初学者最友好的线性代数书。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/130164.html






