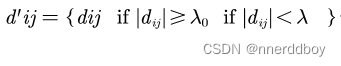白话机器学习4：小波分解的原理与Python代码实现

大家好，欢迎来到IT知识分享网。

        小波去噪可以想象成使用一把“筛子”来过滤信号。这个“筛子”能够根据信号的不同频率成分，将其分解成多个层次。在这个过程中，信号的重要信息通常包含在低频部分，而噪声则多分布在高频部分。

        将信号通过这个“筛子”分解后，我们可以对那些包含噪声的高频部分进行“削弱”或“切除”，然后再将剩下的部分重新组合起来。这样，经过处理的信号就会保留下重要的信息，同时去除了很多噪声。

一、数学原理详解

小波变换通过一系列可缩放（尺度变化）和平移的基函数来表示信号。这些基函数称为小波函数。

小波函数 具有一定的时间长度并集中在频率上，可以通过缩放（dilation）和平移（translation）来拟合信号的不同部分：

其中 a 是尺度参数，b 是平移参数。

分解:

信号f(t)可以通过小波函数的线性组合来分解：

其中是小波系数。

在实际操作中，通过离散小波变换DWT，我们可以得到信号在不同尺度和位置的小波系数。

去噪

小波去噪的步骤通常包括：

1. 选择小波基：选择一个适当的小波函数，比如Daubechies小波。
2. 多尺度分解：将信号进行多层分解，得到不同尺度上的小波系数。
3. 阈值处理：对小波系数应用阈值规则。系数小于某个阈值的被视为噪声并设置为零或减小其值。阈值的选择是一个关键步骤，常用的方法有软阈值和硬阈值。软阈值方法会对系数进行收缩，而硬阈值方法会直接将小于阈值的系数置为零。

   硬阈值: 

   软阈值:   

   其中是分解得到的小波系数，是阈值，是处理后的小波系数。

4. 重构信号：使用阈值处理后的小波系数重构信号，这样得到的信号中噪声就会被减少。

二、Python代码实现

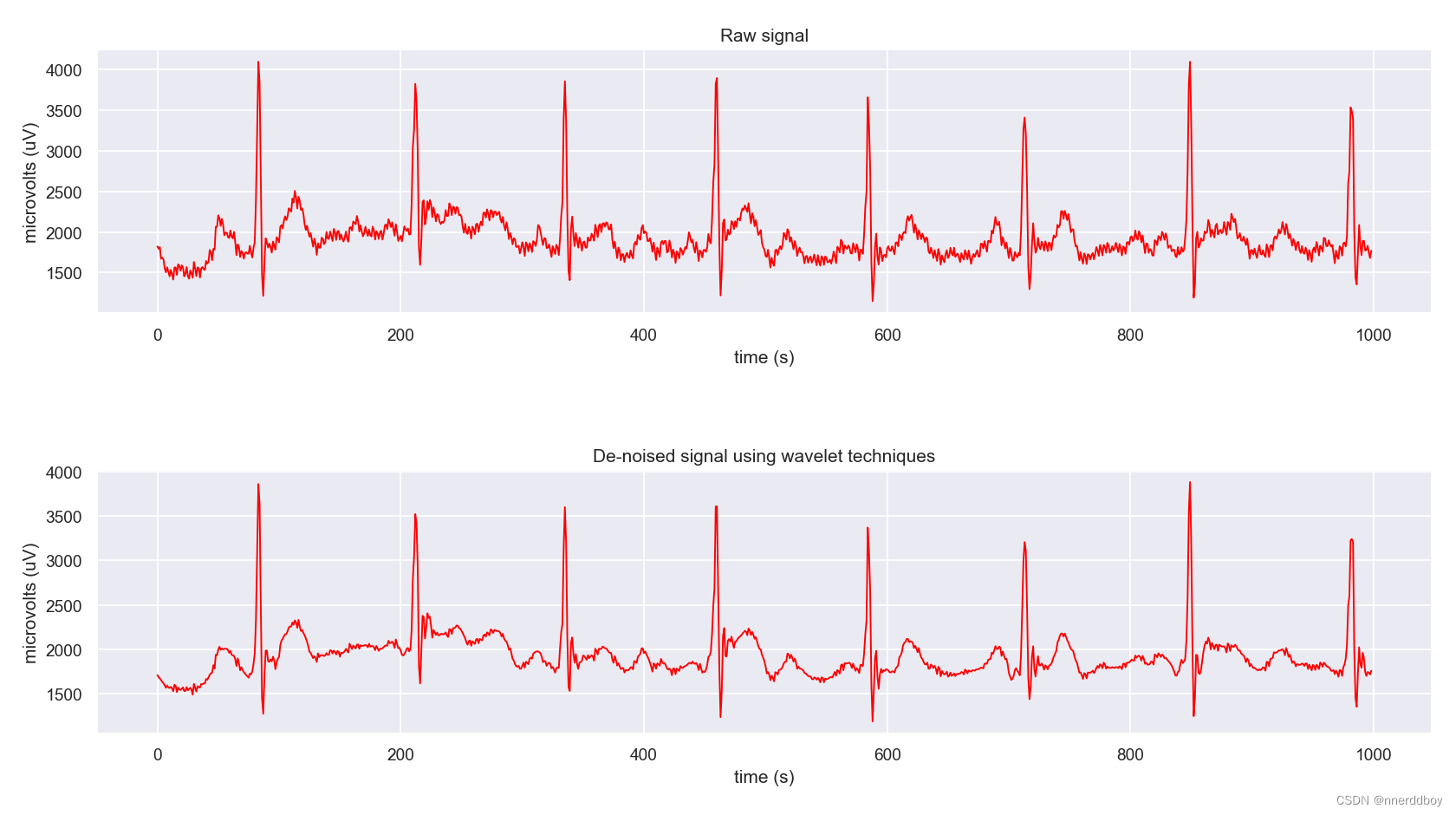
import matplotlib.pyplot as plt import pywt import seaborn as sns sns.set(context='notebook', style='darkgrid', palette='deep', font='sans-serif', font_scale=1, color_codes=False, rc=None) plt.rcParams['axes.unicode_minus'] = False # 防止坐标为负时出现乱码 ecg = [......] # 改成自己的数据 index = [] data = [] for i in range(len(ecg) - 1): X = float(i) Y = float(ecg[i]) index.append(X) data.append(Y) # Create wavelet object and define parameters w = pywt.Wavelet('db4') # 选用Daubechies4小波 maxlev = pywt.dwt_max_level(len(data), w.dec_len) print("maximum level is " + str(maxlev)) # threshold = 0.04 # Threshold for filtering threshold = 0.08 # Decompose into wavelet components, to the level selected: coeffs = pywt.wavedec(data, 'db4', level=maxlev) # 将信号进行小波分解 plt.figure() for i in range(1, len(coeffs)): coeffs[i] = pywt.threshold(coeffs[i], threshold * max(coeffs[i])) # 将噪声滤波 datarec = pywt.waverec(coeffs, 'db4') # 将信号进行小波重构 mintime = 0 maxtime = mintime + len(data) + 1 # plt.xkcd() # 胆小勿入 # plt.figure() plt.subplot(2, 1, 1) plt.plot(index[mintime:maxtime], data[mintime:maxtime], linewidth=1.1, color='r') plt.xlabel('time (s)') plt.ylabel('microvolts (uV)') plt.title("Raw signal") plt.subplot(2, 1, 2) plt.plot(index[mintime:maxtime], datarec[mintime:maxtime - 1], linewidth=1.1, color='r') plt.xlabel('time (s)') plt.ylabel('microvolts (uV)') plt.title("De-noised signal using wavelet techniques") plt.tight_layout() plt.show()

三、结果展示