大家好,欢迎来到IT知识分享网。
同一评价者无相同等级评定时,计算公式:
W = S 1 12 K 2 ( N 3 − N ) W = \frac{S}{\frac{\mathrm{1}}{\mathrm{12}}K^2(N^3-N)} W=121K2(N3−N)S
- N-被评的
对象数; - K-
评分者人数或评分所依据的标准数; - S-每个被评对象所评等级之和Ri 与所有这些和的平均数的离差平方和
S = ∑ i = 1 n ( R i − R i ˉ ) 2 = ∑ i = 1 n R i 2 − 1 n ( ∑ i = 1 n R i ) 2 S = \displaystyle\sum_{i=1}^{n}(R_i-\bar{R_i})^2 = \displaystyle\sum_{i=1}^{n}R_i^2-\frac{\mathrm{1}}{\mathrm{n}}(\displaystyle\sum_{i=1}^{n}{R_i})^2 S=i=1∑n(Ri−Riˉ)2=i=1∑nRi2−n1(i=1∑nRi)2
当评分者意见完全一致时,S取得最大值,和谐系数是实际求得的S与其最大可能取值的比值,故0≤W≤1。
同一评价者有相同等级评定时,计算公式:
W = S 1 12 [ K 2 ( N 3 − N ) − K ∑ i = 1 K T i ] W = \frac{S}{\frac{\mathrm{1}}{\mathrm{12}}[K^2(N^3-N)-K\textstyle\sum_{i=1}^{K}T_i]} W=121[K2(N3−N)−K∑i=1KTi]S
T u = ∑ i = 1 m i ( n i j 3 − n i j ) T_u = \displaystyle\sum_{i=1}^{m_i}(n^3_{ij}-n_{ij}) Tu=i=1∑mi(nij3−nij)
- mi为第i个评价者的评定结果中
有重复等级的个数。 - nij为第i个评价者的评定结果中
第j个重复等级的相同等级数。 - 对于评定结果无相同等级的评价者,Ti=0,因此只须对评定结果有相同等级的评价者计算Ti。
例子1:同一评价者无相同等级评定时
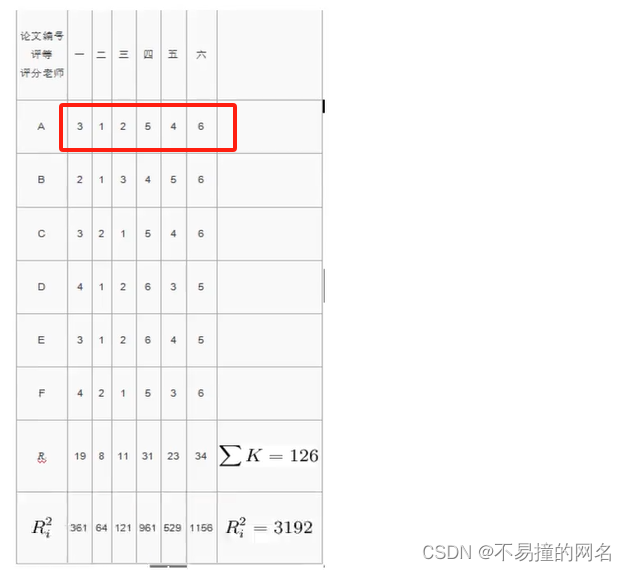
某校开展学生小论文比赛,请6位教师对入选的6篇论文评定得奖等级,结果如下表所示,试计算6位教师评定结果的kandal和谐系数。
由于每个评分老师对6篇论文的评定都无相同的等级:
例子1:同一评价者有相同等级评定时
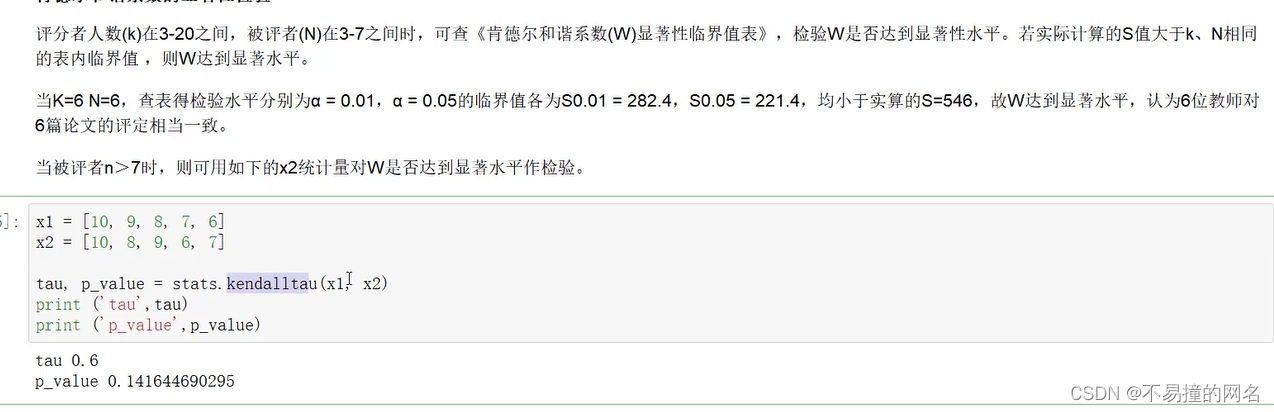
肯德尔和谐系数的显著性检验
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/130391.html