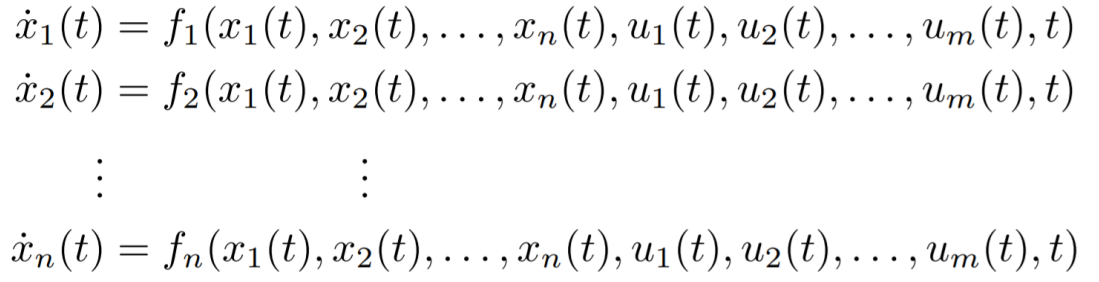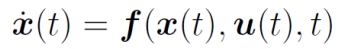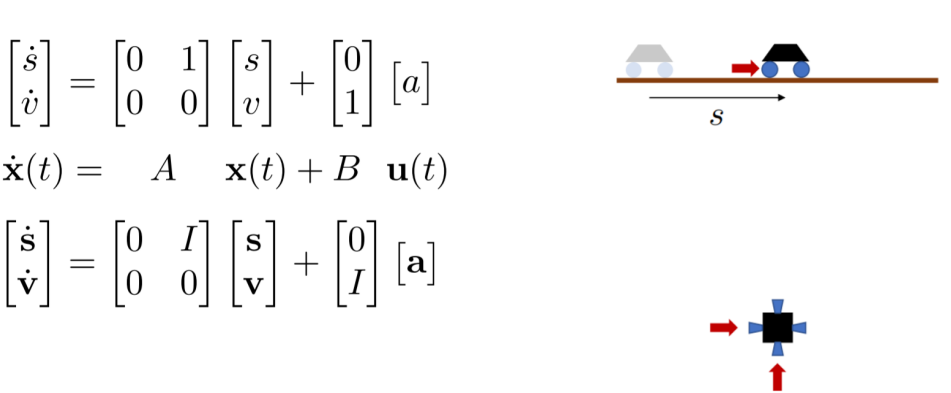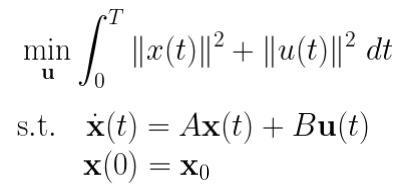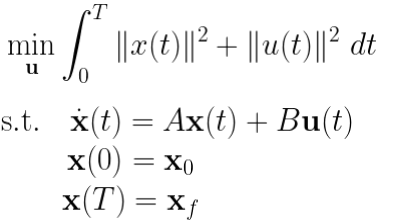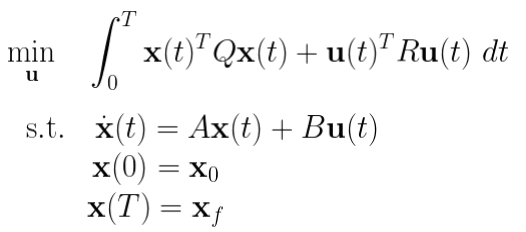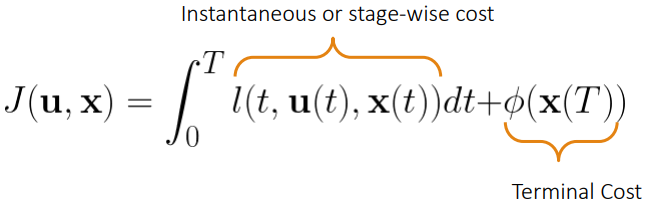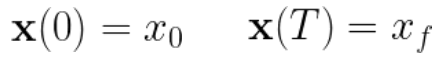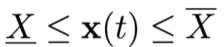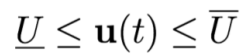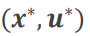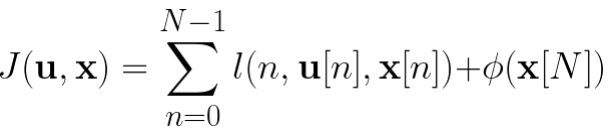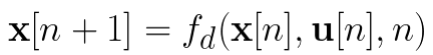最优控制简单理解与控制构架

大家好，欢迎来到IT知识分享网。

概念

最优控制是指在给定的约束条件下，寻求一个控制，使给定的系统性能指标达到极大值(或极小值)。

现代变分理论中最常用的有两种方法。一种是动态规划法，另一种是极小值原理。它们都能够很好的解决控制有闭集约束的变分问题。值得指出的是，动态规划法和极小值原理实质上都属于解析法。

从数学上看，确定最优控制问题可以表述为：在运动方程和允许控制范围的约束下，对以控制函数和运动状态为变量的性能指标函数（ 称为泛函 ） 求取极值（ 极大值或极小值）。

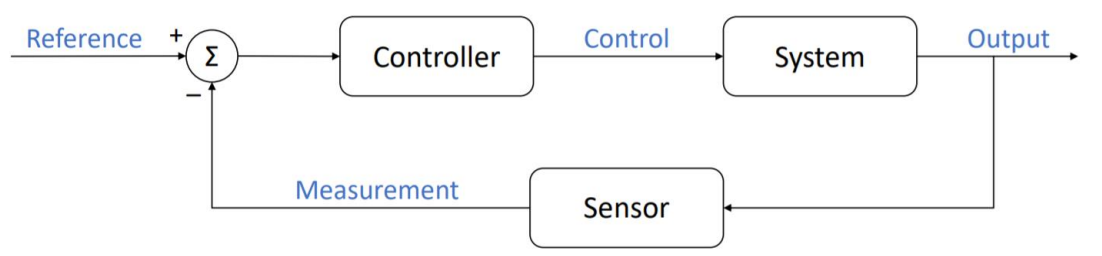
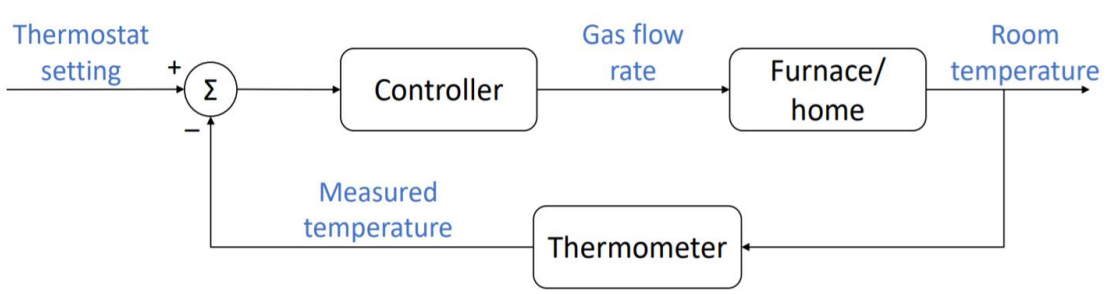
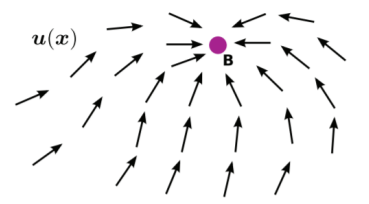
常见的反馈控制的控制目标是：

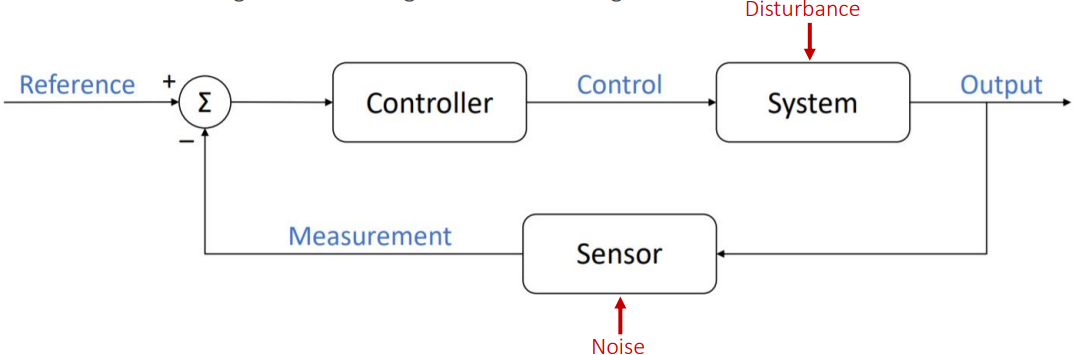
除了上述之外，还需要：

所以，

最优控制问题为：

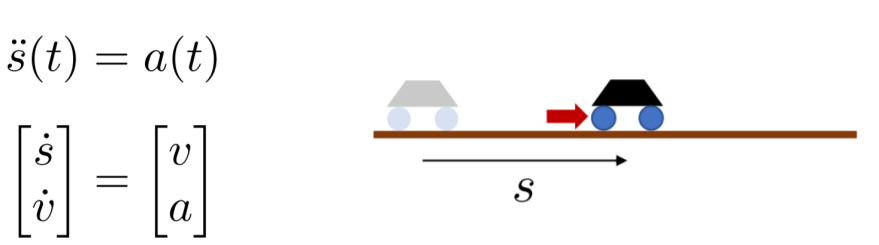
状态空间模型：

那么性能就可以被量化为：

↓

↓

约束：

•初始和最终条件(边界条件):

状态轨迹约束:

•控制限制:

在整个时间区间内满足控制和状态约束的控制历史和状态轨迹被称为可容许的

最小化，

这个就是最优求解的状态与控制量。

离散：

动态：

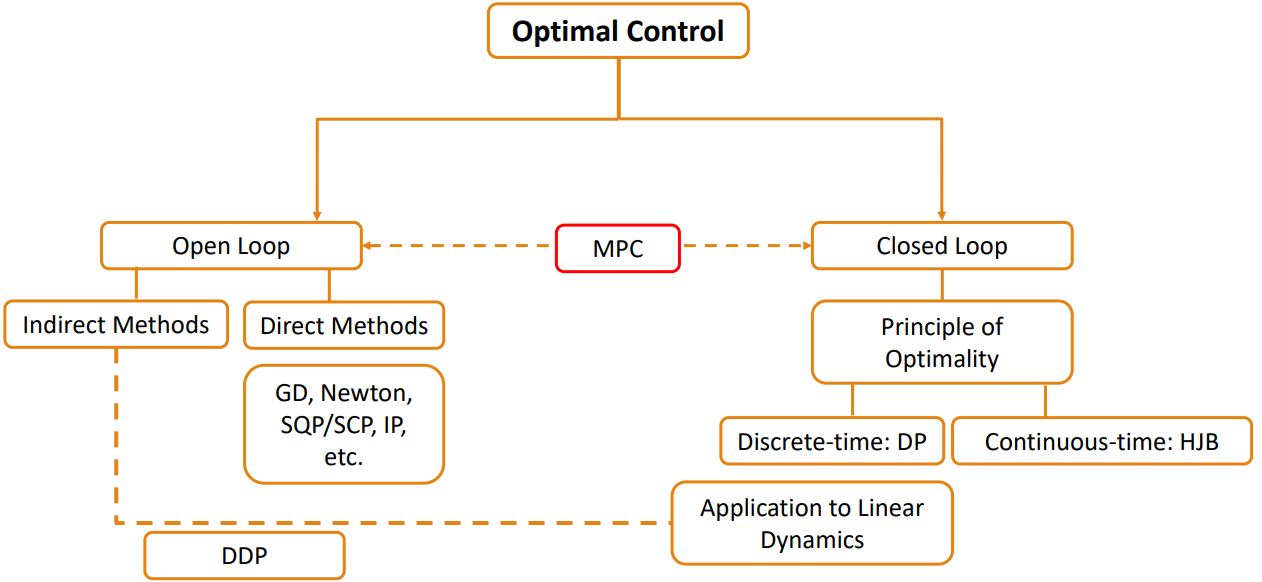
求解方法：

动态规划(最优性原理)
◦最优路径的组合性
◦闭环解决方案:
在任何时候都为所有状态找到解决方案

变分学(庞特里亚金最大值/最小值原理)
◦“最优曲线应该是这样的，相邻曲线不会导致更小的成本”→“导数= 0”
◦开环解决方案:
求一个给定初始状态的解

参考书目：

第1章最优控制问题的提出和数学描述

1.1最优控制问题举例

1.2最优控制问题的数学描述

习题1

第2章函数极值的基本理论

2.1向量函数的无条件极值

2.2等式约束下的向量函数极值

2.3不等式约束下的向量函数极值

习题2

第3章最优控制中的变分法

3.1变分法基本原理

3.2无终端约束的最优控制

3.3终端固定约束的最优控制

3.4终端等式约束的最优控制

3.5终端时刻自由的最优控制

3.6内点等式约束的最优控制

3.7离散时间系统最优控制

习题3

第4章极小值原理

4.1定常系统极小值原理

4.2时变系统极小值原理

4.3不等式过程约束下的最优控制

4.4积分过程约束下的最优控制

4.5离散时间系统极小值原理

习题4

第5章动态规划

5.1Bellman最优性原理

5.2离散系统最优控制的动态规划求解

5.3连续系统最优控制的动态规划求解

5.4三种经典方法的比较

习题5

第6章时间最短和燃料最省控制

6.1时间最短控制与BangBang控制原理

6.2线性定常系统时间最短控制

6.3线性定常系统燃料最省控制

6.4时间与燃料综合最优控制

习题6

第7章线性二次型最优调节器设计

7.1最优调节器问题

7.2连续时间系统有限时间最优状态调节器

7.3连续时间系统无限时间最优状态调节器

7.3.1线性时变系统的情形

7.3.2…