算法 : 关节点问题（邻接表，图的遍历）

大家好，欢迎来到IT知识分享网。

系列文章目录

本系列文章以《算法设计与分析》--C++语言描述 为准，对算法问题进行一一收录

前导：问题描述

问题 : 关节点问题

题目描述

对于一个给定的连通图G，采用深度优先搜索的方法，识别出G的所有关节点。

输入

第一行输入结点个数n和边的个数m，下面m行输入各边。

输出

关节点个数

样例输入

8 10 0 3 0 2 2 3 1 2 2 4 1 4 1 6 5 6 5 7 6 7

样例输出 3

一、基本算法介绍

策略：图的遍历，双连通分量

方法：深度优先生成树（DFS），然后判断是否是关节点。

关节点定义：无向图G=（V,E）中，可能存在某个(多个)结点a，删除a后，图G就不再是连通图，则a就是图G的关节点。

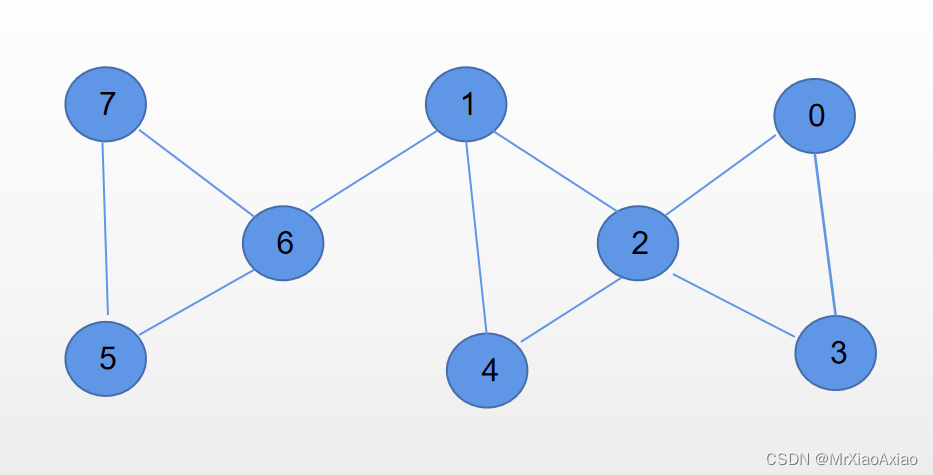
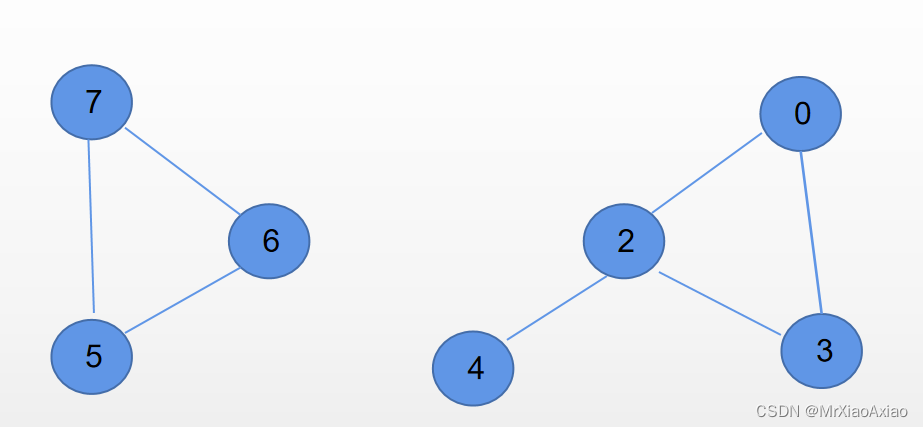
应用场景：例如：通讯网络中的关键结点（如果断开就没办法连接，通讯网络就中断了）

如图：通信网络中的结点

1就是关节点，删除1后图：

二、算法设计

1.算法原理

给定无向连通图G=<V,E>,S=<V,T>是图G的一颗深度优先树，图中的结点a是关节点，当且仅当

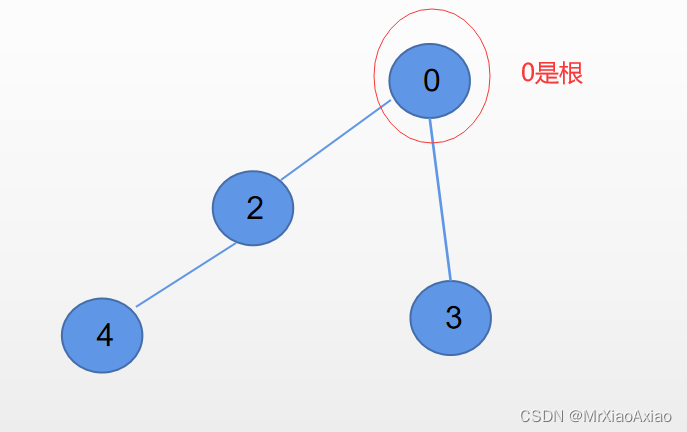
（1）a是根，且a至少有两个孩子

如图：

 

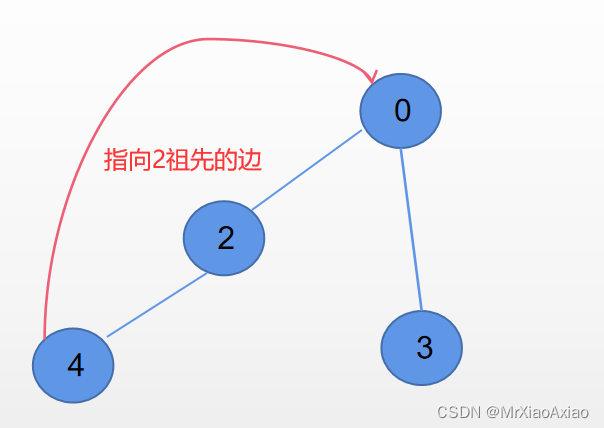
（2）或者a不是根，且a的某子树上没有指向a祖宗的反向边

如图：（此图为非关节点）

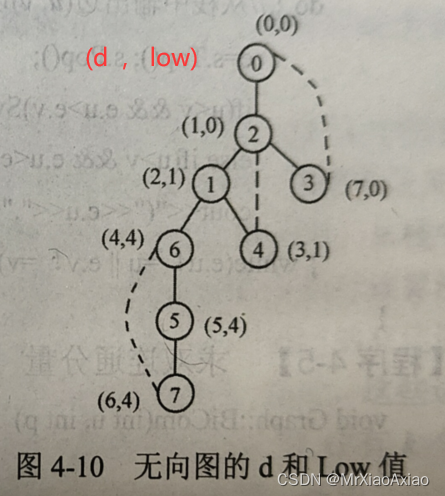
  （3）最低深度优先数：引入low[u]；就是在深度遍历的时候每个结点访问的自己最低的深度。

 

 

 

 

2.程序代码

1.邻接表建立代码如下：

#include <iostream> using namespace std; enum ColorType{White,Gray,Black}; typedef struct ENode { int adjvex; ENode* nexArc; }ENode; int count=0;//根节点的孩子数 int t=0;//时间戳 int d[100],low[100];//d是当前位置，low是能连接到的最早的祖先 int sum=0;//总个数 int pa[100];//parents数组 class Graph { public: Graph( int n, int e); void DFS(int u,int p);//深度有限遍历 void Sum(int n); private: ENode adjlist; int vertexNum; int edgeNum; }; //无向图邻接表存储的构造函数 Graph::Graph(int n, int e){ int i, j, k; ENode* s; vertexNum = n; edgeNum = e; adjlist=new ENode* [vertexNum]; for (i = 0; i < vertexNum; i++) { adjlist[i]= NULL; } for(i=0;i<n;i++)//初始化 d[i]=-1; for(i=0;i<n;i++) pa[i]=-1; for (k = 0; k < edgeNum; k++) { cin >> i >> j; //输入边依附的两个顶点的编号 s = new ENode;//生成一个边表结点s s->adjvex =j; s->nexArc = adjlist[i];//将结点s插入表头 adjlist[i]= s; s = new ENode;//生成一个边表结点s s->adjvex =i; s->nexArc = adjlist[j];//将结点s插入表头 adjlist[j]= s; } }

 

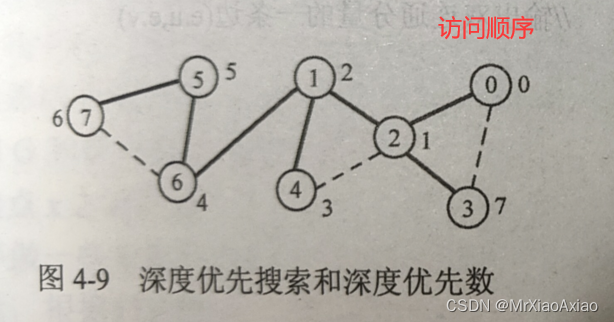
2.深度优先搜索（构造深度优先数）代码如下

void Graph::DFS(int u,int p){ if(p==-1) count++; ENode *w; low[u]=d[u]=t++; for(w=adjlist[u];w;w=w->nexArc){ int v=w->adjvex; if(d[v]==-1){ DFS(v,u); if(low[u]>low[v]) low[u]=low[v]; } else if(v!=p&&low[u]>d[v]) low[u]=d[v]; else if(v==p) pa[u]=v; } }

 

3.计算关节点个数代码如下

void Graph::Sum(int n){ int i,j; for(i=1;i<n;i++){ for(j=1;j<n;j++){ if(pa[j]==i){ if(low[j]>=d[i]){ sum++; break; } } } } }

 

总结

整体代码如下：

 #include <iostream> using namespace std; enum ColorType{White,Gray,Black}; typedef struct ENode { int adjvex; ENode* nexArc; }ENode; int count=0;//根节点的孩子数 int t=0;//时间戳 int d[100],low[100]; int sum=0;//总个数 int pa[100];//parents数组 class Graph { public: Graph( int n, int e); void DFS(int u,int p);//深度有限遍历 void Sum(int n); private: ENode adjlist; int vertexNum; int edgeNum; }; //无向图邻接表存储的构造函数 Graph::Graph(int n, int e){ int i, j, k; ENode* s; vertexNum = n; edgeNum = e; adjlist=new ENode* [vertexNum]; for (i = 0; i < vertexNum; i++) { adjlist[i]= NULL; } for(i=0;i<n;i++)//初始化 d[i]=-1; for(i=0;i<n;i++) pa[i]=-1; for (k = 0; k < edgeNum; k++) { cin >> i >> j; //输入边依附的两个顶点的编号 s = new ENode;//生成一个边表结点s s->adjvex =j; s->nexArc = adjlist[i];//将结点s插入表头 adjlist[i]= s; s = new ENode;//生成一个边表结点s s->adjvex =i; s->nexArc = adjlist[j];//将结点s插入表头 adjlist[j]= s; } } void Graph::DFS(int u,int p){ if(p==-1) count++; ENode *w; low[u]=d[u]=t++; for(w=adjlist[u];w;w=w->nexArc){ int v=w->adjvex; if(d[v]==-1){ DFS(v,u); if(low[u]>low[v]) low[u]=low[v]; } else if(v!=p&&low[u]>d[v]) low[u]=d[v]; else if(v==p) pa[u]=v; } } void Graph::Sum(int n){ int i,j; for(i=1;i<n;i++){ for(j=1;j<n;j++){ if(pa[j]==i){ if(low[j]>=d[i]){ sum++; break; } } } } } int main() { int m,e; cin>>m>>e; Graph graph(m,e); graph.DFS(0,-1);//深度优先搜索 if(count>=2)//判断根节点是不是关节点 sum++; graph.Sum(m); cout<<sum<<endl; return 0; }