大家好,欢迎来到IT知识分享网。
1 坐标系
捷联惯导涉及到多种坐标系。
1.1 坐标系定义
- 惯性坐标系(i):以地球质心为原点, z i z_i zi指向地球自转轴, x i x_i xi轴位于赤道面内,指向空间任意点; y i y_i yi轴构成右手坐标系。该坐标系不随地球自转而转动,但由于地球绕太阳公转以及太阳系绕银河系公转,因此该系不是绝对惯性系,然而这种影响十分微弱,低于惯导的噪声水平,可以忽略不计。
- 地心地固系(e系):与大地测量中的ECEF系一致。
- 当地水平坐标系(L系):原点位于载体质心, x L x_L xL轴沿参考椭球卯酉圈指向东E, y L y_L yL轴沿参考椭球子午线指向北N, z L z_L zL轴沿参考椭球法线指向天U,从而形成ENU坐标系。
- 导航坐标系(n系):运动物体在导航坐标系内进行位置,速度,姿态确定,可选取e系或者L系作为导航系。在L系下导航,物理意义明确,便于理论分析和误差规律探寻,利于内部控制,但动态模型复杂,且不能直接与GNSS等大地测量手段相结合。
- 载体坐标系(b系):捷联惯导硬件内部定义了坐标系,其原点一般位于硬件中心,而惯性元件安装在三个正交方向上行成XYZ轴。将捷联惯导安装在载体上后,惯导硬件的坐标系就成为了载体的坐标系,二者固联在一起。一般Z轴朝上,Y轴朝前进方向,X轴沿前进方向朝右。
- 平台坐标系(p系):在平台式惯导中,惯导通过自身调节,始终维持为一个水平指北平台,这个就是p系,但由于各种误差的影响p系与真实L系并不重合,两者存在一个失准角 ϕ \phi ϕ。在捷联惯导中,这种平台由计算平台所取代,计算平台由b系转向n的姿态矩阵 R b n R_{b}^{n} Rbn来维持,由于解算误差的存在,所计算得到的是存在失准角的姿态矩阵 R b p R_{b}^{p} Rbp, R b p R_{b}^{p} Rbp与 R b n R_{b}^{n} Rbn存在一个失准角 ϕ \phi ϕ。
- 计算机坐标系(c系):L系是由实际经纬度确定的当地坐标系,而惯导自身可以解算出带有误差经纬度 λ c \lambda_{c} λc和 φ c \varphi_{c} φc,由 λ c \lambda_{c} λc和 φ c \varphi_{c} φc确定的当地坐标系称为计算机坐标系。c系实质是模型简化过程中衍生出来的一个坐标系,并没有具体的物理解释,在后续 ψ \psi ψ角误差模型时会详细说明。
1.2 坐标系转换
1.2.1 地心地固系转导航系
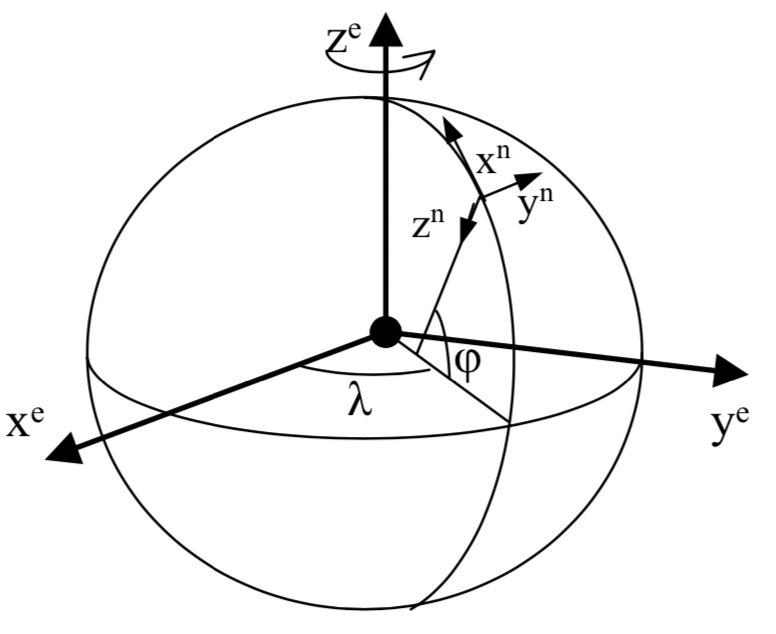
图1 地心地固坐标系与导航坐标系(NEU)
绕z轴旋转 90 + λ 90+\lambda 90+λ: [ c o s ( 90 + λ ) − s i n ( 90 + λ ) 0 s i n ( 90 + λ ) c o s ( 90 + λ ) 0 0 0 1 ] = [ − s i n λ − c o s λ 0 c o s λ − s i n λ 0 0 0 1 ] \begin{bmatrix} cos(90+\lambda) & -sin(90+\lambda) & 0 \\ sin(90+\lambda) & cos(90+\lambda) & 0 \\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} -sin\lambda & -cos\lambda & 0 \\ cos\lambda & -sin\lambda & 0 \\ 0 & 0 & 1 \end{bmatrix}
cos(90+λ)sin(90+λ)0−sin(90+λ)cos(90+λ)0001
=
−sinλcosλ0−cosλ−sinλ0001
绕x轴旋转 90 − φ 90-\varphi 90−φ: [ 1 0 0 0 c o s ( 90 − φ ) − s i n ( 90 − φ ) 0 s i n ( 90 − φ ) c o s ( 90 − φ ) ] = [ 1 0 0 0 s i n φ − c o s φ 0 c o s φ s i n φ ] \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(90-\varphi) & -sin(90-\varphi) \\ 0 & sin(90-\varphi) & cos(90-\varphi) \\ \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & sin\varphi & -cos\varphi \\ 0 & cos\varphi & sin\varphi \\ \end{bmatrix}
1000cos(90−φ)sin(90−φ)0−sin(90−φ)cos(90−φ)
=
1000sinφcosφ0−cosφsinφ
C n e = [ − s i n λ − c o s λ 0 c o s λ − s i n λ 0 0 0 1 ] [ 1 0 0 0 s i n φ − c o s φ 0 c o s φ s i n φ ] = [ − s i n λ − c o s λ s i n φ c o s λ c o s φ c o s λ − s i n λ s i n φ s i n λ c o s φ 0 c o s φ s i n φ ] C_n^e =\begin{bmatrix} -sin\lambda & -cos\lambda & 0 \\ cos\lambda & -sin\lambda & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & sin\varphi & -cos\varphi \\ 0 & cos\varphi & sin\varphi \\ \end{bmatrix}=\begin{bmatrix} -sin\lambda & -cos\lambda sin\varphi & cos\lambda cos\varphi \\ cos\lambda & -sin\lambda sin\varphi & sin\lambda cos\varphi\\ 0 & cos\varphi & sin\varphi \\ \end{bmatrix} Cne=
−sinλcosλ0−cosλ−sinλ0001
1000sinφcosφ0−cosφsinφ
=
−sinλcosλ0−cosλsinφ−sinλsinφcosφcosλcosφsinλcosφsinφ
1.2.2 载体坐标系转导航坐标系
导航坐标系中翻滚角、俯仰角、偏航角的定义方式各种各样,下面给定一种常用的导航坐标系各角度的定义方式:1. 偏航角 ψ \psi ψ,顺时针旋转为正;2. 俯仰角 θ \theta θ,逆时针方向为正;3. 翻滚角 γ \gamma γ,顺时针方向为正。
C b n = [ c o s ψ − s i n ψ 0 s i n ψ c o s ψ 0 0 0 1 ] [ 1 0 0 0 c o s γ − s i n γ 0 s i n γ c o s γ ] [ c o s θ 0 − s i n θ 0 1 0 s i n θ 0 c o s θ ] = [ c o s ψ c o s θ + s i n ψ s i n γ s i n θ s i n ψ c o s γ c o s ψ s i n θ − s i n ψ s i n γ c o s θ s i n ψ c o s θ − s i n γ c o s ψ s i n θ c o s ψ c o s γ − s i n ψ s i n θ − s i n γ c o s ψ c o s θ − c o s γ s i n θ s i n γ c o s γ c o s θ ] \begin{aligned} C_b^n =\begin{bmatrix} cos\psi & -sin\psi & 0 \\ sin\psi & cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\gamma & -sin\gamma \\ 0 & sin\gamma & cos\gamma \\ \end{bmatrix}\begin{bmatrix} cos\theta & 0 & -sin\theta \\ 0 & 1 & 0 \\ sin\theta & 0 & cos\theta \\ \end{bmatrix}\\=\begin{bmatrix} cos\psi cos\theta + sin\psi sin\gamma sin\theta& sin\psi cos\gamma & cos\psi sin\theta -sin\psi sin\gamma cos\theta\\ sin\psi cos\theta – sin\gamma cos\psi sin\theta & cos\psi cos\gamma & -sin\psi sin\theta – sin\gamma cos\psi cos\theta\\ -cos\gamma sin\theta & sin\gamma & cos\gamma cos\theta \\ \end{bmatrix} \end{aligned} Cbn=
cosψsinψ0−sinψcosψ0001
1000cosγsinγ0−sinγcosγ
cosθ0sinθ010−sinθ0cosθ
=
cosψcosθ+sinψsinγsinθsinψcosθ−sinγcosψsinθ−cosγsinθsinψcosγcosψcosγsinγcosψsinθ−sinψsinγcosθ−sinψsinθ−sinγcosψcosθcosγcosθ
2 对准
2.1 静态水平对准:低阶IMU
3 IMU误差补偿
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/131295.html

