opencv基础篇 ——（十五）多边形与凸边型

大家好，欢迎来到IT知识分享网。

概念

多边形（Polygon）
定义： 多边形是一个平面内的闭合图形，由一系列连续的直线段连接而成，首尾相接，且不相交。

特点：

• 可能具有任意数量的顶点（大于等于3个）。
• 各个顶点之间的连接线段称为边。
• 多边形的内部区域称为内部，外部区域称为外部。
• 可以是凸多边形，也可以是凹多边形。

特点：

• 所有内角均小于180度。
• 任意两个点在多边形内的连线都位于多边形内或在多边形边界上。
• 凸多边形的外形呈现凸出的形状，没有凹进去的部分。

示例： 正方形、正五边形等。

区别与联系：

• 所有凸多边形都是多边形，但并非所有多边形都是凸多边形。
• 凸多边形的内部不存在凹陷，而一般的多边形可能存在凹陷。
• 在图像处理中，凸多边形通常更容易处理和计算，因为它们的几何特性更简单，可以更方便地进行边界检测、碰撞检测等操作。
• 在图像处理和计算机视觉领域，常常会使用凸多边形来简化复杂的多边形，以便于进行各种算法和分析。例如，可以使用凸包算法将复杂的多边形转化为凸多边形，以简化形状描述。

isContourConvex

        用于检测轮廓是否为凸形的函数。

函数定义

bool cv::isContourConvex(const std::vector<Point>& contour)

参数

• contour: 输入轮廓，通常是一个 std::vector<cv::Point> 类型的容器，包含了组成轮廓的点的集合。每个 Point 对象代表图像中的一个像素坐标。

返回值

• 如果输入的轮廓是凸的，函数返回 true；否则返回 false。

函数工作原理

• 函数通过执行一种快速的凸包测试来判断轮廓。它尝试找到一个点集的最小凸包，如果这个凸包恰好包含所有的轮廓点，那么轮廓就被认为是凸的。
• 凸包是包围一个形状的最小凸多边形，对于凸轮廓，凸包就是轮廓本身。对于凹轮廓，凸包会超出轮廓的某些部分。

示例用法

// 假设已从图像中找到轮廓 std::vector<std::vector<cv::Point>> contours; cv::findContours(image, contours, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_SIMPLE); for (const auto& contour : contours) { if (cv::isContourConvex(contour)) { // 轮廓是凸的，执行相应的操作 } else { // 轮廓是凹的，执行相应的操作 } }

注意事项

• 轮廓必须是封闭的，也就是说，它的首尾点必须相连。
• 函数对输入轮廓的质量有一定要求，如果轮廓数据不准确或有噪声，可能会影响结果。
• 函数不适用于非连通的轮廓部分，它只能处理单个轮廓。

convexityDefects   

        用于检测和计算给定轮廓的凸包缺陷，即凸形物体上的凹陷或洞。下面是该函数的详细说明：

函数定义

void cv::convexityDefects( InputArray contour, InputArray convexHull, OutputArray convexityDefects )

参数

1. contour: 输入轮廓，通常是一个 std::vector<cv::Point> 或 Mat 类型的数据结构，包含了构成轮廓的点的集合。
2. convexHull: 输入轮廓的凸包，同样是一个 std::vector<cv::Point> 或 Mat 类型的数据结构。这个参数通常可以通过调用 cv::convexHull 函数获得。
3. convexityDefects: 输出的 OutputArray，它将存储每个凸包缺陷的信息，每个缺陷由一个 cv::Vec4i 结构表示。

返回值

函数没有直接的返回值，而是将结果写入到 convexityDefects 输出数组中。

函数工作原理

• 首先，cv::convexHull 函数用于计算输入轮廓的凸包。
• 然后，cv::convexityDefects 检查轮廓上的每个点是否在其凸包内。如果不在，它会确定一个缺陷，这个缺陷由三个关键点定义：
  • 开始点（start_index）：缺陷开始的地方，即从凸包到凹陷内部的最近点。
  • 末尾点（end_index）：缺陷结束的地方，回到凸包上的点。
  • 远点（depth）：从开始点到凹陷最深处的距离，存储在 Vec4i 的第四个元素中，以轮廓点的索引表示距离。

结果表示

每个 cv::Vec4i 结构包含以下四个整数：

• 开始点在 contour 中的索引。
• 末尾点在 contour 中的索引。
• 远点在 contour 中的索引。
• 缺陷的深度（负值，表示距离的绝对值）。

示例用法

// 假设已从图像中找到轮廓 std::vector<std::vector<cv::Point>> contours; cv::findContours(image, contours, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_SIMPLE); // 计算并存储每个轮廓的凸包缺陷 std::vector<std::vector<cv::Vec4i>> defects; for (size_t i = 0; i < contours.size(); ++i) { std::vector<cv::Point> hull; cv::convexHull(contours[i], hull, false); // 不翻转顺序 cv::convexityDefects(contours[i], hull, defects[i]); } // 处理每个轮廓的缺陷 for (const auto& defect : defects) { for (const auto& d : defect) { // 处理每个缺陷 } }

应用场景

• 物体识别：通过检测物体边缘的凹陷来区分不同形状的物体。
• 异常检测：在质量控制中，检测产品表面的凹痕或缺陷。
• 图像分析：理解复杂形状的几何特征。

注意事项

• 凸包缺陷检测仅适用于凸形物体，对于凹形物体，可能需要其他方法来检测特征。

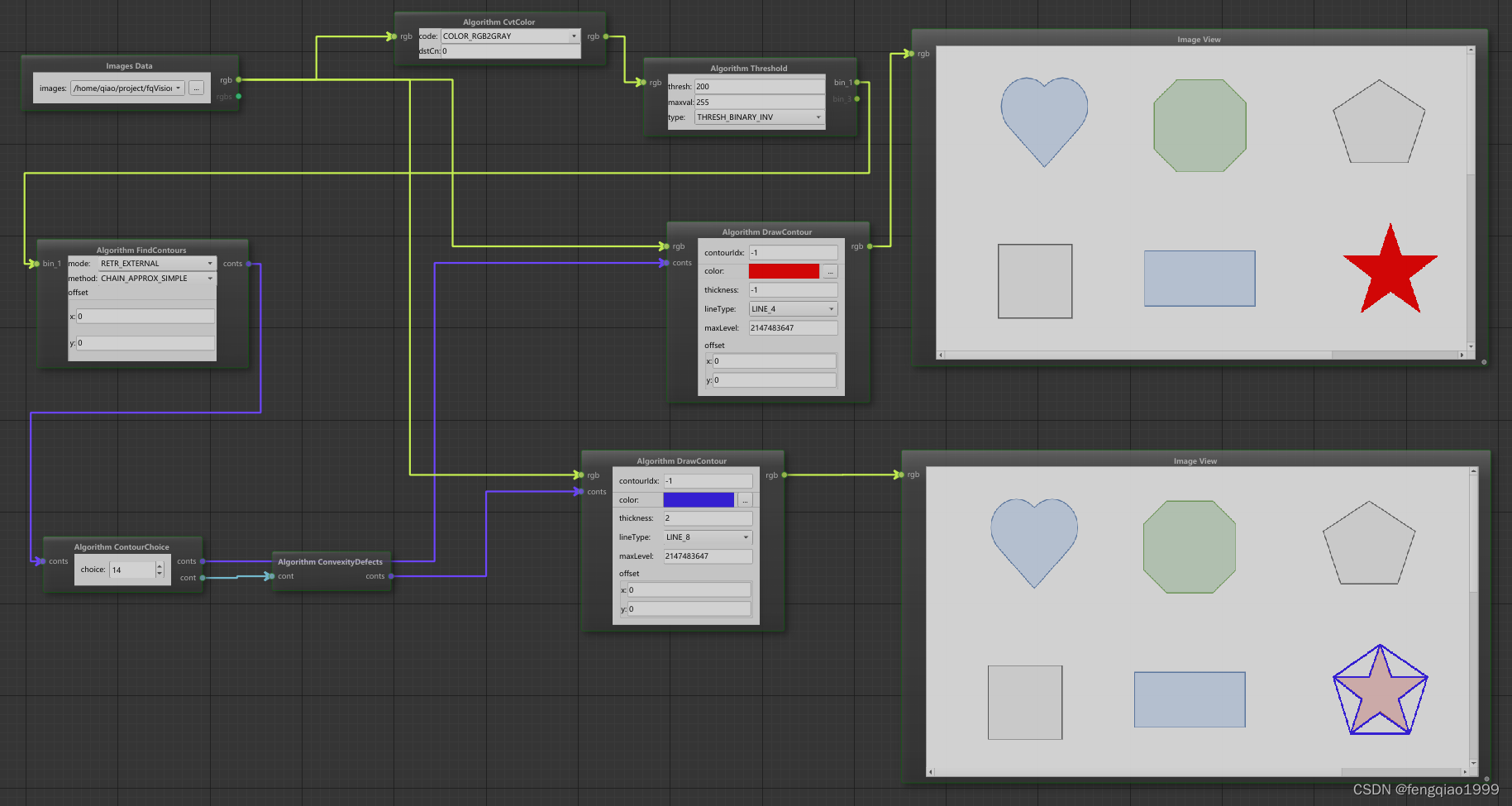
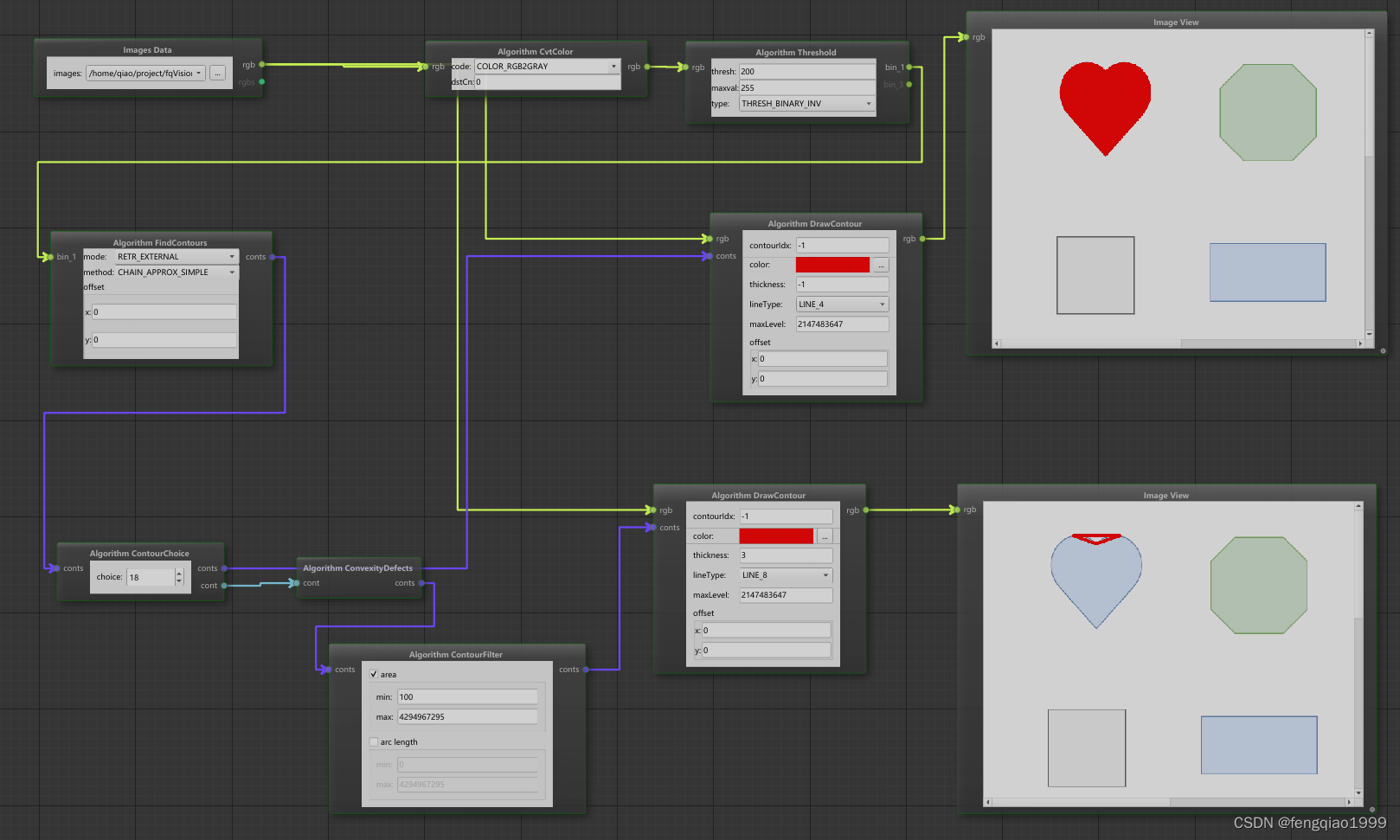
效果展示

检测五角星的缺陷

检测心形缺陷