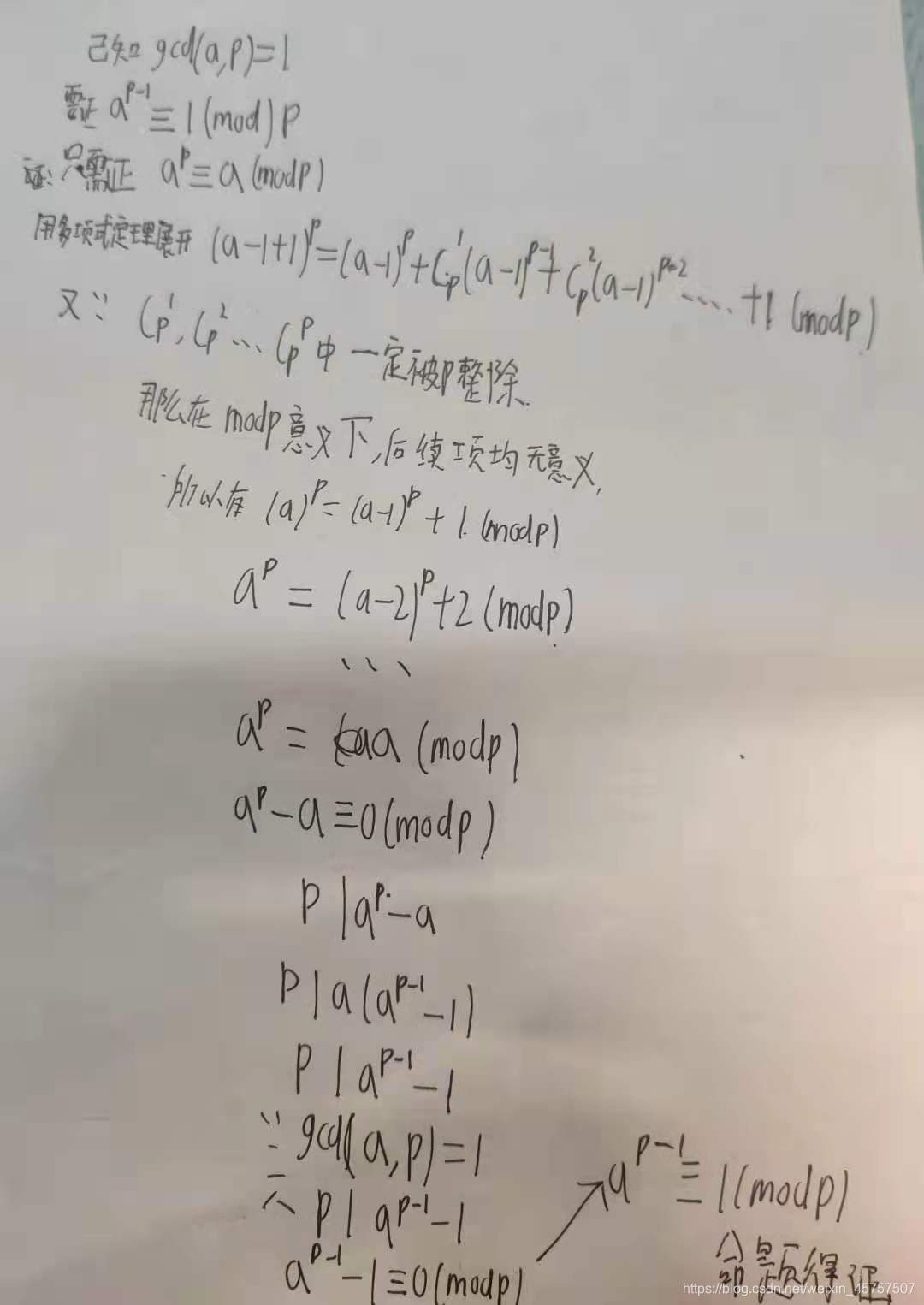数论入门知识

大家好，欢迎来到IT知识分享网。

数论入门

提到数论，可能很多人都感到很头疼，甚至很多时候遇到一些问题，看到成篇的证明都会感到恐惧，而且由于关于ACM方面的数论资料，网上资料都比较驳杂。有时候很容易出现知其然不知其所以然的情况。所以今天给大家介绍一些关于数论入门最基础的知识和算法，内容会尽量从0基础开始，所以内容会尽量详细。不过其中部分证明还是需要一些高中数学基础的。由于内容很多，我整理了一个目录，按顺序讲今天的内容.

目录

一.合数，质数，整除，互质，同余，取模等基础概念。

二.欧几里得算法

三.扩展欧几里得

四.费马小定理

五.欧拉函数

六.欧拉降幂

七.素数筛

八.快速幂

九.逆元的用处和几种简单求法

十.中国剩余定理

一.数论中的基础概念和符号

1.基础概念

合数：合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数

质（素）数：质（素）数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

整除：若整数b除以非零整数a，商为整数，且余数为零， 我们就说b能被a整除（或说a能整除b），b为被除数，a为除数，即a|b（“|”是整除符号），读作“a整除b”或“b能被a整除”。a叫做b的约数（或因数），b叫做a的倍数。整除属于除尽的一种特殊情况。

公约数：公约数，亦称“公因数”。它是指能同时整除几个整数的数 [1] 。如果一个整数同时是几个整数的约数，称这个整数为它们的“公约数”；公约数中最大的称为最大公约数。对任意的若干个正整数，1总是它们的公因数。

互质：互质是公约数只有1的两个整数，叫做互质整数

同余：数论中的重要概念。给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)。对模m同余是整数的一个等价关系

2.常见符号

MOD

同余符号（≡）

sigma（Σ ）

sigma的意思是i取值1（下界）到n（上界）后面的表达式的和，这个公式里的值是1 + 2 + 3 + ⋅ ⋅ ⋅ + ( n − 1 ) + n 1+2+3+···+(n-1)+n1+2+3+⋅⋅⋅+(n−1)+n

求积符号Π

$$\prod _{i=1}^{n}i$$

求积符号，这个公式代表的就是n的阶乘

同余≡

两个整数a，b，若它们除以整数m所得的余数相等，则称a，b对于模m同余

记作 a ≡ b (mod m) 　读作a同余于b模m，或读作a与b关于模m同余。

比如 26 ≡ 14 (mod 12)

μ莫比乌斯函数

代表了莫比乌斯函数。

φ欧拉函数

在数论中代表欧拉函数

定义：小于n的正整数中与n互质的数的数目

|整除符号

整除符号：x|y，表示x整除y，即x是y的因数

gcd（x，y）

代表x和y的最大公约数，也可写作（x，y）

lcm（x，y）

代表x和y的最小公倍数，也可写作[X,Y];

二.欧几里得算法

这种方法把整个证明分为了两部分，第一部分是证明证明gcd(a,b)是b,a%b的一个公约数，第二部分就是证明这个公约数是最大的。 首先我们设gcd(a,b)=d，再令a=k1*d,b=k2*d.我们再设，a=k*b+c（也就是a除以b商k余c），那么c就是余数，也就是a%b. 把上式移项，得到c=a-k*b，然后再把a=k1*d,b=k2*d，这两个式子里的a、b带入式子，得到:c=k1*d-k*k2*d,在提取公因数d，得到c=(k1-k*k2)*d.这样就说明，c，也就是a%b有d这个约数，因为开始我们设b也有d这个约数，所以gcd(a,b)是b，a%b的一个公约数。 知道了这个结论，我们继续来看为什么这个公约数是最大的。 这里我们用到了反证法。我们假设k1-k*k2=q*t,k2=p*t,并且t>1（也就是那两个不互质）。 我们将前面那个式子移项，得到k1=q*t+k*k2,再把这个k1代到最开始的a=k1*d，得到a=（q*t+k*k2）*d，再利用乘法分配律，得到：a=q*t*d+k*k2*d，我们这时发现，k2*d不就是最开始的b吗？，将其带入，得到：a=q*t*d+b*k.这时，我们再把k2=p*t代入开始的b=k2*d,得到b=p*t*d，再把这个式子代到a=q*t*d+b*k.得到了：a=q*t*d+p*t*d*k.提取公因数：a=(q+pk)*t*d。现在，再和b=p*t*d比较，发现他们的最大公因数变成了t*d和开始矛盾，所以假设不成立，反证成功 

证明了这个公式，我们想要算出gcd（a，b）的结果也就很简单了。这两个数的大家都会不断减小，我们只需要递归不断缩小范围低轨道b==0的时候就能算出a和b的最大公约数了，如果gcd（a，b）==1，说明a和b互质。

int gcd(int a, int b) { 
    if (b == 0) return a; return gcd(b, a % b); } int gcd(int a , int b){ 
    return a%b==0? b:gcd(b,a%b); } 

它的时间复杂度是O(log n)；其实很好理解，在递归求gcd的过程中，如果a>b程序会返回gcd（b，a）如果a>b。gcd（a，b）-=gcd（b，a mod b）取模后a的值至少会折半，所以这个过程只会发生logn次。而每次第一种情况后一定会转移到第二种情况，第一种情况的次数不大于第二种情况，所以这个算法的总复杂度是O（log n）级别.

介绍完了最大公约数，不得不提的就是最小公倍数（Least Common Multiple）lcm了。

这里也有一个公式可以直接算，就是gcd（a，b）*lcm（a，b）=a * b

三.扩展欧几里得算法（exgcd）

裴蜀定理

在讲扩展欧几里得之前，我们先介绍一下一个定理，裴蜀定理

裴蜀定理，又称贝祖定理（Bézout’s lemma）。是一个关于最大公约数的定理。

其内容是：设a,b是不全为零的整数，则存在整数x,y , 使得ax+by=gcd(a,b) .

证明就不详细展开了，有兴趣可以上网查一查，其实思想和辗转相除法差别不大。

扩展欧几里得定理

在这个式子里，也就是当b=0是一定成立，假设bx+（a%b）y=gcd（b，a%b）成立，证明ax+by=gcd(a,b)成立 实际上已知bx1+（a%b）y1=gcd（b，a%b）需要证明ax2+by2=gcd（a，b） 我们令a=k*b+c,也就是c是a%b.移项得：c=a-k*b.将这个式子代入到已知式子： b*x1+(a-k*b)*y1=gcd(b,a%b)， 化简可得a*y1+b*(x1-k*y1)=gcd(b,a%b)=gcd(a,b)及当x2=y1 y2=x1-k*y1时满足条件k=a/b 在这个证明过程中，我们只需要通过引用参数的方式，把x和y不断回带。就能得到一组方程的可行解 

关于它的代码

inline int exgcd(int a, int b, int &x, int &y) { 
    if(b == 0){ 
    x = 1, y = 0, return a; } int d = exgcd(b, a % b, x, y); int z = x;x = y, y = z - y * (a / b); return d; } 

通过他我们可以的到方程的一组特解。

这个特解的证明很简单。 方程的特解(x0,y0)任取另一组解 (x,y)，则 ax0+by0=ax+by = gcd (a,b) 。变形得 a (x0−x)=b(y−y0). 设gcd（a，b）=d，方程同时除d，有a1 (x0−x)=b1(y−y0).其中a1=a/d，b1=b/d。 显然a1和b1互质。所以x-x0是b1的整数倍（因为a1不包含b1，所以x-x0一定包含b1）所以可以把x-x0设为kb1在带入式子我们可以得到x-x0=k*b/d。移向就是我们得到的通解。y的证明过程同理可得 

四.费马小定理

这是一种很巧妙的费马小定理证法。但实际上正统的证明方法是引入了完全剩余系和缩剩余系。这些概念在代数系统中式很重要的，不过今天的目的知识给大家见简单介绍数论的基础，暂时不深入展开来讲了。实际上欧拉定理和费马小定理都是拉格朗日定理的一个推论。对于一个有限群，元素的阶一定式群阶数的因子。感兴趣的同学可以在网上查一查相关证明。这里不多赘述

证明完了以后，我们来看看他有什么用

实际上，费马小定理的应用场景还是很广泛的，这里我们只从竞赛的角度说几个它的简单应用。

1.它可以用来判断大质数也就式Miller-Rabin质数判定

3.在后文求解逆元的过程中，我们也会用到费马小定理

五.欧拉定理

到了这里我们其实可以发现，费马小定理就是欧拉定理的在m为素数下的一种特殊情况。通过这个定理在一些特殊情况下求解逆元很好用。并且有一些题目会考察对它的理解，在数论中欧拉定理的应用面非常广泛。是一个非常重要的定理。不过涉及竞赛的一般用的最多就是欧拉降幂公式。我们下面也会提到。这里的证明方法只是帮助大家理解他的本质。如果不理解，在竞赛中，记住欧拉降幂公式和应用就够了。不过理解这些公式的本质在所以写考察思想的题目中还是有所帮助的。

六.欧拉降幂(扩展欧拉定理)

int main() { 
    scanf("%d%d", &a, &m); int flag=0; int phi_m = getphi(m);//欧拉筛晒欧拉函数 cin >> s;//b过大用字符串储存 for(int i = 0; i < s.length(); ++ i) { 
    b = (b * 10 + s[i] - '0'); if(b >= phi[m]) //欧拉降幂 flag = 1, b %= phi[m]; } if(flag) //如果降过幂需要在加phi[m]，质数的欧拉函数为0，不影响结果 b += phi[m]; int ans = qpow(a, b, m);//快速幂取模 printf("%d\n", ans); return 0; } 

七.线性筛

1.Miller-Rabin 素数测试

有时候我们想快速的知道一个数是不是素数，但是数太大这时候我们可以对其进行 Miller-Rabin 素数测试，可以大概率测出其是否为素数。利用了费马小定理和二次探测定理，证明这里不再放出.这里给大家提供一个模板，实际上证明也不复杂，有兴趣可以自己尝试。内容过多不重要的的就不浪费时间了。

bool millerRabbin(int n){ 
    if(n<3)return n==2; int a=n-1,b=0; while(a%2==0)a/=2,++b; // test_time 为测试次数,建议设为不小于 8 的整数以保证正确率,但也不宜过大,否则会影响效率 for(inti=1,j;i<=test_time;++i) { 
    int x=rand()%(n-2)+2,v=quickPow(x,a,n); if(v==1||v==n-1)continue; for(j=0;j<b;++j) { 
    v=(long long)v*v%n; if(v==n-1)break; } if(j>=b)return 0; } return 1; } 

埃氏筛

埃拉托斯特尼筛法，简称埃氏筛，是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。它的实际运用流程其实也很好理解，我们先吧2-n之间的整数写出来，2是最小的素数，把表中2的所有倍数删去，然后现在表中最小的素数是3，由于他没有被比他小的素数整除，他一定是现在最小的素数，我么你继续删去3的所有倍数，以此类推，直到筛到根号n为止。

算法时间复杂度是O(nlog(logn)).在数据范围很大时基本可以看做线性复杂度，足以通过大部分题目。

for(int i=2;i<=N;i++){ 
    if(!vis[i]){ 
    for(int j=2*i;j<=N;j+=i){ 
    vis[j]=1; } } } 

这里是最基础埃氏筛，一般其实够用了，不过在某些情况下，我们还是需要对埃氏筛进行优化，这个优化从三个部分体现出来，我们分别来看他们是如何优化的。

1.首先是第一重优化，其实就是外层i的枚举只需要到根号n即可，这样足够保证n以内的数被筛过。很好理解

2.第二重优化是一个小细节的优化，在第二重循环中，每次增加素数的1倍，但除了2以外素数都是奇数，那么奇数乘以偶数是偶数，偶数情况早已被2筛完，故每次增加2i倍.

3.第三重优化是在第二层循环中把j的起点从i*i开始，因为筛到i的时候已经能保证 i * i范围内没有合数了。

通过这三种常数优化，整个埃氏筛的复杂度几乎和真正的线性筛相差无几，甚至更快一点

for (int i = 0; i <= n; ++i) is_prime[i] = true; is_prime[0] = is_prime[1] = false; for(int i=2;i*i<=N;i++)//将i<=N换成i*i<=N { 
    if(is_prime[i]) { 
    int mul;//2筛过后偶数一定不是素数所以直接加2；  i==2?mul=1:mul=2; for(int j=i*i;j<=N;j=j+i*mul)//将2*i换成i*i is_prime[j]=false; } } 

欧拉筛

埃氏筛已经很接近极限了，但是他还是可以继续优化，在埃氏筛的过程中有的合数会被多次标记，浪费时间，如何解决这个问题呢？这就是是埃氏筛和欧拉筛的最大区别了

欧拉筛思想的核心是要保证的是每个合数只被这个合数最小的质因子筛除，而且只筛一次，没有重复筛除，这里就需要用到这行神秘代码if(i%prime[j]==0) break;。欧拉筛的难点就在于对if (i % prime[j] == 0)这步的理解，当i是prime[j]的整数倍时，记 m = i / prime[j]，那么 i * prime[j+1] 就可以变为 (m * prime[j+1]) * prime[j]，这说明 i * prime[j+1] 是 prime[j] 的整数倍，不需要现在筛出，因为在之后筛除过程中i * prime[j+1] 这个合数一定会被prime[j]筛除，prime[j]之后的所有素数同理，所以break跳出循环。

#include<bits/stdc++.h> using namespace std; const int maxn = 1e6+10; int cnt=0; //记录已知素数数量 vector<int> primes; //存放素数的不定长数组 bool judge[maxn]; //筛除标记 int main() { 
    int i,j; memset(judge,true,sizeof(judge)); judge[0]=false;judge[1]=false;// 0和1都不是素数 for(i=2;i<maxn;i++) { 
    if(judge[i]) { 
    primes.push_back(i); cnt++;//记录素数个数 } for(j=0;j<cnt && i*primes[j]<=maxn;j++) { 
    judge[i*primes[j]]=false; //筛除 if(i%primes[j]==0) //关键代码 break; } } vector<int>::iterator it; for(it=primes.begin();it!=primes.end();it++)//遍历 printf("%d\n",*it); return 0; } 

他能做到真正的线性复杂度，因为他能保证每个数只被筛了一次。

欧拉筛筛欧拉函数

如果只是筛质数，大部分情况埃氏筛就够了，那么欧拉筛还有什么用呢？他当然不知可以用来筛素数，记得在介绍欧拉定理时候就留下了一个问题，如何求欧拉函数。这里我们提供给大家两个方法，大家可以根据题目情况自行选择合适的方法。

1.公式法求欧拉函数

$$\phi (a)=n\ast (1-\frac{1}{p_1})\ast (1-\frac{1}{p_2})\ast \dots \dots \ast (1-\frac{1}{p_n})$$

其中p1到pn是a用唯一分解定理分解出的所有质因数。

这里简单提一下唯一分解定理，他也叫算数基本定理，任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积

。最早的证明也是欧几里得给出的，涉及到欧几里得引理等内容，跟acm关系不大，主要是数论方向的一个重要定理，证明这里就不给出了，有兴趣可以自己查查资料，或者私下来找我交流。

那么这个公式是如何得到的呢？这里需要用到一些积性函数的知识，如果要一起讲的话时间肯定也是不够的，所以暂时也不证了，后续讲积性函数相关内容后很多东西都能联系起来了。这里需要注意的是，在网上有很多资料用这个公式证明了欧拉函数是积性函数，需要注意的是，这种证法其实完全没有意义。因为这个公式是用欧拉函数是积性函数推出来的，要搞清楚因果关系.

inline LL eular(LL x) { 
    LL sum=x,y=x; for (LL i=2;i*i<=y;++i) { 
    if (x%i!=0) continue; sum=sum/i*(i-1); while (x%i==0) x/=i; } if (x>=2) sum=sum/x*(x-1); return sum; } 

2.欧拉筛求欧拉函数

这个过程会涉及积性函数的一些性质。如果要证明推式子，前置知识太多了，所以不给大家证了，直接作为结论给出，相关证明和知识网上也有很多，感兴趣的同学可以自己看一看。这三个性质中的p就是欧拉筛中用来筛当前这个数的最小质因子。

$$\begin{gathered} 如果i是素数，那么\phi (i)=i-1 \\ 如果imodp=0,那么\phi (i\ast p)=p\ast \phi (i) \\ 如果imodp\ne 0，i和p互质那么\phi (i\ast p)=\phi (i)\ast \phi (p)=\phi (i)\ast (p-1) \end{gathered}$$

inline void findphi(void) { 
    phi[1]=1,prm[1]=0; for (LL i=2;i<=n;++i) { 
    if (!v[i]) { 
    prm[++cnt]=i; phi[i]=i-1;//欧拉函数，质数的欧拉函数值为本身-1； } for (LL j=1;j<=cnt && i*prm[j]<=n;++j) { 
    v[i*prm[j]]=1; if (i%prm[j]==0) { 
    phi[i*prm[j]]=phi[i]*prm[j]; break; } if (i%prm[j]!=0) phi[i*prm[j]]=phi[i]*(prm[j]-1); } } return; } 

八.快速幂

可以再O（logn）复杂度内解决问题，其实本质就是把要求的数的幂次看成二进制的数，然后然后分解成二进制的每一位。在进行相乘。

$$a^{11}=a^{2^3}\ast a^{2^1}\ast a^{2^0}$$
分解之后我们只需要知道a^1,a2,a^{4,…。用logn次乘法就能算出a}n。

如果需要取模，就在每一步直接加上取模操作即可

long long pow(long long a,long long b,long long m) { 
    a%=m; long long res=1; while(b>0) { 
    if(b&1)res=res*a%m; a=a*a%m; b>>=1; } return res; } 

九.逆元的应用和几种求法

1.逆元的定义

2.逆元的应用

知道了这些那么我们继续探讨逆元是如何得到的。这里给大家提供4种方法，在不同的情况选选择合适的方法来解决逆元。

3.逆元的4种求法

1.费马小定理求逆元

上面我们也介绍了费马小定理。

如果我们的模数p是质数。我们就可以用费马小定理来求一个数的逆元。

LL pow(LL a, LL b, LL p){ 
   //a的b次方求余p  LL x = 1; while(b){ 
    if(b & 1) x = (x * a) % p; a = (a * a) % p; b >>= 1; } return ret; } LL Fm(LL a, LL p){ 
   //费马求a关于b的逆元  return pow(a, p-2, p); } 

适用情况

2.扩展欧几里得算法求逆元

#include<cstdio> typedef long long LL; void exgcd(LL a,LL b,LL &x,LL &y,LL &d){ 
    if(b==0) d=a,x=1,y=0; else exgcd(b,a%b,x,y,d),t=x,x=y,y=t-a/b*y; } LL inv(LL t, LL p){ 
   //如果不存在，返回-1  LL d, x, y; ex_gcd(t, p, x, y, d); return d == 1 ? (x % p + p) % p : -1; } int main(){ 
    LL a, p; while(~scanf("%lld%lld", &a, &p)){ 
    printf("%lld\n", inv(a, p)); } } 

适用情况

只要存在逆元，就可以用exgcd来求解逆元.复杂度为O（logn），也是我们最常用的一种方法。适用于要求的逆元个数不多的情况。

3.递推求逆元

有了这个式子。我们就可以直接用递推的方式O（n）求出1-n所有数的逆元。

LL inv[mod+5]; void getInv(LL mod) { 
    inv[1]=1; for(int i=2;i<mod;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod; } 

适用情况

时间复杂度O(n)一般用于模数是素数且要多次调用逆元的情况，比如卢卡斯定理等。

递归求逆元

到这里其实也很容易发现了，如果我们只是单独求某个数的逆元。完全可以用递归的方法去做，用的还是上面给出的公式.

LL inv(LL i) { 
    if(i==1)return 1; return (mod-mod/i)*inv(mod%i)%mod; } 

适用情况

复杂度O（n^{1/3）至于它的复杂度证明比较复杂，但是实际情况复杂度可以看做o（logp）p是模数。为什么有两种复杂度呢？这个算法本质上有两种上界。并且大小不定。实际运算复杂度应该会取两种复杂度中低的一种。根据实验。大部分情况，这个算法的复杂度都是logp级别的，也就是说它的复杂度不会超过O（n}1/3).那么他可以保证一定比扩展欧几里得和费马小定理优秀，至于上界为什么是O（n^1/3).有一篇论文给出了比较详细的证明

https://cs.uwaterloo.ca/research/tr/1996/21/cs-96-21.pdf 

cs-96-21.dvi (uwaterloo.ca)

如果模数是质数直接用就行。代码也短。

十.中国剩余定理（CRT)

孙子定理是中国古代求解一次同余式组的方法。是数论中一个重要定理。又称中国余数定理。一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

解决这个问题就要用到中国剩余定理。我们来看一下他的内容是什么

这里我们得到是一组构造出来的特殊接，方程的通解就是x+km如果要求最小非负解。只需要把x对m取模。保证x在0-m-1的范围内即为最小正整数解。

这里的ti其实就是Mi的逆元

那么这个问题写在代码中就只需要求逆元即可。

const ll N = 5e5 + 7; int n, a[N], m[N]; ll exgcd(ll a, ll b, ll &x, ll &y) { 
    if(b == 0){ 
    x = 1; y = 0; return a; } ll d = exgcd(b, a % b, x, y); ll z = x;x = y;y = z - (a / b) * x; return d; } int main() { 
    ll M = 1; scanf("%d", &n); for(int i = 1; i <= n; ++ i) { 
    scanf("%d%d", &m[i], &a[i]); M *= m[i]; } ll res = 0; for(int i = 1; i <= n; ++ i) { 
    ll Mi = M / m[i]; ll ti, y; //exgcd求逆元：解同余方程：ax + my = 1;(ax ≡ 1 mod m) ll d = exgcd(Mi, m[i], ti, y); ti = (ti % m[i] + m[i]) % m[i]; res += a[i] * ti * Mi; } printf("%lld\n", (res % M + M) % M);//可能为负数，所以需要处理一下 return 0; } 

小结

今天讲的内容其实只是数论知识的冰山一角，并且有些地方的证明还需要一些其他知识来辅助。希望大家在学习数论的过程中还是要注重理解证明。这些证明思想会是你学习过程中最大的收获。本文尽可能用简单的语言和基础知识给一些数论基础知识做了铺垫。希望能帮到大家.有的地方latax挂掉了。换成图片了