学不会最短路问题？看这篇就够了

大家好，欢迎来到IT知识分享网。

数据结构入门学习（全是干货）——图论问题之最短路径

1 最短路径问题概述

最短路径问题的定义

• 在一个网络（图）中，求解两个顶点之间所有路径中边的权值之和最小的路径。这条路径称为最短路径。
  • 源点(Source)：第一个顶点
  • 终点(Destination)：最后一个顶点

a点到b点之间路径可达最短的一条线路就是最短路径 或者说是从a点到b点最省钱的路线，这也是一种最短路的问题 ->这种情况下什么是长什么是短？ //区别就在边上的权重(我们赋予了他们什么意义)，比如我们要找最便宜的路径，那么两点之间的那个边的权重就应该定义成票的价格 //我们要找的就是票的价格的和是最小的那条路 假如我们要找的是a站点到b站点最快的那个路径，这时候什么叫快？ //是 经停的站最少的快 还是说 途经时间最短的快。在这里我们选择前者 //这时候边的权重就定义为1，经停站的个数就是每条边加起来的了 

问题分类

1. 单源最短路径问题：
   • 从一个固定源点出发，求其到图中所有其他顶点的最短路径。
   • 适用于无权图和有权图。
2. 多源最短路径问题：
   • 求解任意两顶点之间的最短路径。

1.2 无权图的单源最短路径

• 可以使用广度优先搜索(BFS) 来求解单源最短路径。
  • 按照递增（非递减）顺序，逐步扫描图中的顶点，确定到其他顶点的最短路径。

  

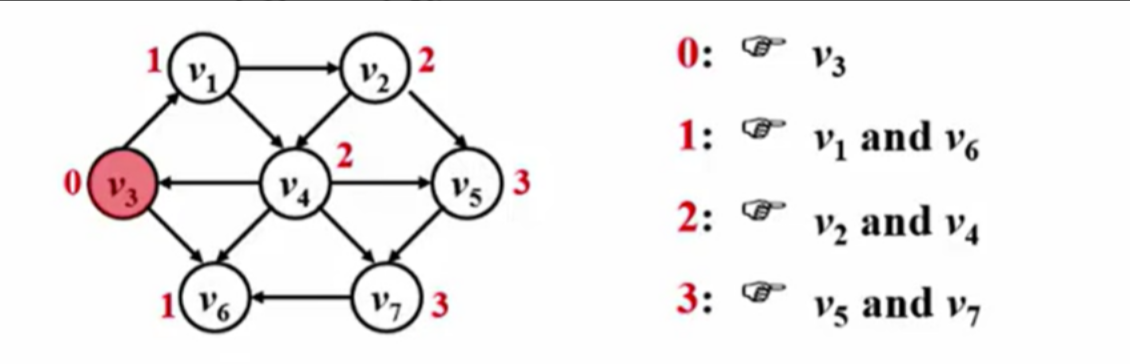
  void Unweighted ( Vertex S )//unweighted是无权的意思 { 
        Enqueue(S,Q); while(!IsEmpty(Q)){ 
        V = Dequeue(Q);//每次弹出来一个顶点，就意味着这个顶点到s的最短路径已经被找到了 for ( V 的每一个邻接点 W ) if( dist[W] == -1 ){ 
       //正常的数都是正数，-1是属于不会被访问过的 dist[W] == dist[V]+1;//这个时候W的最短距离就找到了 path[W] = V//谁是S到W路上必经的顶点呢？那就是他的前一个顶点(V是顶点的编号)。记录下来这个的作用是：顺着path这个数组一个一个往前推，直到推到源点得到一个反向的路径(然后将其压到堆栈里面(堆栈起反序作用，后序先出)，从而得到正确的路径) Enqueue(W,Q); } } } 

  • 时间复杂度：对于包含 (|V|) 个顶点和 (|E|) 条边的图，如果采用邻接表存储，则时间复杂度为 (O(|V| + |E|))。

无权图的单源最短路示例

 void Unweighted ( Vertex S )//unweighted是无权的意思 { 
    Enqueue(S,Q); while(!IsEmpty(Q)){ 
   //这是判断他是不是为空再决定要不要进行下去 V = Dequeue(Q); for ( V 的每一个邻接点 W ) if( dist[W] == -1 ){ 
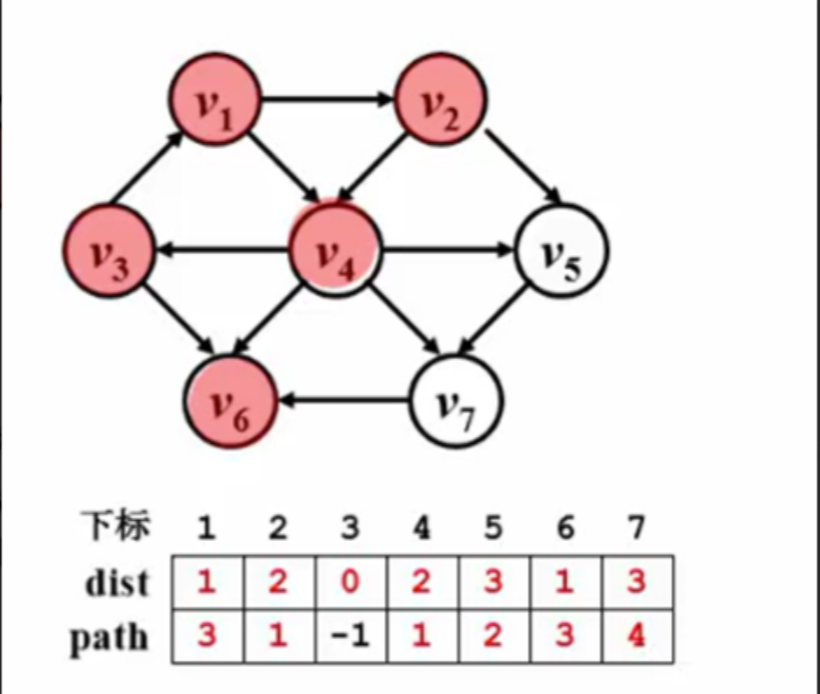
   //正常的数都是正数，-1是属于不会被访问过的 dist[W] == dist[V]+1; path[W] = V Enqueue(W,Q); } } } //dist是点到源点的最短距离 //path是指当前点在那条路径上 //所以所有的信息就都可以从表格中得到 

1.3 有权图的单源最短路径

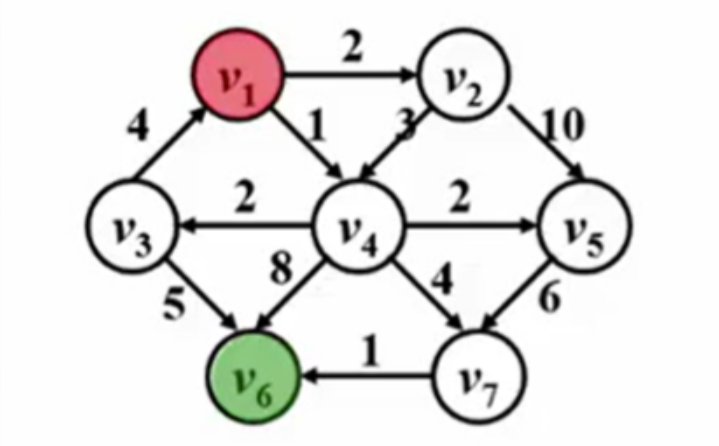
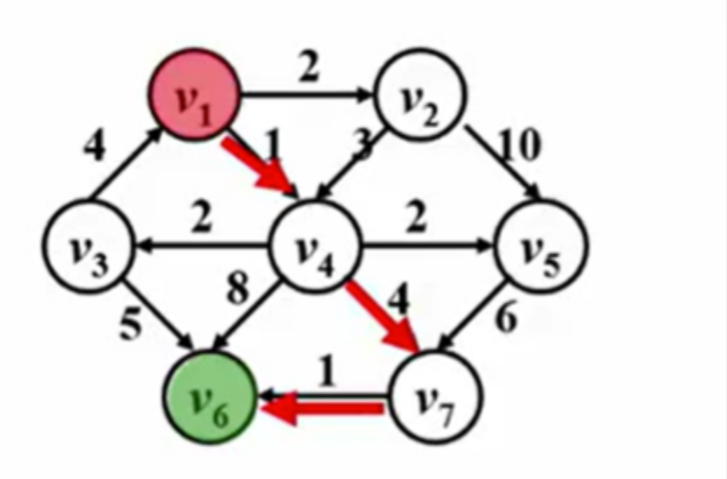
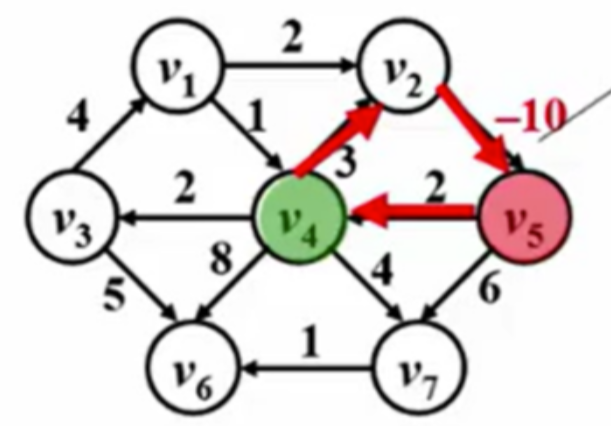
由图得知从红色的位置到绿色的最短路径是哪条？

是这条啦

有权图跟无权图最短路的区别

有权图的最短路不一定是经过顶点数最少的那条路，上图就很好的证实了这点 上图的最短路上的全重合时1加8等于9.但有权图的最短路是1+4+1=6(权重更低) 

如果路径上的权重还有负数的话，是不是最短路又会发生改变，比如这样：

这个图我如果不停的循环，每圈赚5块，那无限转圈不就反而倒赚正无穷(美好的愿望hh)

这种情况叫做有一个负值圈叫做(negative-cost cycle)

1. 图里面要是有这样一种负值圈的话，基本上所有的算法都会挂掉，所有后面不考虑这种情况
2. 算法相通之处：按照递增(非递减)的顺序找出到各个顶点的最短路

Dijkstra算法

• 适用于边权值为非负数的有向图或无向图。
• 基于贪心策略，逐步将顶点加入到集合 (S)，并更新其到其他顶点的最短路径。
  1. 初始化：将源点加入集合 (S)，定义一个距离数组 dist 来记录从源点到每个顶点的最短路径长度。
  2. 选择最小路径：每次从未收录的顶点中选择 dist 最小的顶点加入集合 (S)。
  3. 更新路径：对于新加入集合的顶点，检查是否能通过它更新其他顶点的最短路径。
• 时间复杂度：(O((|V| + |E|) \log |V|)) 取决于实现方式，常用优先队列来优化顶点的选择。
• 算法框架

  void Dijkstra(Vertex s) { 
        while(1){ 
        V = 未收录顶点中dist最小者; collected[V] = true;//收到集合里面 for( V的每个邻接点 W ) if( collected[W] === false ){ 
        if( dist[V]+E<v,w> < dist[W] ){ 
       //this不能随便初始化，因为这个不等式在的原因，我们当描述一个顶点跟s没有直接的路可以通的时候，一定要把它定义成正无穷，这样当我们发现一个更短路径的时候，才可以把这个往更小的地方去更新(假如我们随便把它定义成-1的话，那这个不等式永远都不会成立了) dist[W] = dist[V] + E<v,w>;//<v,w>是下标 path[W] = V; } } } }//Dijkstra算法不能解决有负边的情况，因为这个算法的思路是按照距离从小到大的顺序去收集每一个顶点，如果有一条边是负的，那么对于某一个w来说就有可能说就有了一个dist v 然后他减掉了一个正值，我们就可以得到一个比v还要短的w。然后w之前是排在v的后面的，所以整个算法会乱掉 假如有边的话？要怎么做 Dijkstra算法的时间复杂度：不科学，没有欸。因为在上面的代码中只是一个伪代码演示 在 dist[W] = dist[V] + E<v,w>; 中说的是如果我有一个更短的距离，我要把这个值更新为这个最短的距离。这个更新不一定是一个简单的赋值 方法1：直接扫描所有未收录顶点 -O(|V|)//这个的时间复杂度就是OV //使用方法1这种粗暴的方式的话那后面的赋值语句真的就只是一行了。得出来的整体复杂度就是 T = O(|V|²+|E|)，扫描一遍是V个，一共扫描V遍且扫描的时候涉及边的每个邻接点，也就是每条边又被访问了一遍 //对于稠密图效果好，稠密图是指那些有很多边的(边的条数跟顶点的个数是OV平方数量级的) 方法2：将dist存在最小堆中 -O(log|V|) //每次只要把堆的根节点弹出来，然后调整这个最小堆，每次获得最小距离的这一步操作是一个logv的时间复杂做的算法，比前面OV快多了 //更新dist[W]的值 -O(log|V|)变成稍微复杂的事情，不仅要把值更新，还得把它插回那个最小堆里面去 //总体复杂度：T = O(|V|log|V| + |E|log|V|)，这个堆稀疏图效果好，如果是稠密图的话可以将复杂度写成elogv 稀疏图：e跟V是同一个数量级的，不是V平方数量级的，复杂度就是vlogv 

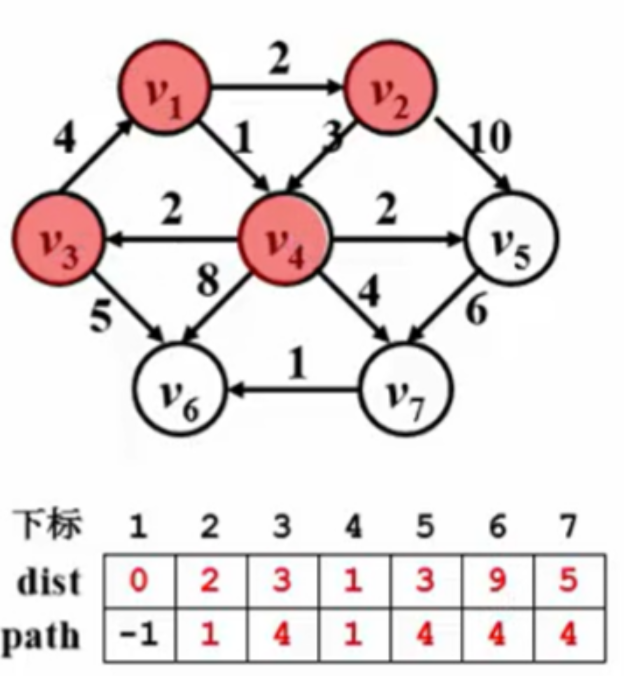
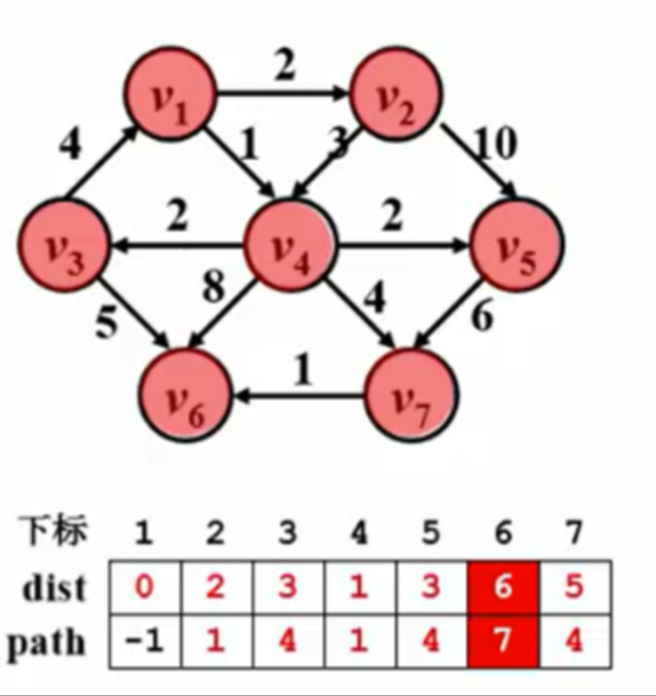
有权图的单源最短路示例

void Dijkstra( Vertex s ) { 
    while(1){ 
    V = 未收录顶点中dist最小者; if( 这样的v不存在 ) break; collected[V] = true; for( V的每个邻接点W ) if( collected[W] == false ) if( dist[V] + E<v,w> < dist[W] ){ 
   //小于正无穷就执行，dist[W]还未经过的点是默认为正无穷 dist[W] = dist[V] + E<v,w>; path[W] = V; } } } 下图中的dist表示源点到目标点之间的权重，path表示当前点的上一个点的下标 

刚开始：

正式进入Dijkstra算法：

进行邻接点排除前：

排除完后：

负权图问题

• 若图中包含负权边，则最短路径算法可能需要特别处理。常见问题是负权环(negative-cost cycle)，在存在负权环的情况下，算法可能会进入死循环，因为可以通过不断绕环来减少路径长度。
  • 对于包含负权边的图，可以使用Bellman-Ford算法，它可以检测负权环并处理负权边的情况。

1.4 多源最短路径算法

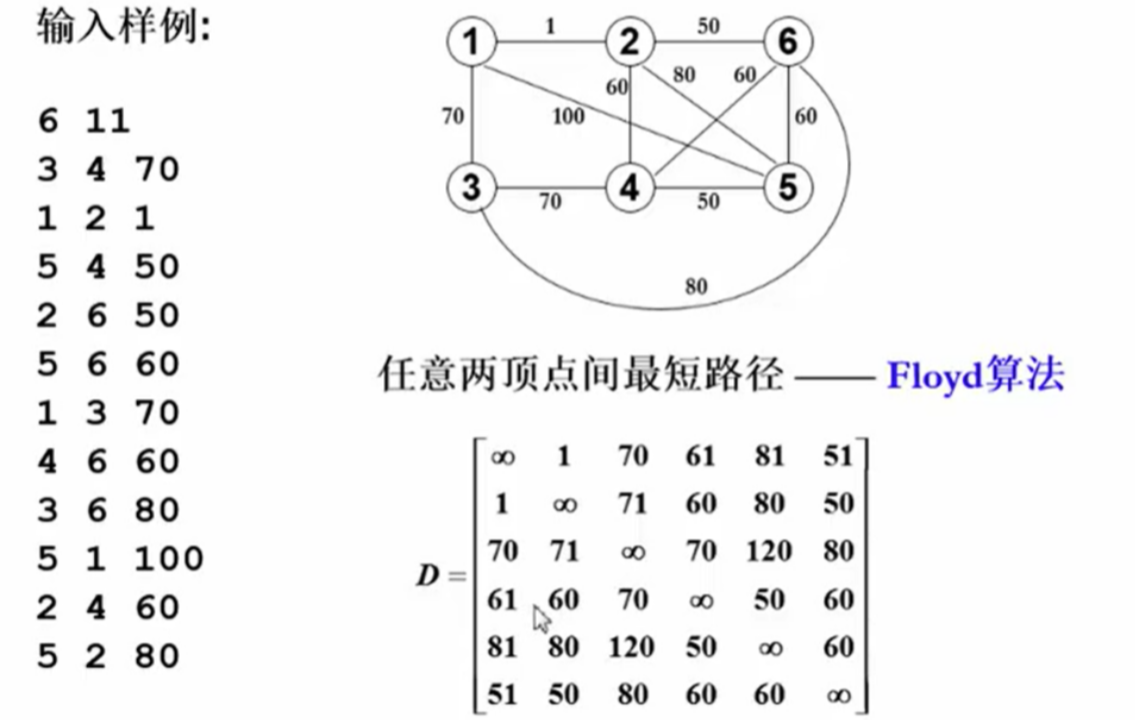
Floyd算法

• Floyd-Warshall算法 用于解决多源最短路径问题，适用于稠密图。
  • 通过逐步考虑每个顶点 (k)，更新其他两顶点 (i) 和 (j) 之间的最短路径。如果经过顶点 (k) 可以得到更短的路径，则更新该路径。
  • 初始时，如果顶点 (i) 和 (j) 之间没有直接边，则定义其距离为正无穷大。
  • 通过不断迭代，最终求得每两个顶点之间的最短路径。

Floyd算法伪代码

bool Floyd(MGraph Graph ,WeightType D[][MaxVertexNum],Vertex path[][MaxVertexNum]) { 
    Vertex i, j, k; // 初始化 for (i = 0; i < Graph->Nv; i++) for (j = 0; j < Graph->Nv; j++) { 
    D[i][j] = Graph->G[i][j]; path[i][j] = -1; } // 核心算法 for (k = 0; k < Graph->Nv; k++) for (i = 0; i < Graph->Nv; i++) for (j = 0; j < Graph->Nv; j++) if (D[i][k] + D[k][j] < D[i][j]) { 
    D[i][j] = D[i][k] + D[k][j]; path[i][j] = k; } return true; // 如果成功计算最短路径，返回 true } 

小白专场：哈利 波特的考试

小白-HP.1 题意理解

样例第一列表示动物的个数(也就是顶点的个数) 第二列表示边的个数 D是最短距离的矩阵，记录从顶点i到顶点j之间的最短距离 Harry究竟应该带哪只动物去的问题的时候，首先检查每一行里面最大的那个数字，最大的那个数字代表着第一个动物变成最大数字的那个动物是最麻烦的，无穷符号指当前的那个动物 要带什么动物去会使我们最难变的动物变成最好变的呢？答案是动物4号，它最难变的咒语是70 

小白-HP.2 程序框架搭建

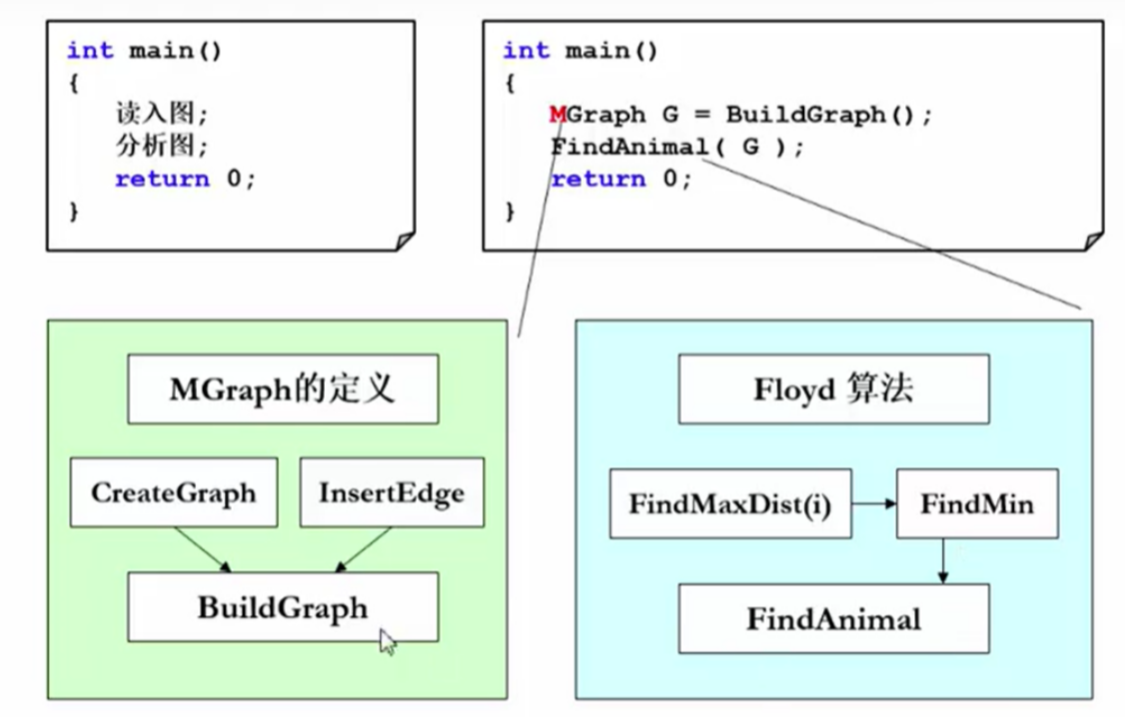
 int main() { 
    读入图; 分析图; return 0; } 

代码实际演示

int main() { 
    //有两种图，一种邻接表的，一种邻接矩阵的。这里选择了邻接矩阵的方法来表示图 Graph G = BuildGraph(); FindAnimal( G ); return 0; } //FindMaxDist(i)是最大距离，对第i个动物去求他所有最短距离里面的最大值，要求的是所有这些最大值里面的最小值 //FindMin是最小距离 

小白-HP.3 选择动物

void FindAnimal(MGraph Graph) { 
    WeightType D[MaxVertexNum][MaxVertexNum],MaxDist,MinDist; Vertex Animal, i; Floyd(Graph , D); //FindMin:从每个动物i的最短距离的最大值中，找到最小值MinDist,以及对应的动物编号Animal MinDist = INFINITY; for( i = 0;i<Graph->Mv;i++){ 
    MaxDist = FindMaxDist(D,i,Graph->Nv);//找到第i个动物它的最大的那个距离赋给MaxDist这个变量 //还有一个特殊情况需要考虑：带一只动物去根本不可能，当图不连通的时候，图有不止一个连通集。该从哪里意识到图不连通了呢？ if(MaxDist == INFINITY){ 
   //返回距离无穷大的话说明有i无法变出的动物 printf("0\n"); return; } if( MinDist > MaxDist ){ 
   //找到最长距离更小的动物 MinDist = MaxDist; Animal = i + 1;//更新距离，记录编号。这里是i+1是因为动物编号从1开始，但是图的循环从0开始，所有需要加一 } } printf("%d %d\n",Animal,MinDist); } 

上述代码中涉及到封装起来的函数

WeightType FindMaxDist(WeightType D[][MaxVertexNum],Vertex i,int N) { 
    WeightType MaxDist; Vertex j; MaxDist = O;//初始化为一个很小的数，比如0 for(j = 0;j < N;j++ )//找出i到其他动物j的最长距离 if( i != j && D[i][j]>MaxDist )//邻接矩阵所有的两个顶点之间的距离全部初始化为正无穷，所以对角元的值永远是正无穷。所以必须要把对角元排除掉跳过去，不排除的话这个无穷大必然会符合这个判断条件从而让MaxDist永远的返回正无穷 MaxDist=[i][j]; return MaxDist; } 

小白-HP.4 模块的引用与裁剪

#define MaxVertexNum 100//最大顶点数设置为100 #define INFINITY 65535//无穷大设为双字节无符号整数的最大值65535 typedef int Vertex//用顶点下标表示顶点，为整型 typedef int WeightType;//边的权值设为整型 //边的定义 typedef struct ENode *PtrToENode; struct ENode{ 
    Vertex V1,V2;//有向边<V1,V2> WeightType Weight;//权重 }; typedef PtrToENode Edge; //图结点的定义 typedef struct GNode *PtrToENode; struct GNode{ 
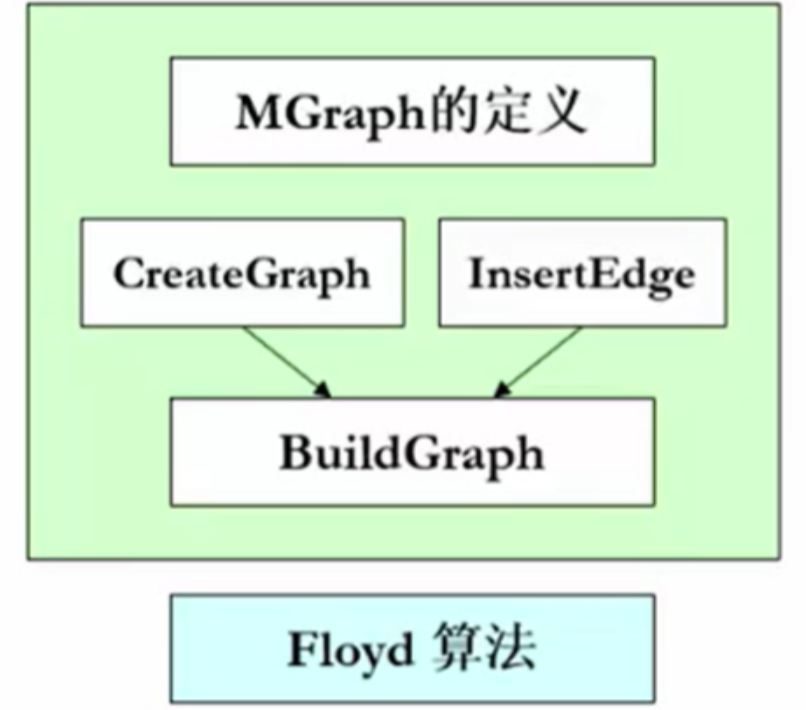
    int Nv;//顶点数 int Ne;//边数 WeightType G[MaxVertexNum][MaxVertexNum];//邻接矩阵 DataType Data[MaxVertexNum];//存顶点的数据 //注意：很多情况下，顶点无数据，此时Data[]可以不出现 }; typedef PtrToENode MGraph;//以邻接矩阵存储的图类型 

CreateGraph原始代码

MGraph CreateGraph(int VertexNum) { 
   /*初始化一个有VertexNum个顶点但没有边的图*/ Vertex V,W; MGraph Graph; Graph=(MGraph)malloc(sizeof(struct GNode));/*建立图*/ Graph->Nv VertexNum; Graph->Ne = 0; /*初始化邻接矩阵*/ /*注意：这里默认顶点编号从0开始，到(Graph->Nv-1)*/ for (V=0; V<Graph->Nv; V++) for (W=0; W<Graph->Nv; W++) Graph->G[V][W] = INFINITY; return Graph; } void InsertEdge(MGraph Graph,Edge E) { 
    /*插入边<V1,V2>*/ Graph->G[E->V1][E->V2] = E->Weight; /*若是无向图，还要插入边<V2,V1> 因为是无向图，所以我们需要把读进来的这个权重同时赋予矩阵里面两个元素*/ Graph->G[E->V2][E->V1] = E->Weight; 

MGraph BuildGraph() { 
    MGraph Graph; Edge E; Vertex V; int Nv,i; scanf("%d",&Nv);//读入顶点个数 Graph = CreateGraph(Nv);//初始化有Nv个顶点但没有边的图 scanf("%d",&(Graph->Ne));//读入边数 if(Graph->Ne != 0 ){ 
   //如果有边 E = (Edge)malloc(sizeof(struct ENode));//建立边结点 //读入边，格式为"起点 终点 权重"，插入邻接矩阵 for(i=0;i<Graph->Ne;i++){ 
    scanf("%d %d %d",&E->V1,&E->V2&E->Weight);//读进来的时候，编号是从1开始的 //注意：；如果权重不是整型，Weight的读入格式要改 E->V1--; E->V2--;//读进来的编号都-1，那就变成起始编号从0开始的了，原本1变成0，2变成1，依次变化 InsertEdge(Graph,E);//插入边的时候，图默认顶点的编号是从0开始 } } //如果顶点有数据的话，读入数据。没有的话这个for循环可以删掉 for(V=0;V<Graph->Nv;V++) scanf(" %c",$(Graph->Data[V])); return Graph; } 

问：图的顶点从0开始编号，而本题目中动物从1开始编号。读输入时该如何处理使得图的相关模块可以顺利应用？

答案：E->V1–; E->V2–;

标准的Floyd算法

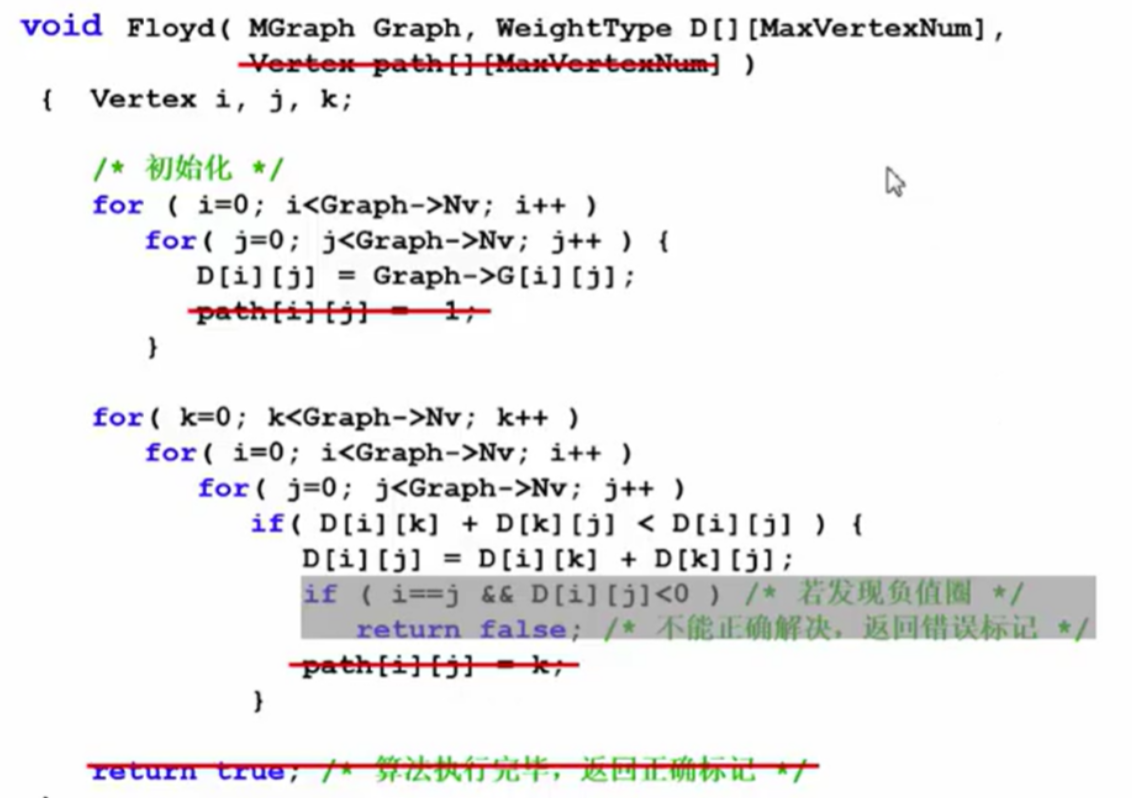
bool Floyd(MGraph Graph ,WeightType D[][MaxVertexNum],Vertex path[][MaxVertexNum])//返回布尔值(bool) { 
    Vertex i,j,k; //初始化 for(i = 0;i<Graph->Nv;i++) for(j = 0;j<Graph->Nv;j++){ 
    D[i][j] = Graph->G[i][j]; path[i][j] = -1; } for(k = 0;k <Graph->Nv;k++) for(i=0;i<Graph->Nv;i++) for(j=0;j<Graph->Nv;j++) if(D[i][k] + D[k][j] < D[i][j]){ 
    D[i][j] = D[i][k] + D[k][j]; if( i == j && D[i][j]<0)//若发现负值圈，从i出发，走了一圈又回到i，这个最短距离是一个负的值，也对应了一个负值圈 return false;//不能正确解决，返回错误标记 path[i][j] = k; } return true;//算法执行完毕，返回正确标记 } 

在本题中进行的改动部分：