数据分析基础-统计学

大家好，欢迎来到IT知识分享网。

1. 变量
   我们需要了解几个名词：
   变量、常量、连续变量、离散变量、连续数据、离散数据、自变量、因变量、函数、单值函数、多值函数
   以上名词大家都比较理解，我这边就解释下什么是单值函数和多值函数：
   单值函数：若对定义域每一个自变量x，其对应的函数值f(x)是唯一的，则称f(x)是单值函数。
   多值函数：若│f(x)│=2x-1，则f(x)=±(2x-1)，一个自变量x对应两个函数值。
   
   
   
   
   
2. 频数分析
   数组阵列：原始数据按照数据大小升序或降序排列，最大值与最小值的差为全距；
   组距、组限、组界、组中值、直方图与频率多边形
   频率分布 = 某一组频数/总频数
   累计频数分布/累计频数表，累计频数多边形/卵形线
   累计频率分布/百分率累计频数 = 累计频数/总频数
   
   
   
   
   
3. 均值、中位数、众数（集中趋势的度量）
   平均值/集中趋势的度量：趋向落在根据数值大小排列的数据的中心
   算数平均：
   
   N个数的算术平均简称均值
   加权算术平均：
   
   
   
   
   

均值、中位数和众数之间的关系：

几何平均G：

调和平均H：


均方根RMS

4. 标准差和其他表示利差的度量
   离差/变差：
   数值数据围绕其平均值分布的分数与集中程度，常用的有全距、平均偏差、半内四分位数间距，10-90百分位数间距、标准差；
   全距：最大值-最小值
   平均偏差
   
   半内四分位数间距：
   
   10-90百分位数间距：
   
   标准差：
   
   
   
   
   
   
   
   
   
   
   
   

9. 统计估计理论
   无偏估计：如果一个统计量的抽样分布的均值等于相应的总体参数，那个这个统计量参数就是此参数的一个无偏估计量；否则，就称为有偏估计量。统计量的相应值分别称为无偏估计或有偏估计，估计量也常简称为估计。
   有效估计：如果两个统计量的抽样分布有相同的均值（或期望），那么方差较小的那个统计量称为此均值的有效估计量，另一个称为无效估计量。统计量的相应值称为有效估计或无效估计。
   在均值的所有无偏估计量中，方差最小的那个统计量常被称为此均值的最有效估计量或最优估计量。
   点估计和区间估计：如果一个数来估计总体的参数，那么这种估计叫做参数的点估计。如果给出两个数，指出参数位于其间，那么这种估计叫做参数的区间估计。
   区间估计更加精确，因为要优于点估计。
   
   
   
   
   
10. 统计决策理论
    统计假设、零假设/原假设、备择假设
    假设检验、显著性检验/决策法则
    第一类和第二类错误：
    当我们拒绝了一个本应接受的假设时，我们就犯了第一类错误，反之，当我们接受了一个本应拒绝的假设时，我们就犯了第二类错误。无论是哪种情形，在判断上我们都犯了错误，做出了错误的决策。
    正态分布的检验，双边检验和单边检验，特殊检验
    
    
    
    
    
11. 小样本理论
    样本容量N<30时，我们称为小样本，对小样本统计量的抽样分布的研究称之为小样本理论，得到的结论不仅适用于小样本问题，也适用于大样本问题，也称为精确抽样理论。
    （注意：这边的t分布，卡方分布，F分布都没有很清楚的解释）
    
    
12. 曲线拟合和最小二乘法
    
    
    
    

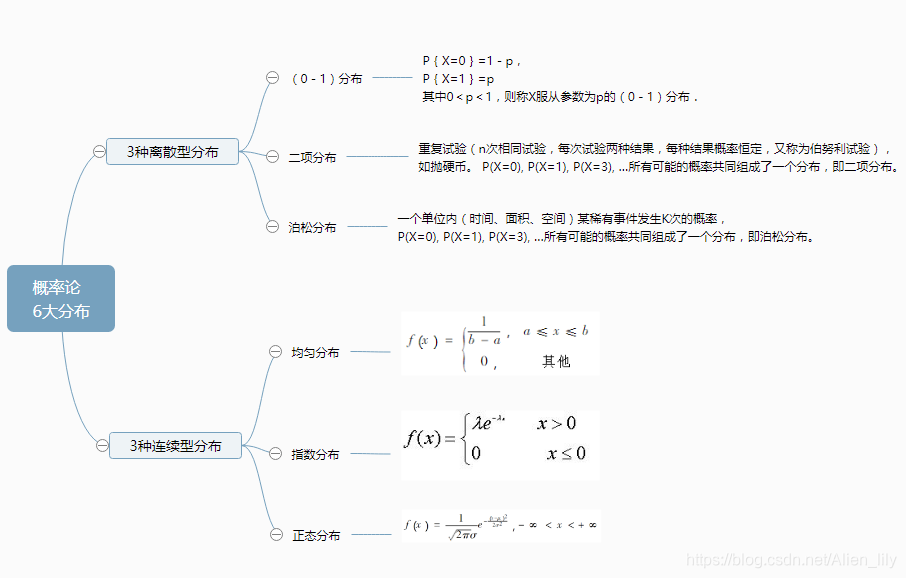
概率论中的六种常用分布，即（0－1）分布、二项分布、泊松分布、均匀分布、指数分布和正态分布。