大家好，欢迎来到IT知识分享网。
P帕塞瓦尔定理指出，一个信号所含有的能量（功率）恒等于此信号在完备正交函数集中各分量能量（功率）之和。它表明信号在时域的总能量等于信号在频域的总能量，即信号经傅里叶变换后其总能量保持不变，符合能量守恒定律。
Plancherel’s theorem编辑
假定
A(
x)和
B(
x）
都是平方可积的（参照 勒贝格测度
）复变函数，且定义在
R
上周期为2π的区间上，分别写成傅里叶级数的形式：
A(
x)和
B(
x）
都是平方可积的（参照 勒贝格测度
）复变函数，且定义在
R
上周期为2π的区间上，分别写成傅里叶级数的形式：
则有：
物理学和工程学上使用的记号
在 物理学 和 工程学 中, 帕塞瓦尔定理通常描述如下:
其中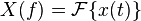
为 x(t) 的连续傅立叶变换（以归一化酉形式），而f代表x的频率分量（非角频率）
帕塞瓦尔定理的此表达形式解释了波形x(t)依时间域t累积的总能量与该波形的傅立叶变换X(f)在频域域f累积的总能量相等。
对于离散时间信号，该理论表达式变换为：
![\sum_{n=-\infty}^\infty | x[n] |^2 = \frac{1}{2\pi} \int_{-\pi}^\pi | X(e^{i\phi}) |^2 d\phi](http://upload.wikimedia.org/math/1/7/4/1747ac6e2c1bfde886693070da5c84c4.png "帕塞瓦尔定理(能量守恒定理)插图10")
其中，X为x的离散时间傅立叶变换(DTFT)，而Φ为x的角频率（度每样本）。
此外，对于离散傅立叶变换 (DFT)，表达式变换为：
![\sum_{n=0}^{N-1} | x[n] |^2 = \frac{1}{N} \sum_{k=0}^{N-1} | X[k] |^2](http://upload.wikimedia.org/math/d/d/3/dd3e997e03ee61f3c43c2e96731deb83.png "帕塞瓦尔定理(能量守恒定理)插图12")
其中，X[k]为x[n]的DFT变换，变换前后样本长度皆为N。
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/136552.html
