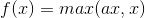神经网络：第一层

大家好，欢迎来到IT知识分享网。

1人工神经网络

2神经网络的相关概念

2.1 输入层、隐含层，输出层

2.2 激活函数

活函数是神经网络设计的核心单元，激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。激活函数需要满足一下几个条件：

1.非线性。如果激活函数是线性的，那么不管引入多少隐层，其效果和单层感知机没有任何差别。

2.可微性。训练网路时使用的基于梯度的优化方法需要激活函数必须可微。

3.单调性。单调性保证了神经网络模型简单。

1. sigmod函数

当然，流行也是曾经流行，这说明函数本身是有一定的缺陷的。

1. 当输入稍微远离了坐标原点，函数的梯度就变得很小了，几乎为零。在神经网络反向传播的过程中，我们都是通过微分的链式法则来计算各个权重w的微分的。当反向传播经过了sigmod函数，这个链条上的微分就很小很小了，况且还可能经过很多个sigmod函数，最后会导致权重w对损失函数几乎没影响，这样不利于权重的优化，这个问题叫做梯度饱和，也可以叫梯度弥散。
2. 函数输出不是以0为中心的，这样会使权重更新效率降低。对于这个缺陷，在斯坦福的课程里面有详细的解释。
3. sigmod函数要进行指数运算，这个对于计算机来说是比较慢的。

2.tanh函数

tanh是双曲正切函数，tanh函数和sigmod函数的曲线是比较相近的，咱们来比较一下看看。首先相同的是，这两个函数在输入很大或是很小的时候，输出都几乎平滑，梯度很小，不利于权重更新；不同的是输出区间，tanh的输出区间是在(-1,1)之间，而且整个函数是以0为中心的，这个特点比sigmod的好。

一般二分类问题中，隐藏层用tanh函数，输出层用sigmod函数。不过这些也都不是一成不变的，具体使用什么激活函数，还是要根据具体的问题来具体分析，还是要靠调试的。

3.ReLU函数

ReLU(Rectified Linear Unit)函数是目前比较火的一个激活函数，相比于sigmod函数和tanh函数，它有以下几个优点：

1. 在输入为正数的时候，不存在梯度饱和问题。
2. 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）

当然，缺点也是有的：

1. 当输入是负数的时候，ReLU是完全不被激活的，这就表明一旦输入到了负数，ReLU就会死掉。这样在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，这个和sigmod函数、tanh函数有一样的问题。
2. 我们发现ReLU函数的输出要么是0，要么是正数，这也就是说，ReLU函数也不是以0为中心的函数。

4.ELU函数

ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

5.PReLU函数

PReLU函数公式和曲线如下图

PReLU也是针对ReLU的一个改进型，在负数区域内，PReLU有一个很小的斜率，这样也可以避免ReLU死掉的问题。相比于ELU，PReLU在负数区域内是线性运算，斜率虽然小，但是不会趋于0，这算是一定的优势吧。

我们看PReLU的公式，里面的参数α一般是取0~1之间的数，而且一般还是比较小的，如零点零几。当α=0.01时，我们叫PReLU为Leaky ReLU，算是PReLU的一种特殊情况吧。

2.3 权重和偏置

假设神经元输入是X = [x1,x2,x3]，权重为w,偏置为b, 那么其输出为

可以看出,w，b会影响感知机的输出结果，正是因为此神经网络在迭代过程中修改的是权重w和偏置b
g(wx+b)，其中w,x均为向量.比如下图所示：

加入激活函数为g(x)，我们就可以用公式g(w1x1+w2x2+b)
激活函数用的是sigmoid函数

将输入映射到一个(0,1)的输出范围

现在我们还是有一个简单的任务，需要将下面三角形和圆形进行分类：
利用上面神经元训练可以得到一个直线，去线性分开这些数据点.方程如下：
w1x1+w2x2+b=0，我们就可以得到下面这条类似的直线去线性分割好俩种不同类型的数据点.

那么这条边界找到了.而这个边界是w1x1+w2x2+b=0的方程，而w1x1+w2x2+b是作为激活函数sigmoid的输入处理.
激活函数将这个输入映射到(0,1)的范围内.那么可以增加一个维度来表示激活函数的输出.
我们认为g(x)>0.5就为正类（这里指圆形）,g(x)<0.5就为负类，这里指三角形类.得到的三维图如下

右边输出为1的部分就是说w1x1+w2x2+b>0,导致激活函数输出>0.5，从而分为正类（ 圆形类）,左边输出为-1的部分就是说w1x1+w2x2+b<0,导致激活函数输出<0.5，从而分为负类（ 三角形类）
其中w参数的作用，我们可以得到，是决定那个分割平面的方向所在.分割平面的投影就是直线w1x1+w2x2+b=0
我们解释如下，在二个输入中，可以得到w=[w1,w2],令方程w1x1+w2x2+b=0，那么该直线的斜率就是-w1/w2。随着w1,w2的变动，直线的方向也在改变，那么分割平面的方向也在改变~
其中b参数的作用，是决定竖直平面沿着垂直于直线方向移动的距离，当b>0的时候，直线往左边移动，当b<0的时候，直线往右边移动.
我们通过例子解释如下：首先我们可以肯定是直线方向不变，因为我们没有动斜率的任何参数，只是改变b，要说明的就是为什么当b>0的时候，直线往左边移动，当b<0的时候，直线往右边移动.
假设我们有直线方程x1+x2-3=0,画出这个图像如下

此时我们将b减小到0，图像变为如下
当b>0的时候，直线往左边移动，当b<0的时候，直线往右边移动.
我先不说为什么一定要加入偏置b,就还是上面的分类问题，假如我现在的样本点是如下这种

此时我们希望得到的线性方程分割线是下面这种，能够正确的将俩类进行分开：

2.4 损失函数

2.5 反向传播（Back Propagation,BP）算法