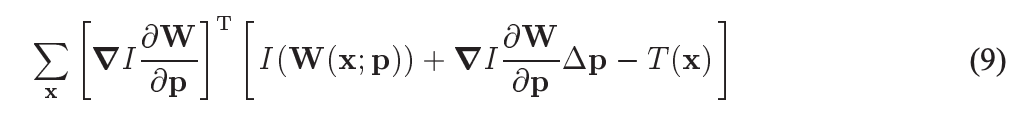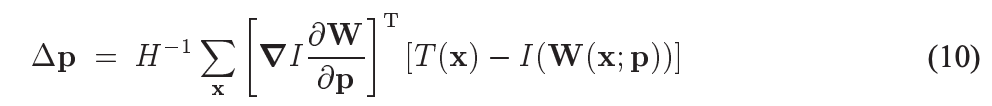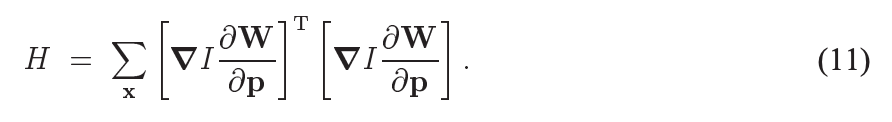详解LK光流法（含金字塔多层光流），反向光流法（附代码）

大家好，欢迎来到IT知识分享网。

这就要求光照恒定，物体反射恒定，是个很强的假设。

现在要估计的是运动偏移量[dx, dy]，也就是光流。仅用一个点无法解，一般会取一个窗口内的像素，考虑它们具有相同的运动。

上面就是最小二乘法求光流的大概步骤，具体如何求$\Delta p$，下面是高斯牛顿法解$\Delta p$，及迭代出光流(dx, dy)的步骤：

1. 把上面的(4)式，也就是cost函数，对$I(W(x;p+\Delta p))$进行一阶泰勒展开，得到：
   
   这里的$▽I$指在图像 I，也就是img2中对特征点处求x，y方向上的梯度，然后通过W变换回T的坐标中。
   $\partial W/\partial p$指W对p求偏导。
   举个例子吧，假如W如下
   
   那么$$\left[\begin{array}{cc}\partial W_x/\partial p1& \partial W_x/\partial p2\\ \partial W_y\partial p1& \partial W_y/\partial p2\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$
   上面的(p1, p2)就是我们要求的光流(dx, dy), 这个$\partial W/\partial p$就是雅可比矩阵$J$
   
   
   
   
   
   
   
2. 上面（6）式对$\Delta p$求偏导，得到：
   
   先解释一下$\Delta p$和上面p的关系，上面的p是我们要求的光流(dx, dy)，而直接求比较困难，现在假设已经知道初始的(dx, dy), 比如(0, 0)，要通过每次求(dx, dy)的增量($\Delta dx,\Delta dy)$, 也就是$\Delta p$，来不断修正(dx, dy), 直到收敛。
   另上面(9)式偏导为0，可求得：
   
   这就是最小二乘法的解，
   其实可以想到最小二乘法解增量问题的形式一般是
   $H\Delta x=b$, 其中
   $H=J{J}^T,b=-Je$, $e$即为error函数。
   
   
   
   
   
   
   
   

同样地，上面的$H=J{J}^T$,

$\Delta p$一旦求出，就可以不断迭代，得到最终的光流(dx, dy), 也就是p了。

下面通过一个例子说明如何追踪特征点的光流。

先在img1，也就是T里提取特征点kp1

Mat img1 = imread("../imgs/LK1.png", 0); //T Mat img2 = imread("../imgs/LK2.png", 0); //I //key points vector<KeyPoint> kp1; FAST(img1, kp1, 40); //可以用其他特征点 

对每个特征点kp1[i], 设初始(dx, dy) = (0, 0)

auto kp = kp1[i]; double dx = 0, dy = 0; //需要估计 

要用到的几个矩阵

Eigen::Matrix2d H = Eigen::Matrix2d::Zero(); //Hessian Eigen::Vector2d b = Eigen::Vector2d::Zero(); //bias Eigen::Vector2d J; //Jacobian 

//计算cost和jacobian for(int x = -half_patch_size; x < half_patch_size; x++) { 
    for(int y = -half_patch_size; y < half_patch_size; y++) { 
    double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) - GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy); if(inverse == false) { 
    //error分别对dx, dy求导，因为是离散的，所以用dx+1,dx-1的位移差，dy同样 //x, y是窗口内的偏移量 //img1中没有dx, dy的变量，所以只有img2 J = -1.0 * Eigen::Vector2d( 0.5 * (GetPixelValue(img2, kp.pt.x + x + dx + 1, kp.pt.y + y + dy) - GetPixelValue(img2, kp.pt.x + x + dx - 1, kp.pt.y + y + dy)), 0.5 * (GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy + 1) - GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy - 1)) ); }else if (iter == 0) { 
    //反向光流法，只需计算第一次的H，后面H固定 J = -1.0 * Eigen::Vector2d( 0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) - GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)), 0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) - GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1)) ); } //计算H, b and set cost b += -error * J; cost += error * error; //正向光流法每次迭代都要更新H if(inverse == false || iter == 0) { 
    H += J * J.transpose(); } } 

$\Delta p=H^{-1}b$

Eigen::Vector2d update = H.ldlt().solve(b); //避免求矩阵的逆 //最小二乘收敛 if(iter > 0 && cost > lastCost) { 
    break; } 

迭代更新(dx, dy)

dx += update[0]; dy += update[1]; lastCost = cost; 

最后(dx, dy)就是我们要求的光流，根据img1中的keypoint kp1, 可以追踪到img2中的keypoint坐标为

kp2[i].pt = kp.pt + Point2f(dx, dy); 

以上是单层光流，下面说说金字塔的多层光流
假设左边最下面一层(3号）是原图像img1 (T), 那么往上（2号，1号）就是对img1的缩放，右边最下面一层是img2, 往上是对img2的缩放。

double pyramid_scale = 0.5; //create pyramids vector<Mat> pyr1, pyr2; //image pyramids for(int i = 0; i < pyramids; i++) { 
    if(i == 0) { 
    pyr1.push_back(img1); pyr2.push_back(img2); } else { 
    Mat img1_pyr, img2_pyr; //cv::Size（列，行） resize(pyr1[i - 1], img1_pyr, Size(pyr1[i-1].cols * pyramid_scale, pyr1[i-1].rows * pyramid_scale)); resize(pyr2[i - 1], img2_pyr, Size(pyr2[i-1].cols * pyramid_scale, pyr2[i-1].rows * pyramid_scale)); pyr1.push_back(img1_pyr); pyr2.push_back(img2_pyr); } } 

double dx = 0, dy = 0; //需要估计 if(has_initial) { 
    dx = kp2[i].pt.x - kp.pt.x; //x位移 dy = kp2[i].pt.y - kp.pt.y; //y位移 } 

这样做有什么好处呢？假设移动了20个像素，直接求光流可能由于变化太大而陷入局部极值；但是缩放之后可能就只移动了5个像素，这就是一种coarse to fine的思想。

现在来说逆向光流法，
前面正向光流每迭代一次都要计算一次H，计算量很大。考虑有没有一种方法可以只计算一次H，然后后面都用这个H。
逆向光流法是前面正向光流的逆向，也就是交换一下方向，现在是从I 反向回到T，也就是从运动之后的 I 变换回运动前的T。
引用一个图方便理解

}else if (iter == 0) { 
    //反向光流法，只需计算第一次的H，后面H固定 //H只和T,也就是img1有关 J = -1.0 * Eigen::Vector2d( 0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) - GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)), 0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) - GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1)) ); } 

每次迭代中H不需再更新

if(inverse == false || iter == 0) { 
    H += J * J.transpose(); }