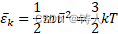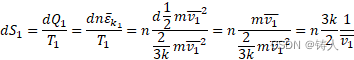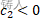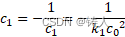关于如何实现熵减

大家好，欢迎来到IT知识分享网。

熵，这里说的是热力学第二定律里的熵。

它被定义为，

其中 为玻尔兹曼常数，

为一个纯数，可知 和 具有相同的量纲，都是焦耳每开尔文。

所以熵的单位为能量单位和热力学温度单位的比值，或者说（对于气体来说）单位热力学温度对应的能量。

然而我们通常不使用熵的数值而是它的变化量，比如物体在热力学温度为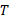 的时候获得热量为 ，这时对应的熵增为（假定没有对外或者对内做功），

它的微分形式为，

现在我们假定考虑的物体仅为理想气体，此时可以知道，理想气体的分子平均动能为

可知

而理想气体的能量为平均动能乘以分子数量，

其中 为气体分子的数量。现在让我们考虑一下，在气体分子数量不变的前提下，系统的熵增会如何发生。

把具有不同温度但气体分子数量相同的两种气体1和2，混合放置在一个封闭环境中构成封闭系统，此时，

由于温度不同，混合气体一定会发生1到2的热传递（因为 ），在微观来说，显然是通过两种气体分子的碰撞（电磁作用）来实现的。既然熵可以被认为是某个平均值在能量和温度上的体现的比值，我们可以尝试写出，对于1和2的熵变，

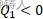
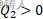
气体1温度高，会放热，其熵变是小于0的（因为 ），而这个热量一定被气体2获取，所以气体2的熵变是大于0的（ ），而热量不会跑出封闭系统，所以可以知道，

所以系统的总的熵变为

再加上， ，由此可知，

这是显然的，因为气体1的温度高，就对应了气体1的平均分子速率要高。一般来说，考虑熵增，我们是不去考虑单个分子的；但是从上式可以看出，即便就考虑两个分子，也是可以的，我们就把这两个分子当成两种气体，它们各自的运动速率就是两种气体的平均运动速率。此时，我们就可以把熵增量子化，也即是考虑单个分子之间的关系，并用这种关系重新定义熵。

将上式抽象化，我们去掉平均符号，就得到了两个气体分子之间的熵关系，为了保证其为正值，要增加绝对值 运算，而且要知道这里说的都是速率，负号就是减号，不代表方向。当然此时 ，就不用再写了，

可见只要速度为实数，则必有

这说明，对于两个气体分子而言，它们的相对速度差异越大，那么它们之间构成的熵增的数值就越大。而如果两个气体分子的运动速率相等，则熵增为0，也就是说熵增停止。换句话说，熵增对应于两个气体分子之间运动速率的差异。可见，当所有的分子运动速率都几乎一样的时候，熵增也就停止了。而这就是热平衡状态。

现在让我们引入狭义相对论，尝试将速率的关系转化为绝对速度之间的关系，

可见经过代换之后，

也就是说，相对速度构成熵增和绝对速度构成熵增，具有一致的形式。这时候我们只需要考虑绝对速度的差异部分

可见，用这种方式来考虑问题，熵减是完全不可能的：既然常规的方法之下熵减不可能，那么有没有可能在量子层面实现熵减呢？也就是说，让单个或者两个气体分子实现熵减，然后聚集这种熵减的效应，最终形成宏观上的熵减效应呢？

让我们继续仔细考虑，要使得，

成立，情况就只有，

具体来说，有可能是两者异号，

这时候， 体现为，

两者的相对速度为，

这种情况，分子1为光速，而分子2为静止。这样两个分子构成的系统是熵减的。但这个情况似乎没有意义。

还有一种情况，（此处引入 和 应避免和玻尔兹曼常数 相混淆）

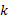
也就是两种光速都为虚数光速，

这个数值应当是小于0的，但是这时候又引入了虚数单位。我们知道光速其实也是虚数单位，可以尝试让，

此时熵减是必然的，而且仅由两个比例常数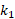 和 决定，

也就是说，若要实现熵减，则两个分子各自的绝对速度，要达到本地光速平方的数量级。这个数量显然大于光速周期，所以它只能体现为其负倒数的形式，也就是说，

而这个负倒数，其绝对值显然已经小于真空光速的倒数的绝对值。这是什么意思呢？意思就是说，这样的气体分子，运动的速度是比光速还略大一点的，但不能完成周期。

也就是说，比本地时空光速略大一点，比周期略小一点的情况。可以认为这个数值相当大，超过光速，或者极其小，比静止还静止。那么这个数值到底对应了什么呢？根据来自于电磁学的经验，具有这种绝对速度的，我们知道它就是磁场。

具体来说，我们需要两种分子。这两种分子都可以受到磁场的影响，其速率的取值，可见下图，

可见 和 两者越是接近于0，且差异较大，熵减就越大。所以我们可以使用两种频率的磁场，分别对两种气体分子进行加速，或者两种脉宽的磁场，在两个方向上对同种气体分子进行加速，使得它们产生需要的速度差异。而磁场本身就具有 的性质，只需要调节不同的 和 即可。

考虑到熵增最终导致所有气体分子温度相等，那么熵减则可以有效的产生温度不相等的气体分子，也就是说，可以实现将气体分子的动能转移到特定气体分子上面（比如 或者 ）而若磁场可以影响气体分子的运动速率，则气体分子的运动速率也一定可以反向影响磁场，这就提供了用磁场获取气体分子动能的途径。再将磁场获取的能量转化为对应的电能，则可以实现对空间热能的提取（这里最先想到的，显然是如何解决全球变暖的问题了）。

熵增的本质，在分子层面上就是其绝对速度的趋同；熵减的本质相反，就是绝对速度的趋异。趋同导致秩序的失去（方向杂乱），趋异导致秩序的建立（有特定方向）。

熵增不是必然的，熵增是电性振动主导前提下分子相对运动造成的效果；而若是磁性振动主导为前提，则熵减才是必然的。