数据结构——【图的入门】

大家好，欢迎来到IT知识分享网。

目录

图的定义

无向图

无向图的实现​

深度优先搜索

广度优先搜索

图的定义

定义∶图是由一组顶点和一组能够将两个顶点相连的边组成的

特殊的图:
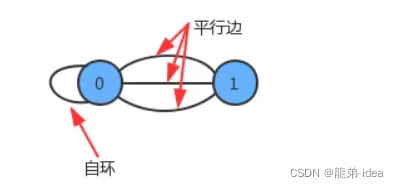
1.自环:即一条连接一个顶点和其自身的边;

2.平行边∶连接同一对顶点的两条边;

 图的分类:

按照连接两个顶点的边的不同，可以把图分为以下两种:

无向图

相邻顶点∶
当两个顶点通过一条边相连时，我们称这两个顶点是相邻的，并且称这条边依附于这两个顶点。

度∶
某个顶点的度就是依附于该顶点的边的个数

子图:
是一幅图的所有边的子集(包含这些边依附的顶点)组成的图;

路径∶
是由边顺序连接的一系列的顶点组成

环∶
是一条至少含有一条边且终点和起点相同的路径

连通图∶
如果图中任意一个顶点都存在一条路径到达另外一个顶点，那么这幅图就称之为连通图
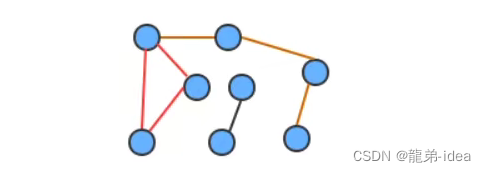
连通子图:
一个非连通图由若干连通的部分组成，每一个连通的部分都可以称为该图的连通子图

 图的存储结构
要表示一幅图，只需要表示清楚以下两部分内容即可∶
1.图中所有的顶点;
⒉.所有连接顶点的边;
常见的图的存储结构有两种∶邻接矩阵和邻接表

邻接矩阵
1.使用一个V*V的二维数组int[V][v]adj,把索引的值看做是顶点;
⒉.如果顶点v和顶点w相连，我们只需要将adj[v][w]和adj[w][v]的值设置为1,否则设置为0即可。

很明显，邻接矩阵这种存储方式的空间复杂度是V^2的，如果我们处理的问题规模比较大的话，内存空间极有可能不够用。
邻接表
1.使用一个大小为V的数组Queue[V]adj，把索引看做是顶点;
2.每个索引处adj[v]存储了一个队列，该队列中存储的是所有与该顶点相邻的其他顶点

很明显，邻接表的空间并不是是线性级别的，所以后面我们一直采用邻接表这种存储形式来表示图。

无向图的实现

import java.util.LinkedList; import java.util.Queue; public class Graph { private final int V; //顶点数量 private int E; //边的数量 private Queue<Integer>[] adj; public Graph(int V){ //初始化 this.V = V; this.E = 0; this.adj = new LinkedList[V]; for(int i=0; i<adj.length; i++){ adj[i] = new LinkedList(); } } public int V(){ return V; } public int E(){ return E; } public void addEdge(int v, int w){ // 无向图 adj[v].offer(w); adj[w].offer(v); // 边的数量+1 E++; } public Queue<Integer> adj(int v){ return adj[v]; } }

图的搜索
在很多情况下，我们需要遍历图，得到图的一些性质，例如，找出图中与指定的顶点相连的所有顶点，或者判定某个顶点与指定顶点是否相通，是非常常见的需求。
有关图的搜索，最经典的算法有深度优先搜索和广度优先搜索

深度优先搜索

所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，然后找兄弟结点。

 很明显，在由于边是没有方向的，所以，如果4和5顶点相连，那么4会出现在5的相邻链表中，5也会出现在4的相邻链表中，那么为了不对顶点进行重复搜索，应该要有相应的标记来表示当前顶点有没有搜索过，可以使用一个布尔类型的数组boolean[V] marked,索引代表顶点，值代表当前顶点是否已经搜索，如果已经搜索，标记为true ，如果没有搜索，标记为false ;

API设计

public class DFS { private boolean[] marked; //数组索引代表顶点，表示当前顶点是否已经被搜索 private int count; // 记录有多少个顶点与顶点s相通 public DFS(Graph G, int s){ //初始化 this.marked = new boolean[G.V()]; this.count = 0; dfs(G,s); } private void dfs(Graph G, int V){ // 把V顶点标识为已经搜索 marked[V] = true; for(Integer w: G.adj(V)){ //判断当前w顶点有没有被搜索过 if(!marked[w]){ dfs(G,w); } } count++; // 相通顶点数量+1 } //判断W顶点是否和S顶点相通 private boolean marked(int w){ return marked[w]; //被搜索过则意味着相通 } //获取与顶点s相同的所有顶点的总数 public int count(){ return count; } }

广度优先搜索

所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后找子结点。

 （搜索过的点不用再搜索）层序遍历其实就是广度优先搜索。

import java.util.LinkedList; import java.util.Queue; public class BFS { private boolean[] marked; private int count; private Queue<Integer> waitSearch; //辅助队列 public BFS(Graph G, int s){ this.marked = new boolean[G.V()]; this.count = 0; this.waitSearch = new LinkedList<Integer>(); bfs(G,s); } private void bfs(Graph G, int v){ marked[v] = true; waitSearch.offer(v); while(!waitSearch.isEmpty()){ Integer wait = waitSearch.remove(); //遍历wait顶点的邻接表 for(Integer w: G.adj(wait)){ if(!marked[w]){ bfs(G, w); } } } count ++; } public boolean marked(int w){ return marked[w]; } public int count(){ return count; } }