波动方程——弦的横振动（牛顿第二定律+胡克定律）| 偏微分方程（二）

大家好，欢迎来到IT知识分享网。

弦的横振动

物理问题：一根弦在内部张力作用下处于平衡位置，某个微小扰动引起部分质点的位移，内部张力又使邻近的部分随之产生位移，形成波的运动。

分析步骤：求解弦的运动，首先要去“去粗存精”，对弦及其运动作“理想化”假设，即建立物理模型。

理想化假设：

1. 弦均匀细长，从而其横截面可忽略而视作线，线密度为常数。
2. 弦柔软弹性，可任意弯曲，张力满足胡可定律。
3. 弦的运动在同一平面内进行，每个质点的位移都是横向的，即垂直于弦的平衡位置，且绝对位移和相对位移都很小。

基本物理定律：

1. 牛顿第二定律
2. 胡克定律

数学模型：

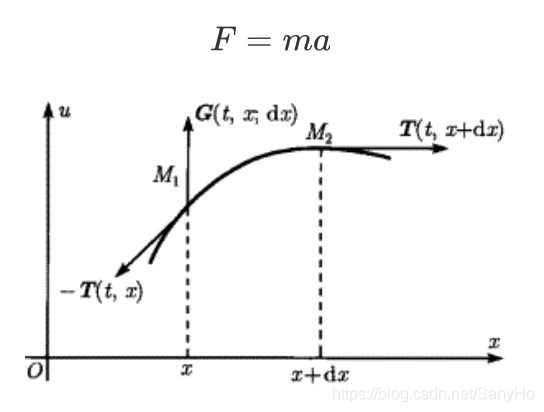
1. 取弦在自身张力作用下的平衡位置所在直线为x轴，横向位移方向为u轴。
2. 设t时刻弦上x处的质点相对于平衡位置的横向位移$u=u(t,x)$为未知函数。
3. 微元分析法：在弦上取微元$[x,x+dx]$，微分记号$dx$表示一个无穷小改变量。此微元可视作质量为$\rho dx$的质点，在他时刻的运动遵循牛顿第二定律。

$$F=ma$$

4. 微元所受的外力有左端点的张力$-T(t,x)$，右端点的张力$T(t,x+dx)$，以及加在微元上的垂直于$x$轴的外力$G(t,x;dx)$。

   如果线密度$\rho$为常数，t时刻作用与x处的单位长度上的外力，即外力密度$g(t,x)$已知，张力$T(t,x)$关于x可微，则微元服从的牛顿第二定律可具体表示为
   $$\begin{gathered} \rho dx\frac{{\partial }^{2}u}{\partial t^2}{\mathbf{u}}^{。}=-\mathbf{T}(t,x)+\mathbf{T}(t,x+dx)+\mathbf{G}(t,x;dx) \\ \approx \frac{\partial \mathbf{T}}{\partial x}dx+g(t,x)dx{\mathbf{u}}^{。} \end{gathered}$$
   其中，第二个等号忽略了$dx$的高阶无穷小。其分量形式为
   $$\frac{\partial T_1}{\partial x}=0\text{\hspace{1em}(1)}$$
   
   
   

   $$\rho \frac{{\partial }^{2}u}{\partial t^2}=\frac{\partial T_2}{\partial x}+g(t,x)\text{\hspace{1em}(2)}$$

   其中，$T_1,T_2$分别是张力$\mathbf{T}$在${\mathbf{x}}^{。}$和${\mathbf{u}}^{。}$方向的分量。这就是弦振动满足的基本偏微分方程组。

总结：推导方程的过程，实际上就是将微元运动满足的物理定律翻译成用已知函数、未知函数及其偏导数表示的数学式子。

推广：凡是弹性介质中微小扰动的传播问题，如弹性杆的纵振动、弹性膜的横振动、声波在空气中的传播等，都可用类似方法导出同一类型的方程，一般表示为
$$\frac{{\partial }^{2}u}{\partial t^2}=a\Delta u+f(t,x),x=(x_1,x_2,...,x_n),n=1,2,3\text{\hspace{1em}(5)}$$
其中，$\Delta ={\sum }_{j=1}^n\frac{{\partial }^2}{\partial x_j^2}$为拉普拉斯算子。此类方程称为

波动方程，弦振动方程（4）被称为一维波动方程。而对于固体弹性波方程、流体波方程、电磁波方程等。在一些重要的特殊情况下，可约化为波动（5）。

思考：弦振动方程（3）是在一定的理想化假设下导出的。如果存在其他不能忽略的因素，比如弦在粘稠液体中振动，阻尼必须考虑，推出的方差中就会增加$\alpha \frac{\partial u}{\partial t}$项。故任何数学模型都是相对的，超出一定范围，则需要建立新的模型。