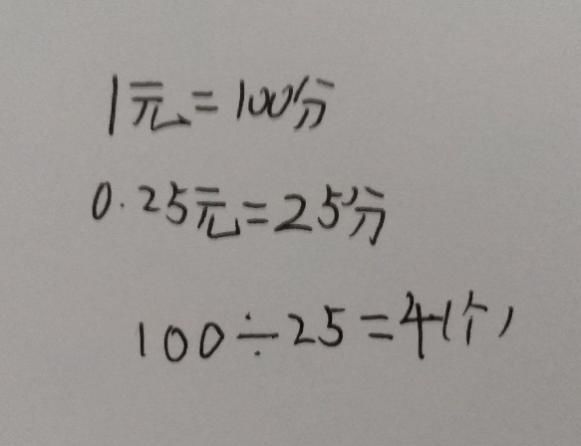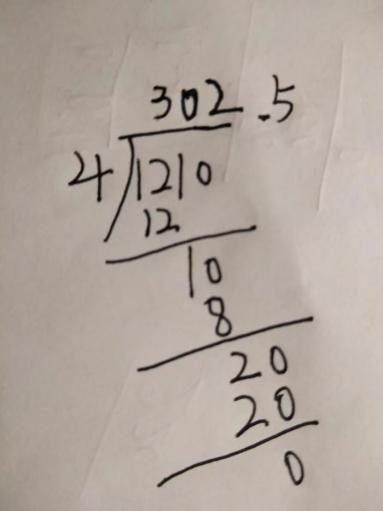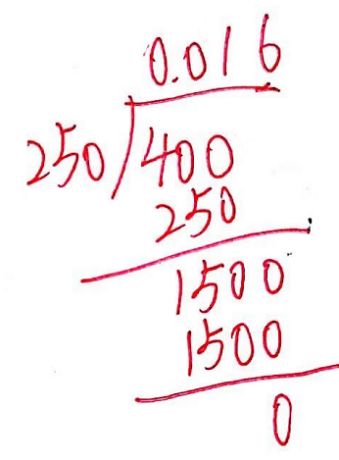小数除以小数的竖式题_小数除以小数

发明数学，创造数学

像数学家一样思考  数学精彩观念的诞生

数学可以越学越容易吗？贞元数学告诉你：当然可以！

编者按：

前边我们已经分享了小数除以整数，孩子们有很多种不同的精彩观念，那么小数除以小数还会有哪些令你眼前一亮的新观念呢？

小数除以小数，孩子们又是如何解决的呢？

涵说，小数除以小数看似比前面几种类型的除法算式要难，但是如果我们理解算理的话一点也不难，比如，1.5÷0.5，我们仍然可以运用商不变的规律，把被除数和除数同时扩大10倍，变成15÷5，最后的答案是3。(课上，老师展示了几道被除数与除数小数位数相同的除法算式，让孩子计算，并说明算理)

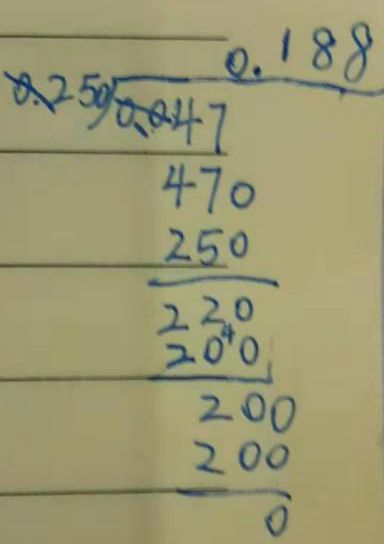
瀚将小数除以小数又细分为三大类：第一类是除数和被除数的小数位数相同，例如，0.47÷0.25，我们可以运用商不变的规律把原算式变成47÷25，且他的算理讲的特别清晰：

47÷25=1(个一)……22(个一)

220(个0.1)÷25=8(个0.1)……20(个0.1)

200(个0.01)÷25=8(个0.01)

1(个一)+8(个0.1)+8(个0.01) =1.88

0.47÷0.25的竖式如下：

课堂反馈：

师：瀚这样列竖式可以吗？

涵：可以，因为0.47÷0.25的结果与47÷25的结果一样，只要计算47÷25的竖式就可以了。

星：我觉得不可以，因为这样看不出来算式原来的模样，别人以为你是在计算47÷25呢！

寒：瀚利用了商不变的规律列竖式，商是不变的，但是他直接改变了原来的算式，让人看不出来这道题其实在计算0.47÷0.25。

师：那怎么办呢？

星：我觉得可以这样写竖式：    

烨：这样写挺好的，既能将0.47÷0.25的竖式转换成47÷25的竖式进行计算，还能让别人知道你计算的就是0.47÷0.25的竖式。

睿：我认为这样太麻烦了，从来没有见过这样的竖式。

涵：或者我们可以把两个数都乘100写在竖式的前面，再列竖式：

瀚：这样也好麻烦呀！

师：我们这样写如何？

生们：哦，我明白了，这样写既简洁，又能明白原算式是0.47÷0.25(接下来，学生独立解决上面这道题)

第二类是除数的小数位数比被除数的小数位数多，例如，0.47÷0.025，我们可以运用商不变的规律把原算式变成470÷25。

47(个十)÷25=1(个十)……22(个十)

220(个一)÷25=8(个一)……20(个一)

200(个0.1)÷25=8(个0.1)

1(个十)+8(个一)+8(个0.1)=18.8

0.47÷0.025的竖式如下：

课堂反馈：

瀚的竖式刚展示出来就遭到质疑，于是，一名同学板书，其他在同学本子上挑战： 

星：不可以，因为被除数扩大了100倍，而除数扩大了1000倍，它们扩大的倍数不同，所以商是会改变的。

睿：应该将被除数与除数同时扩大1000倍，将被除数变成470.

师：除此之外，为了达成统一，我们不仅要把小数点去掉，最好把前面的0也去掉。

接下来请一位同学板书，有问题的同学修改。

第三类是被除数的小数位数多于除数的小数位数，例如，0.047÷0.25，我们可以运用商不变的规律把原算式变成4.7÷25。

47(个0.1)÷25=1(个0.1)……22(个0.1)

220(个0.01)÷25=8(个0.01)……20个(0.01)

200(个0.001)÷25=8(个0.001)             

8(个0.001)+8(个0.01)+1(个0.1)=0.188

0.047÷0.25的竖式如下：

课堂反馈：

师：这道题可以怎样计算呢？

星：可以把被除数和除数同时扩大1000倍，变成47÷250计算。

烨：我认同，这样成功地将小数除法问题转化成整数除法问题了。

瀚：还可以把它们同时扩大100倍，变成4.7÷25来计算。

涵：对的，这样就可以将小数除以小数转化成小数除以整数问题。

师：这两种方法到底哪一种计算起来比较简单呢？我们通过计算比较一下吧！

(同学们计算后，一致认为第二种比较简单，最后达成临时性共识：诸如解决0.47÷0.25；0.047÷0.25；0.47÷0.025这一类的题目时，只要把除数变为整数即可。在我们课上讨论之前，其实瀚已经在他的论文里说的很清楚了)

学习分数除法前，瀚与涵还单独讨论了整数除以小数的问题：

涵说，当他第一次遇到“1÷0.25”这道题的时候懵了，但后来结合实际情境解决了。一块橡皮0.25元，1元能买几块橡皮？可以先把1元和0.25元都转换成用分作单位的数，也就是100分里边有几个25分，这就变成整数除以分数的问题了。其实这就是商不变规律，被除数和除数同时扩大100倍，商不变。

竖式如下：

课堂反馈： 师： 涵，你确定这是1÷0.25的竖式，不是100÷25或者100÷0.25的竖式？ 涵： 通过刚刚的讨论，我已经知道竖式怎么写了。

全班同学挑战1÷0.25的竖式。

瀚说，遇到整数除以小数问题，如121÷0.4，我们可以将其转换成整数除法(121÷4=30.25)进行计算，但是，一定要记得把商再扩大10倍。瀚还说道：可以根据商不变的规律，将121÷0.4转换成1210÷4进行计算，121÷0.4的竖式可以直接写成1210÷4的竖式。

(竖式的问题通过课堂讨论，瀚已经意识到了这样写算式会给别人带来误会。)

课堂反馈：

师：你们认为我们需要再单独讨论整数除以小数的问题吗？

睿：我觉得需要。(大部分同学保持沉默)

瀚：不需要，它其实可以归到小数除以小数类。

烨：我不认同，它们完全不一样呀，一个被除数是整数，一个被除数是小数。

瀚：可是在计算时，我们主要看的是除数，也就是只要将除数变成整数，然后将被除数扩大相同的倍数就可以了。(同学们恍然大悟)

瀚说，整数除以小数其实与小数除以小数一样，只需要根据商不变的规律把除数变成整数就行了，与被除数是否变成整数没有太大关系。至于为什么不把被除数变成整数，我详细地说明一下我的原因：就如同我刚刚说的，小数除以小数分为三类，当被除数与除数的小数位数相同时，我们可以直接将被除数和除数扩大相同的倍数，变成整数除以整数进行计算。当除数比被除数的小数位数多时，仍然可以将被除数与除数扩大相同的倍数变成整数除以整数进行计算。但是，当被除数的小数位数比除数的小数位数多时，例如，0.004÷0.25，除数乘以100就可以变成整数了，而被除数乘以100并不能变成整数，我的方法是将算式变成0.4÷25就行了，不过，有些人可能会觉得为什么不直接变成4÷250呢？第一，被除数不变成整数也可以进行计算，因为在学小数除以小数之前，我们肯定已经会了小数除以整数。其次，数学要求简便，0.4÷25应该比4÷250更简单，而且除数250的这个零会为下面的竖式带来很多的麻烦。比如：

舒还提出了一个特别棒的问题，她问道：小数除以整数的商可能是整数吗？整数除以整数的商可能是小数吗？宋宋老师期待你们的精彩探索哦！