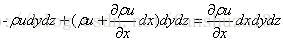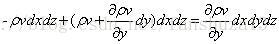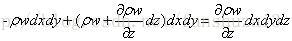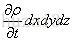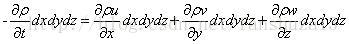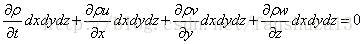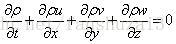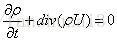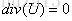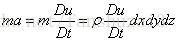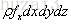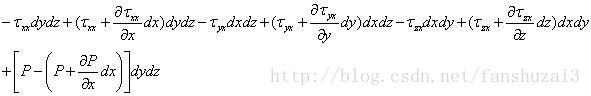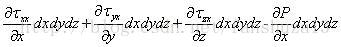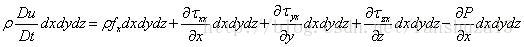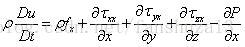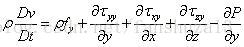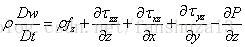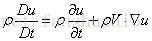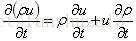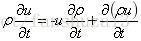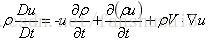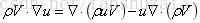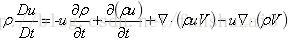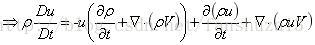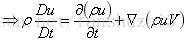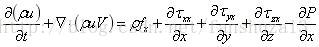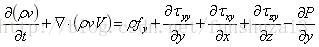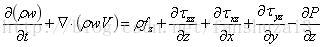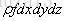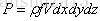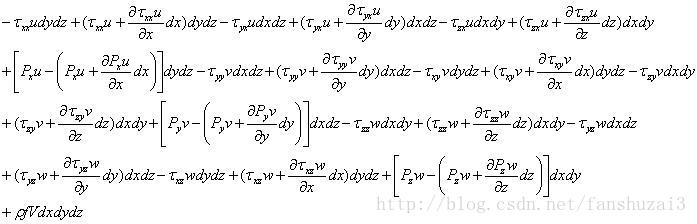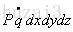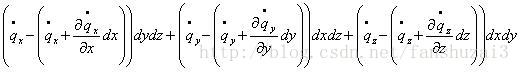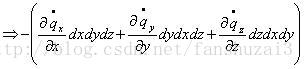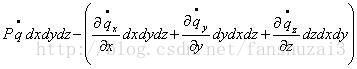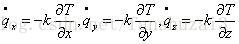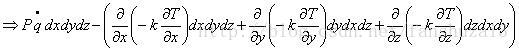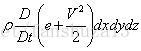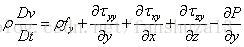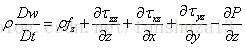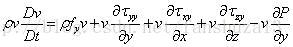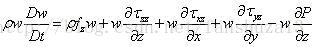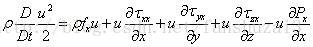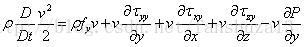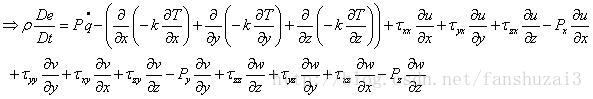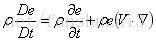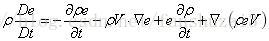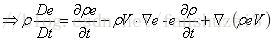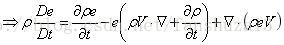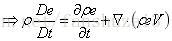大家好,欢迎来到IT知识分享网。
方法取自安德森《计算流体力学基础》
连续性方程
固定流体微元内质量变化率=流体从笛卡尔坐标三个方向流出量
因此可得:
质量变化率:
则:
连续性方程:
用散度表示则可得到:
对于不可压缩流体,其密度为一常数,因此可以得到:
动量方程(纳维-斯托克斯方程)
根据牛顿第二定律可以得出:F=ma;
因此:对于流体微元:
方程式的左边:F=表面力+体积力
方程式的右边,当仅考虑x方向的作用力时:
回到方程式的左边:
体积力可以表示为:
表面力可以表示为流体微元在x方向所有正应力和切应力之和,其表达式如下所示:
整理可得:
将体积力表达式、表面力表达式和方程右边表达式带入牛顿第二定律表达式中可得:
化简可得:
同理可得y方向和z方向的两个方程:
因此可以得到动量守恒方程的非守恒形式:
//注释:
所谓守恒形式和非守恒形式的区别如下:
如果方程可以写成控制方程通用形式: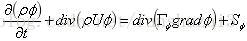
因此,需要通过上述方程继续推导方程的守恒形式:
以x方向为例:
根据:
可得:
将该式子带入上式子:
根据标量与向量的乘积的散度的向量恒等式:
将该式子带入非守恒动量方程表达式得:
同理可得:
因此方程的守恒形式为:
能量守恒方程:
能量守恒方程可以表示为如下形式:
流体微团内能变化率=流入微团的净热流量+体积力和表面力对流体微团的做功的功率
因此,体积力和表面力对流体微团的做功的功率可以表示为:P=Fv
根据动量守恒方程中体积力的描述:体积力=
体积力对流体微元的做功可以表示为:
根据动量守恒方程中表面力的描述:
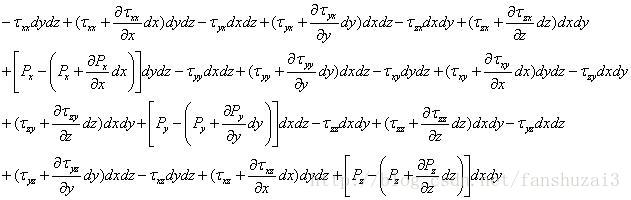
根据表面力做功的功率为:
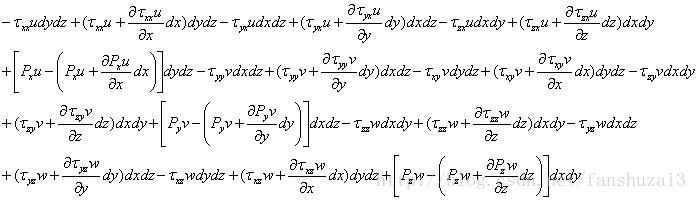
体积力和表面力做功之和为:
流入微团的净热流量:
微团的体积加热为:
热传导引起的热量变化为:
流入微团的净热流量=
根据傅里叶热传导定律:
流体微团内能变化率=
能量守恒方程非守恒形式:
根据动量守恒方程:
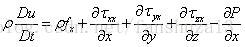
可得:
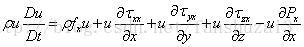
整理得:
将上式子代入到能量守恒方程中,用能量守恒方程减去动量方程推导结果,可以得到:
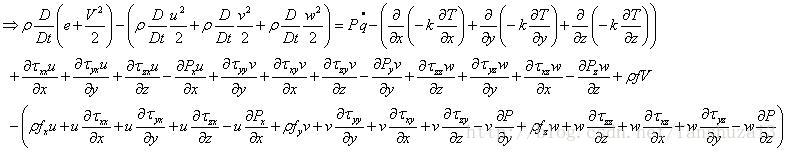
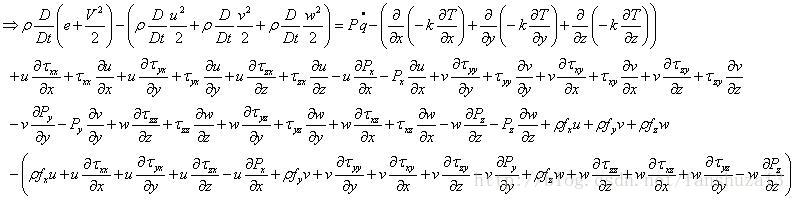
整理得到只有内能表示的能量守恒定律,且消去体积力的能量守恒定律:
根据物质导数的定义:
且:
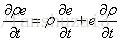
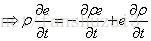
根据: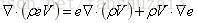
可以得到守恒形式的能量守恒方程:
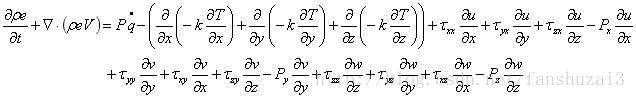
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/140206.html