大家好,欢迎来到IT知识分享网。
目录
一、定积分
定积分用于求解函数在某个区间上的累积效应或面积。
1、定义
表示函数 f(x)在区间 [a,b]上的累积效应或面积。
通过极限推导:
2、几何意义

- 如果 f(x)≥0,则定积分表示曲线下方的面积。
- 如果 f(x)≤0,则定积分表示曲线上方的面积的负值。
3、性质
- 线性性质
- 区间可加性
- 积分上下限交换
- 定积分中值定理:
如果函数 f(x) 在闭区间 [a,b] 上连续,则存在 c∈[a,b],使得:
(证明方法:连续函数的介值定理)
4、基本公式
牛顿-莱布尼茨公式
其中,F(x)是 f(x)的一个原函数,即 F′(x)=f(x)
微积分基本定理
- 如果 f(t) 在区间 [a,b]上连续,则积分上限函数
在区间 [a,b] 上可导,并且其导数为:
- 如果 F(x)是 f(x)的一个原函数,即 F′(x)=f(x),则:
5、换元法
令t = g(x),则有x = 
dx = 
二、多元函数
1、二元极限
1.1定义
设函数 f(x,y) 在点 (a,b) 的某个去心邻域内有定义。如果对于任意给定的正数 ϵ,总存在正数 δ,使得当 
1.2几何意义
当点 (x,y)从任意方式趋近于点 (a,b) 时,函数 f(x,y) 的值趋近于 L。
如果 (x,y)从不同方式趋近于点 (a,b),函数 f(x,y) 的值不相等,则表示 f(x,y) 不存在。
2、偏导数
偏导数表示在多个自变量中,当其中一个自变量改变而其他自变量保持不变时函数值的变化率。
实质上是将其他自变量视为常数,然后按照单变量函数求导的方法进行运算。
定义
设函数 f(x,y) 在点 (x0,y0) 的某个邻域内有定义。如果极限:
存在,则称此极限为函数 f(x,y)在点 (x0,y0) 处对 x 的偏导数,记作:
类似地,如果极限:
存在,则称此极限为函数 f(x,y)在点 (x0,y0)处对 y的偏导数,记作:
计算方法
对于二元函数z=f(x,y),求z对x的偏导数时,将y看作常量,对x求导;求z对y的偏导数时,将x看作常量,对y求导。
3、全微分
定义
如果函数z=f(x, y)在点(x, y)处的全增量
可以表示为
其中A、B不依赖于Δx, Δy,仅与x, y有关,ρ趋近于0(ρ=√[(Δx)²+(Δy)²]),此时称函数z=f(x, y)在点(x, y)处可微分,AΔx+BΔy称为函数z=f(x, y)在点(x, y)处的全微分,记为dz即dz=AΔx +BΔy。
可微的必要条件条件
若z=f(x,y)在(x,y)点处可微,则偏导数 

可微的充分条件
z=f(x,y)在(x,y)的某个邻域内有连续的偏导数

近似计算
z=f(x, y)在点(x, y)处的全增量为
在计算中我们通常使 
即得到近似计算公式:
4、梯度
梯度是一个向量,表示多元函数在某一点处的最大变化率和变化方向。
4.1定义
设 f(x1,x2,…,xn)是一个定义在 Rn(n维欧几里得空间) 上的多元函数,函数 f在n维向量点 a=(a1,a2,…,an)处的梯度定义为:
其中 
4.2性质
- 最大变化率:梯度 ∇f(a) 的方向是函数 f在点 a 处变化率最大的方向。
- 变化率:梯度 ∇f(a) 的大小(模)是函数 f 在点 a 处沿梯度方向的变化率。
沿梯度方向是是函数 f 在点 a 处变化率增加最大的方向;沿梯度反方向是是函数 f在点 a 处变化率减小最大的方向;沿梯度垂直方向函数 f在点 a 处变化率为0。
4.3梯度下降
梯度下降是一种优化算法,用于寻找多元函数的最小值。其基本思想是沿着函数的负梯度方向逐步更新参数,以减少函数值。
算法步骤
- 初始化:选择一个初始点 x0。
- 迭代更新:对于每次迭代 k,计算当前点的梯度
,并更新参数:
其中,η 是学习率(步长),控制每次更新的步幅。
- 终止条件:当梯度的模足够小或达到预设的迭代次数时,停止迭代。 通常,终止条件可以是以下几种:梯度的模足够小、达到预设的迭代次数、函数值变化足够小 。
5、二重积分
二重积分是多元微积分中的一个重要概念,用于计算二维区域上的函数积分。它通常用于计算平面区域上的面积、质量、重心等问题。
二重积分的基本思想是将一个二维区域分割成无数个小区域,然后在每个小区域上计算函数值的积分。
5.1定义
设 f(x,y)f(x,y) 是定义在平面区域 D 上的函数,二重积分记作: 
5.2几何意义
如果 f(x,y)是非负函数,二重积分
5.3二重积分的计算-直角坐标系
在直角坐标系下,二重积分可以表示为两个定积分的乘积:
其中 D 是由 x=a 到 x=b 以及 y=g(x)到 y=h(x) 围成的区域。
5.4二重积分的计算-极坐标系
极坐标系的二重积分计算需要将直角坐标系的坐标转换为极坐标。
极坐标系的基本概念
- 原点:极坐标系的原点称为极点(通常记作 O)。
- 极径:从极点到某一点的距离称为径向距离(通常记作 r)。
- 极角:从极点到某一点的射线与极轴(通常是正 xx 轴)之间的角度称为极角(通常记作 θ)。
给定点的极坐标 (r,θ),可以转换为直角坐标 (x,y):
在极坐标下,二重积分的表达式为:
其中 r 和 θ 分别是极径和极角。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/140745.html







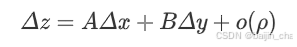





 ,并更新参数:
,并更新参数: 


