大家好,欢迎来到IT知识分享网。
Problem F: 凹凸四边形
Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 2322 Solved: 937
[Submit][Status]
Description
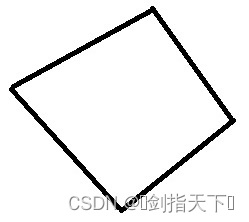
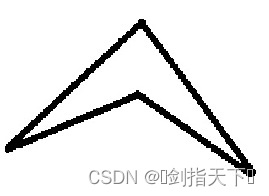
四边形分为凸四边形和凹四边形,如下图,左图为凸四边形,右图为凹四边形。
按照连边顺序给出四边形的四个顶点坐标,判断该四边形是凹四边形还是凸四边形。
Input
输入有多组测试用例。首先输入一个T(T<=100),表示测试用例数量。之后每组测试用例输入四行,每行输入两个整数(xi,yi)表示四边形顶点坐标。(-10000<=xi,yi<=10000,输入保证四个点一定能构成四边形)
Output
每组测试用例输出一行,如果是凸四边形,输出“convex”;否则,输出“concave”(不带引号)。
Sample Input
2
0 0
1 0
1 1
0 1
0 0
1 2
0 1
-1 2
Sample Output
Case 1: convex
Case 2: concave
HINT
向量有点乘(又叫内积)和叉乘(又叫叉积、外积)两种。
此题的一个解法是:用向量叉乘(又叫叉积、外积)判断欧式空间上的线段相交。算是线性代数在解析几何上的应用吧。
似乎从14级开始,线性代数课因减轻学生数学压力缩略课时,解析几何内容节省掉了。因此,向量乘法及其在几何上的应用敬请查书、百度、自学。
向量叉积的应用可以参考:向量叉积的运用 – 百度文库
当然,本题用其他方法也是可以做过的,因精度要求不高,如果精度要求高的话,向量叉积是最好的方法。
Append Code
解法如下:
#include <stdio.h> struct { int x[5]; int y[5]; double t[5]; } p; int main() { int num, i; scanf("%d", &num); for (i = 1; i <= num; i++) { scanf("%d %d", &p.x[1], &p.y[1]); scanf("%d %d", &p.x[2], &p.y[2]); scanf("%d %d", &p.x[3], &p.y[3]); scanf("%d %d", &p.x[4], &p.y[4]); p.t[1] = (p.x[4] - p.x[1]) * (p.y[2] - p.y[1]) - (p.y[4] - p.y[1]) * (p.x[2] - p.x[1]); p.t[2] = (p.x[1] - p.x[2]) * (p.y[3] - p.y[2]) - (p.y[1] - p.y[2]) * (p.x[3] - p.x[2]); p.t[3] = (p.x[2] - p.x[3]) * (p.y[4] - p.y[3]) - (p.y[2] - p.y[3]) * (p.x[4] - p.x[3]); p.t[4] = (p.x[3] - p.x[4]) * (p.y[1] - p.y[4]) - (p.y[3] - p.y[4]) * (p.x[1] - p.x[4]); if (p.t[1]*p.t[2]*p.t[3]*p.t[4] < 0.0001) printf("Case %d: concave\n", i); else printf("Case %d: convex\n", i); } return 0; }免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/141147.html