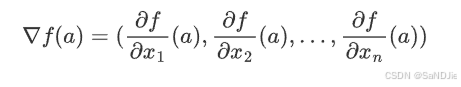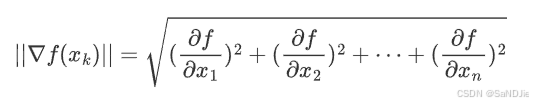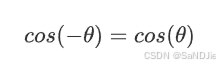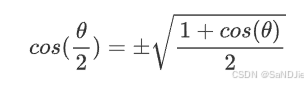2024.10.9高等数学学习笔记

大家好，欢迎来到IT知识分享网。

不定积分

1.定义

如果函数 F(x) 满足 F′(x)=f(x)，则称 F(x) 是 f(x) 的一个原函数。不定积分 $\int f(x)$

表示 f(x) 的所有原函数，通常写成： $\int f(x) dx=F(x)+C$

其中，C是积分常数，表示原函数的不确定性。 f(x)是被积函数，dx表示对 x 的积分变量。

不定积分的结果是一个函数簇，而不是一个具体的数值。其几何含义是一组平行的曲线簇。

2.基本积分公式

常数积分：

$\int k dx=kx+C$ (其中 k 是常数)

幂函数积分：

$\int x^{n} dx=\dfrac{x^{n+1}}{n+1}+C$ (其中 n≠−1)

指数函数积分：

$\int e^{x} dx=e^{x}+C$

$\int a^{x} dx=\dfrac{a^{x}}{ln a}+C$ (其中 a>0 且 a≠1)

对数函数积分：

$\int \frac{1}{x}dx=ln\left | x \right | + C$

三角函数积分：

$\int sinx dx= -cosx + C$

$\int cosx dx = sinx + C$

反三角函数积分：

3.换元积分法

3.1 第一类换元积分法

3.2 第二类换元积分法

第二类换元积分法通常涉及三角函数替换或带根号形式的替换。

定积分

定积分是微积分中的一个重要概念，用于求解函数在某个区间上的累积效应或面积。

$\int_{a}^{b}f(x)dx$ 表示函数 f(x)在区间 [a,b]上的累积效应或面积

定积分

$\int_{a}^{b}f(x) dx$

的几何意义是函数 f(x) 在区间 [a,b]上的曲线下面积。具体来说：

如果 f(x)≥0，则定积分表示曲线下方的面积。
如果 f(x)≤0，则定积分表示曲线上方的面积的负值。

3.性质

定积分具有以下重要性质：

线性性质：
其中 c 和 d 是常数。
区间可加性：
其中 a≤c≤b。
积分上下限交换：
定积分中值定理
如果函数 f(x) 在闭区间 [a,b] 上连续，则存在 c∈[a,b]，使得：

4.微积分基本公式

牛顿-莱布尼茨公式

5.定积分换元法

步骤

选择合适的变量替换：选择一个合适的变量替换 t=g(x)，使得积分变得更简单，并求反函数：

求导数：对 x 的导数

替换积分变量：将原积分中的 x 替换为 t，并将 dx 替换为

确定新的积分上下限：将原积分的上下限 a 和 b 替换为新的上下限 t 的值。即 t 的下限为 t1，上限为 t2。

求解新积分：求解新的定积分

多元函数

1.二元极限

定义

设函数 f(x,y) 在点 (a,b) 的某个去心邻域内有定义。如果对于任意给定的正数 ϵ，总存在正数 δ，使得当

时，总有：

∣f(x,y)−L∣<ϵ

则称 L 为函数 f(x,y)在点 (a,b)处的极限，记作：

几何意义

当点 (x,y)从任意方式趋近于点 (a,b) 时，函数 f(x,y) 的值趋近于 L。换句话说，函数图像在二维平面的点 (a,b)附近趋近于一个三维立体平面上的点 (a,b,L)。可将(a,b)想象为(a,b,L)投影在二维平面的点。

如果 (x,y)从不同方式趋近于点 (a,b)，函数 f(x,y) 的值不相等，则表示 f(x,y) 不存在。

2.偏导数

‌偏导数是‌多元函数求导的一种形式，表示在多个自变量中，当其中一个自变量改变而其他自变量保持不变时函数值的变化率。

这实质上是将其他自变量视为常数，然后按照单变量函数求导的方法进行运算。‌

定义

设函数 f(x,y) 在点 (x0,y0) 的某个邻域内有定义。如果极限：

存在，则称此极限为函数 f(x,y)在点 (x0,y0) 处对 x 的偏导数，记作：

类似地，如果极限：

存在，则称此极限为函数 f(x,y)在点 (x0,y0)处对 y的偏导数，记作：

‌偏导数的计算方法‌

对于二元函数z=f(x,y)，求z对x的偏导数时，将y看作常量，对x求导；求z对y的偏导数时，将x看作常量，对y求导。

3.全微分

定义

如果函数z=f(x, y)在点(x, y)处的全增量

可以表示为

，其中A、B不依赖于Δx, Δy，仅与x, y有关，ρ趋近于0(ρ=√[(Δx)²+(Δy)²])，此时称函数z=f(x, y)在点(x, y)处可微分，AΔx+BΔy称为函数z=f(x, y)在点(x, y)处的全微分，记为dz即dz=AΔx +BΔy。

可微的必要条件条件

若z=f(x,y)在(x,y)点处可微，则偏导数

存在，并且

可微的充分条件

z=f(x,y)在(x,y)的某个邻域内有连续的偏导数

则在(x,y)处可微，

4.梯度

梯度是一个向量，表示多元函数在某一点处的最大变化率和变化方向。

定义

设 f(x1,x2,…,xn)是一个定义在 Rn(n维欧几里得空间) 上的多元函数，函数 f在n维向量点 a=(a1,a2,…,an)处的梯度定义为：

其中，

是函数 f 在点 a 处对第 i 个自变量的偏导数。

性质

最大变化率：梯度 ∇f(a) 的方向是函数 f在点 a 处变化率最大的方向。
变化率：梯度 ∇f(a) 的大小（模）是函数 f 在点 a 处沿梯度方向的变化率。

沿梯度方向是是函数 f在点 a 处变化率增加最大的方向；沿梯度反方向是是函数 f在点 a 处变化率减小最大的方向；沿梯度垂直方向函数 f在点 a 处变化率为0。

梯度下降

梯度下降是一种优化算法，用于寻找多元函数的最小值。其基本思想是沿着函数的负梯度方向逐步更新参数，以减少函数值。

算法步骤

初始化：选择一个初始点 x0。
迭代更新：对于每次迭代 k，计算当前点的梯度

，并更新参数：

其中，η 是学习率（步长），控制每次更新的步幅。
终止条件：当梯度的模足够小或达到预设的迭代次数时，停止迭代。通常，终止条件可以是以下几种：
1. 梯度的模足够小：当梯度的模（或范数）
  
  小于某个阈值时，停止迭代。
  
  说明：
  
  梯度的范数表示梯度向量的大小，即梯度向量的长度。
  
  梯度的范数（模） ∥∇f(xk)∥是这个向量的欧几里得长度，定义为：
2. 达到预设的迭代次数：当迭代次数达到预设的最大迭代次数时，停止迭代。
3. 函数值变化足够小：当函数值的变化
  
  小于某个阈值时，停止迭代。

学习率

学习率 η是一个重要的超参数，控制着每次更新的步幅。选择合适的学习率对于梯度下降算法的性能至关重要：

学习率过大：如果步幅过大，算法可能会“跳过”最优解，导致在最优解附近来回震荡。
学习率过小：可能导致算法收敛速度过慢。

5.二重积分

二重积分是多元微积分中的一个重要概念，用于计算二维区域上的函数积分。它通常用于计算平面区域上的面积、质量、重心等问题。二重积分的基本思想是将一个二维区域分割成无数个小区域，然后在每个小区域上计算函数值的积分。

定义

设 f(x,y)f(x,y) 是定义在平面区域 D 上的函数，二重积分记作：

其中 dA表示面积元素。

几何意义

如果 f(x,y)是非负函数，二重积分

表示以 D 为底、以 f(x,y)为顶的曲顶柱体的体积。

二重积分的计算步骤-直角坐标系

在直角坐标系下，二重积分可以表示为两个定积分的乘积：

其中 D 是由 x=a 到 x=b 以及 y=g(x)到 y=h(x) 围成的区域。

确定积分区域 D：首先，你需要确定积分区域 D的边界。这个区域可以是矩形、圆形、多边形等。
设置积分限：根据积分区域 D，设置积分的限。例如，对于直角坐标系中的矩形区域，积分限通常是 a≤x≤b 和 c≤y≤d。
写出积分表达式：根据积分限写出二重积分的表达式：
计算内层积分：先对 y 进行积分，得到关于 x 的表达式。
计算外层积分：再对 x 进行积分，得到最终的积分值。

三角函数

1. 基本定义

正弦函数（sin）：
余弦函数（cos）：
正切函数（tan）：

2. 基本关系

2.1 毕达哥拉斯恒等式

这个恒等式可以从直角三角形的勾股定理推导出来。

2.2 商数关系

2.3 倒数关系

3. 三角函数的周期性

正弦函数和余弦函数：

其中，k 是任意整数。
正切函数：

其中，k 是任意整数。

4. 三角函数的对称性

正弦函数：
余弦函数：
正切函数：

5. 三角函数的和差公式

正弦函数的和差公式：
余弦函数的和差公式：
正切函数的和差公式：

6. 三角函数的倍角公式

正弦函数的倍角公式：
余弦函数的倍角公式：
正切函数的倍角公式：

7. 三角函数的半角公式

正弦函数的半角公式：
余弦函数的半角公式：
正切函数的半角公式：

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/141227.html