大家好，欢迎来到IT知识分享网。
漫谈二阶电路的零状态响应(初稿)
对于零输入响应(ZIR)，它的微分方程是不含常数项的，也叫齐次方程。 公式应该长成这样：
而对于零状态响应(ZSR)，它的微分方程是含常数项的，也叫非齐次方程。 公式长成这样:
鉴于上一篇文章描述不详细，公式存在缺漏，所以特地补充这篇文章 对于二阶非齐次微分方程，以下两种表达是一样的：
我们首先研究二阶电路的零状态响应。
我们先来看电路图：
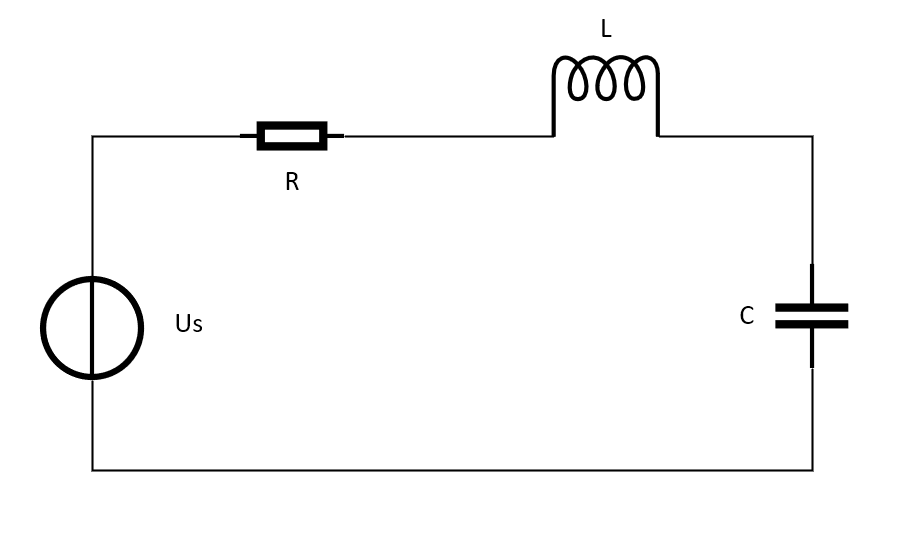
1. 由能量守恒得
因为，电感电压公式为
所以原式等于
又因为电容的电流为
因为串联电路，电流处处相等 所以原来的式子等于
化简得
我们得到这个最终方程，这个最终方程只有一个变量
,其他都为常量，这个方程和二阶非齐次微分方程是一样的。 也就是说，如果我们要解决RLC电路，那么我们要首先找出二阶非齐次微分方程的特解或者通解。
由于非齐次方程比较难求解，所以我们首先看二阶线性齐次方程：
观察这个式子，
我们首先构造几个式子
,
，为什么要这么构造呢？想必大家并不陌生，
求导的结果是它本身，引入
非常方便我们的计算，但是为什么要引入
呢？这种构造方法叫做微分算子。
在数学中，微分算子是定义为微分运算之函数的算子。首先在记号上，将微分考虑为一个抽象运算是有帮助的，它接收一个函数得到另一个函数。
二阶线性齐次微分方程：
那么将上式代入，可得
最终得到
此二次方程有两个解，
和
。 –
通解为
通解为
,
通解为
我们再回到RLC电路方程
把它变成二阶线性微分方程的标准形式
特征方程为
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/141310.html
