利用虚短和虚断分析基本的线性电路

大家好，欢迎来到IT知识分享网。

一，什么是虚短和虚断

虚短：在理想的运放电路中输入两端的电压无限接近，即V+=V-

虚断：输入端的电阻很高，等效于i+=i-

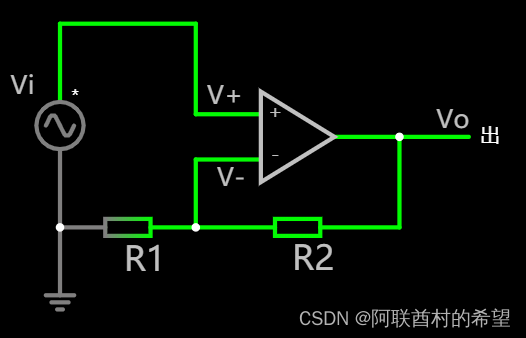
二，同相放大电路

根据理想运放的特性

V+ ≈ V- (虚短)

I+ = I- = 0 (虚断)

所以反向输入端没有电流，R1,R2串联分压

$Vi = V+ = V- =\frac{R1}{R1+R2}\cdot Vo$

电压增益 $Av=\frac{Vo}{Vi}=1+\frac{R2}{R1}$

由于虚短和虚断，Vi=V+，Ii = I+ ≈0

输入电阻 $Ri =\frac{Vi}{Ii} \rightarrow \infty$

输出电阻 $R_{o}\rightarrow 0$

三，电压跟随器

同相放大电路的一种特殊形式，根据同相放大电路的增益计算公式，Av=1；

Vo = V- = Vi ；I+ ≈ 0；所以Ri ≈ ∞

作用：隔离或缓冲，将负载和信号源之间隔离开，负载电阻变动，输出电压不跟随变动

四，反相放大电路

根据理想运放的特性

V+ ≈ V- (虚短)

I+ = I- = 0 (虚断)

所以 V+ ≈ V- = 0, I- = 0 ; 即 $I_{R1} =I_{R2}$

即 $\frac{Vi -V _{-}}{R1} =\frac{V _{-} -Vo}{R2}$

电压增益 $Av=\frac{Vo}{Vi}=-\frac{R2}{R1}$

输入电阻 $Ri =\frac{Vi}{I_{R1}} =\frac{Vi}{Vi/R_{1}} =R_{1}$ (实际电路中R1不能选择太大)

输出电阻 $R_{o}\rightarrow 0$

五，求差电路

方法一

Vi1接地，Vi2作用，是同相放大电路 $V_{o1}=\frac{Vo}{Vi}=\left ( 1+\frac{R4}{R1} \right )\cdot \frac{R2}{R2+R3}\cdot V_{i2}$

Vi2接地，Vi1作用，是反相放大电路 $V_{o2}= -\frac{R4}{R1}V_{i1}$

所以 $V_{o}=V_{o1}+V_{o2}=\left ( \frac{R1+R4}{R1} \right )\cdot \left ( \frac{R2}{R2+R3} \right )\cdot V_{i2}-\frac{R4}{R1}V_{i1}$

方法二

根据虚短，虚断和N,P点的KCL得

$V_{n}=V_{p}$ $\frac{V_{i1}-V_{n}}{R1} = \frac{V_{n}-V_{i1}}{R4}$ $\frac{V_{i2}-V_{p}}{R2} = \frac{V_{p}-0}{R3}$

即 $V_{o}=\left ( \frac{R1+R4}{R1} \right )\cdot \left ( \frac{R2}{R2+R3} \right )\cdot V_{i2}-\frac{R4}{R1}V_{i1}$

( $V_{i2}-V_{i1} =V_{id}$ 称差模输入电压)

当 $\frac{R_{4}}{R_{1}} = \frac{R_{3}}{R_{2}}$

(差模输入电压: $V_{i2}-V_{i1} =V_{id}$ )

$V_{o}=\frac{R4}{R1}\left ( V_{i2}-V_{i1} \right )$

差模电压增益 $A_{vd}=\frac{V_{o}}{V_{i2}-V_{i1}}=\frac{R4}{R1}$

（共模输入电压： $V_{i2}=V_{i1} =V_{ic}$ ）

由于虚短和虚断，此时 $I_{id}=I_{2} =I_{3}=-I_{1}=-I_{4}$

（省略）

差模输入电阻 $Ri =\frac{Vid}{I_{id}} =R_{1}+R_{2}$

此时输入电阻有限，要提高输入电阻，两个输入端加一个电压跟随器，此时电路的输入电阻无穷大，此电路为仪用放大器

若继续 $R_{4}=R_{1}$

则 $V_{o}=V_{i2}-V_{i1}$

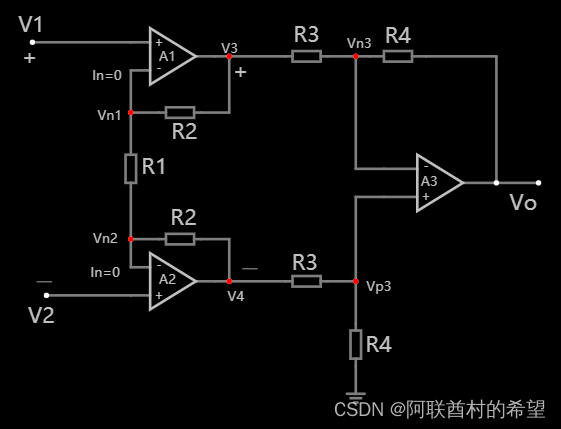
六，仪用放大器

由虚短得 $V_{R1}=V_{1}-V_{2}$

由虚断 $\frac{V_{3}-V_{4}}{2R_{2}+R_{1}}=\frac{V_{R1}}{R1}$

所以 $V_{o}=\frac{R4}{R3}\left ( V_{4}-V_{3} \right )=-\frac{R4}{R3}\left ( 1+\frac{2R_{2}}{R_{1}} \right )\left ( V_{1}-V_{2} \right )$

得电压增益 $Av=\frac{Vo}{V1-V2}=-\frac{R4}{R3}(1+\frac{2R_{2}}{R1})$

七，求和电路

方法一

Vi1接地，Vi2作用，是同相放大电路 $V_{o1}= -\frac{R3}{R2} V_{i2}$

Vi2接地，Vi1作用，是反相放大电路 $V_{o2}= -\frac{R3}{R1}V_{i1}$

所以 $-V_{o}=V_{o1}+V_{o2}=\frac{R3}{R1} V_{i1}+\frac{R3}{R2} V_{i2}$

方法二

根据虚断得

$I_{1}+I_{2}=I_{3}$

即 $\frac{V_{i1}-V_{n}}{R1}+\frac{V_{i2}-V_{n}}{R2} = \frac{V_{n}-V_{o}}{R3}$

根据虚地得

$V_{n}=0$

即 $-V_{o}=\frac{R3}{R1} V_{i1}+\frac{R3}{R2} V_{i2}$

此时输出反向，加一个反向放大电路即可消去负号

运放在反相端输入的时候，正相端（经过电阻）接地，导致U+＝U-＝0。

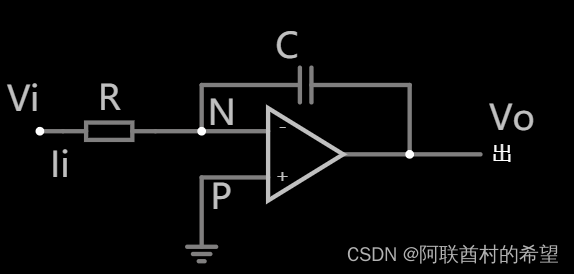
八，积分电路

(电容器上电压电流的关系 $V=\frac{1}{C}\int idt$ $i=C\frac{dV}{dt}$ )

根据虚短 Vn=0 所以 Vn – Vo =Vc

根据虚断 I-=0 Ic=Ii Ii=Vi/R

即 $V_{n}-V_{o}=\frac{1}{C}\int I_{i}dt=\frac{1}{C}\int \frac{V_{i}}{R}dt$

所以 $V_{o}=-\frac{1}{RC}\int V_{i}dt$

与一般RC电路有何区别（之后拿出来单独分析）

应用：函数发生器（三角波或锯齿波发生器），有源滤波器，显示器的扫描电路，模数转换器或作为数学模拟运算器等。

九，微分电路

推导方式与积分电路相似，可自行推导

$V_{o}=-RC\frac{dv_{i}}{dt}$

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/142034.html