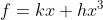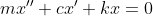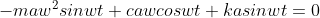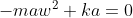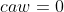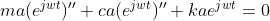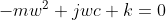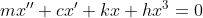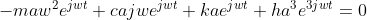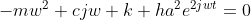非线性动力学 nonlinear dynamics

大家好，欢迎来到IT知识分享网。

参考：Friswell M I , Penny J , Garvey S D , et al. Dynamics of Rotating Machines. cambridge university press, 2010.

线性刚度、线性阻尼

只有小位移时
非线性弹簧可被线性化，kx
非线性库伦阻尼可被线性化，可等效为一个当量粘性阻尼，cx’

非线性刚度

现在考虑一个单自由度系统中，弹簧的位移与力的关系为非线性，
承受简谐激励力，计算稳态时的响应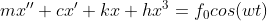？ Duffing equation

谐波平衡法

谐波平衡法将响应视为周期响应，所以响应可写作多个简谐函数的叠加，即傅里叶级数 $x=A_0+\sum A_nsin(nwt+\varphi _n)$ ，w为激励力的频率。
该方法只能求稳态解。

求解响应

谐波平衡法，假设响应为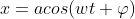 $x=acos(wt+\varphi )$ 式1
式2
将激励力改写如下
式3
将三个式子带入动力学方程得到两个方程，（关于cos为0与sin为0两个方程）
式4
式5
两个方程求平方再相加，消去Φ，得到一个方程
式6

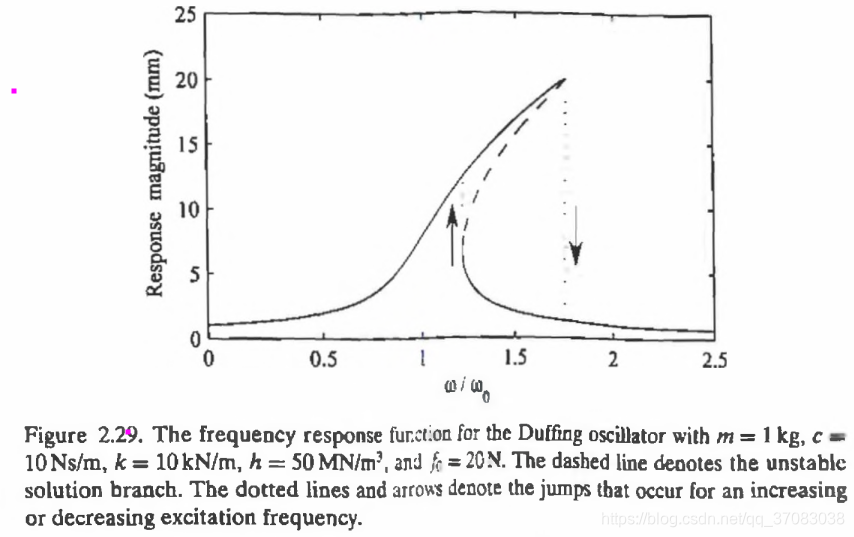
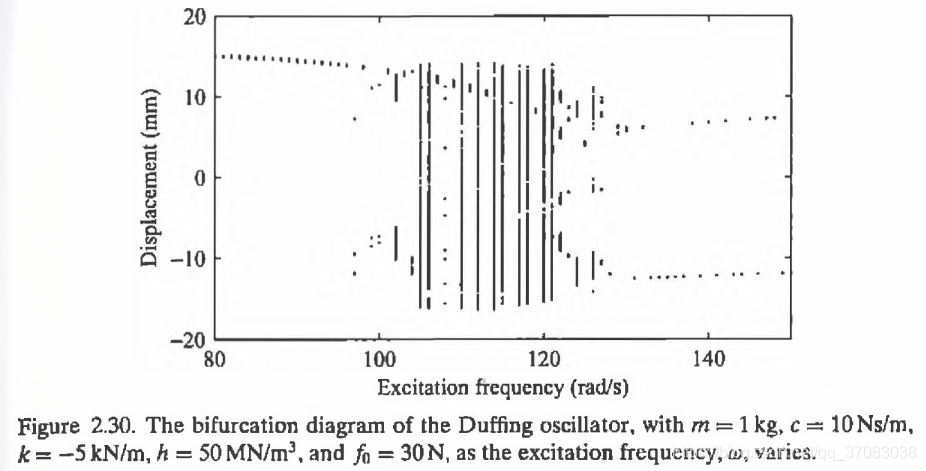
如图，在k m c h f0如此设置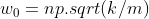，， w/w_0 为无量纲数，a随着w的变化。
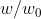
w由小到大，a增大到一点(1.75处)后突然跳变，逐渐减小。
w由大到小，a增大到一点(1.22处)后突然跳变，逐渐减小。
跳变表明系统发生了质变，跳变也称分叉。
其实这是书上这么写的，但我编程并没有发现如此。

import sympy as sp import numpy as np # 设定参数值 m = 1 # kg k = 10*10e3 # kN/m c = 10 # Ns/m h = 50*10e6 # MN/m3 M=10e6 f0 = 20 # N # a 为待求解 a = sp.symbols('a',real=True) # 只求实数 , real=True # 线性系统的固有频率 wn = np.sqrt(k/m) # a随w的变化 for k in np.arange(0,3,0.005): # 频率比 w = k*wn eq = (-m*w2+k+3/4*h*a2)2*a2+c2*w2*a2-f02 result = sp.solve(eq,a) result = np.array(result)*10e3 # m convert to mm result = np.unique(np.abs(result)) # 求模 去重 print(result)

工科学生不懂没事，不懂就学，说错也没事，知错就改，但要把明确的概念来作不明确的表达就是你的问题了。

固有频率

令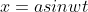，得

得到两个方程

caw=0
这个思路错了，但是如果按照三角公式应该也可以化简出来，最简便的就是直接设响应为复指数而不是简谐函数

令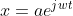 $x=ae^{jwt}$ ，得
$ma(e^{jwt})''+ca(e^{jwt})''+kae^{jwt}=0$
化简为

二元一次方程大家都会解了
注：我在求解固有频率时，未考虑响应的相位，这不影响求解固有频率

import sympy as sp m,c,k,w = sp.symbols('m,c,k,w') result = sp.solve(-m*w2+1j*w*c+k,w) print(result) # 注意： sympy结果 I 表示虚数

针对本问题求解固有频率

令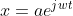 $x=ae^{jwt}$ ，得
$-maw^2e^{jwt}+cajwe^{jwt}+kae^{jwt}+ha^3e^{3jwt}=0$
得 $-mw^2+cjw+k+ha^2e^{2jwt}=0$
该非线性方程得到固有频率会随时间变化。

混沌

分岔图用来展示系统的非线性和混沌效应

激励力为简谐函数，频率w（角频率）
>129或<96时，响应为简谐函数，频率w
129>w>96时，如w=100，响应为周期函数，即复合的简谐函数，包括了基频与次倍频；如w=120，响应为非周期函数，是混沌的。
w=100
w=120

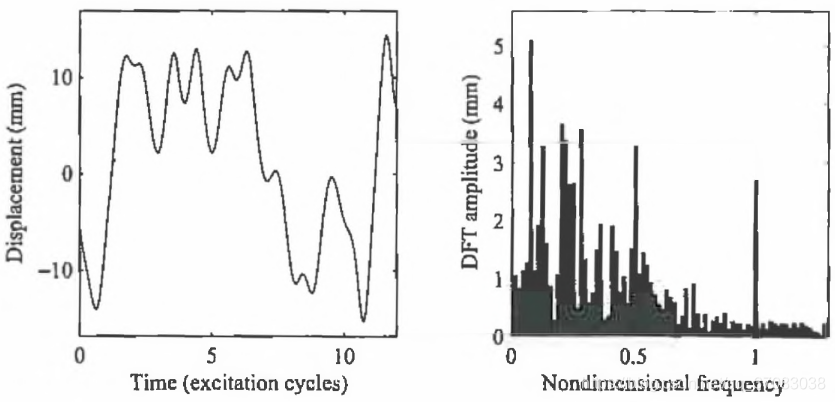
通过庞加莱图来分析w=120时的混沌效应
计算稳态位移与速度，注意：作图时，速度与位移采样率相同
如果是周期响应，庞加莱图绘制成的是一个固定形状。

非线性阻尼

$mx''+c(1-\gamma x^2)x'+kx=0$ Van der Pol equation
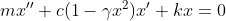
limit cycle：由于系统还有正阻尼，使得振动不会无限大，最终振动为一稳态振动。

菱形为初始条件，不论初始条件多少，最终稳态运动为limit sycle（实线圈）

术语

sub-harmonics 低阶
super-harmonics 高阶
chaotic混沌
harmonic-balance method谐波平衡法
trigonometric formulate三角公式
be truncated被截断
Duffing
bifurcation diagram分岔图
to name just three 仅举三个例子
Poincare map庞加莱图
quasiperiodic准周期
chaotic混沌
phase plane相平面
self—excited system自激系统

庞加莱被公认是19世纪后和20世纪初的领袖数学家，是继高斯之后对于数学及其应用具有全面知识的最后数学家。

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/142849.html