丘成桐证明卡拉比猜想错误百出

大家好，欢迎来到IT知识分享网。

                                                                  王晓明

一，缘起

1954年的国际数学家大会上，31岁的意大利裔数学家卡拉比，在会议的邀请报告中用一页纸写下了他著名的猜想：令M为紧致的卡勒（Kahler）流形，那么对其第一陈类中的任何一个（1，1）形式R，都存在唯一的一个卡勒度量，其Ricci形式恰好是R。

丘成桐解释说：

1，卡拉比猜想实际上与蒙日-安培方程等价。

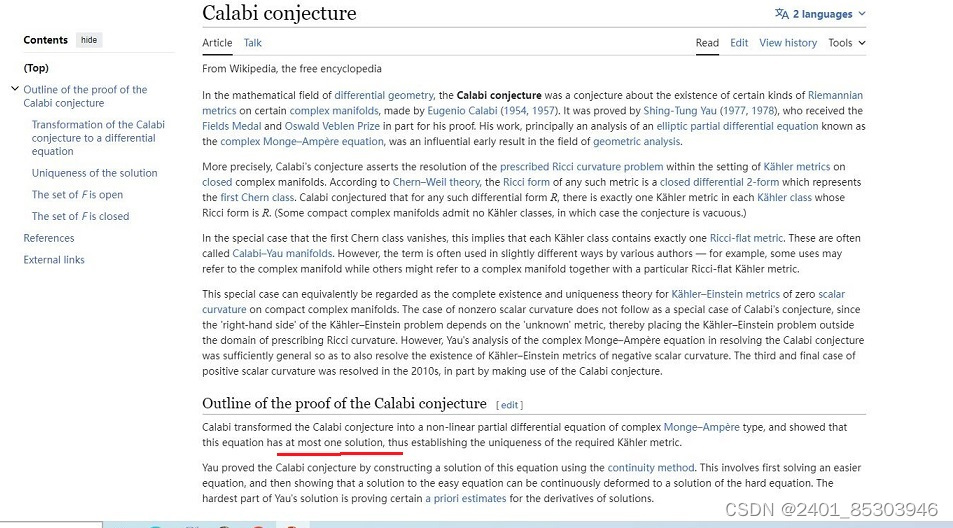
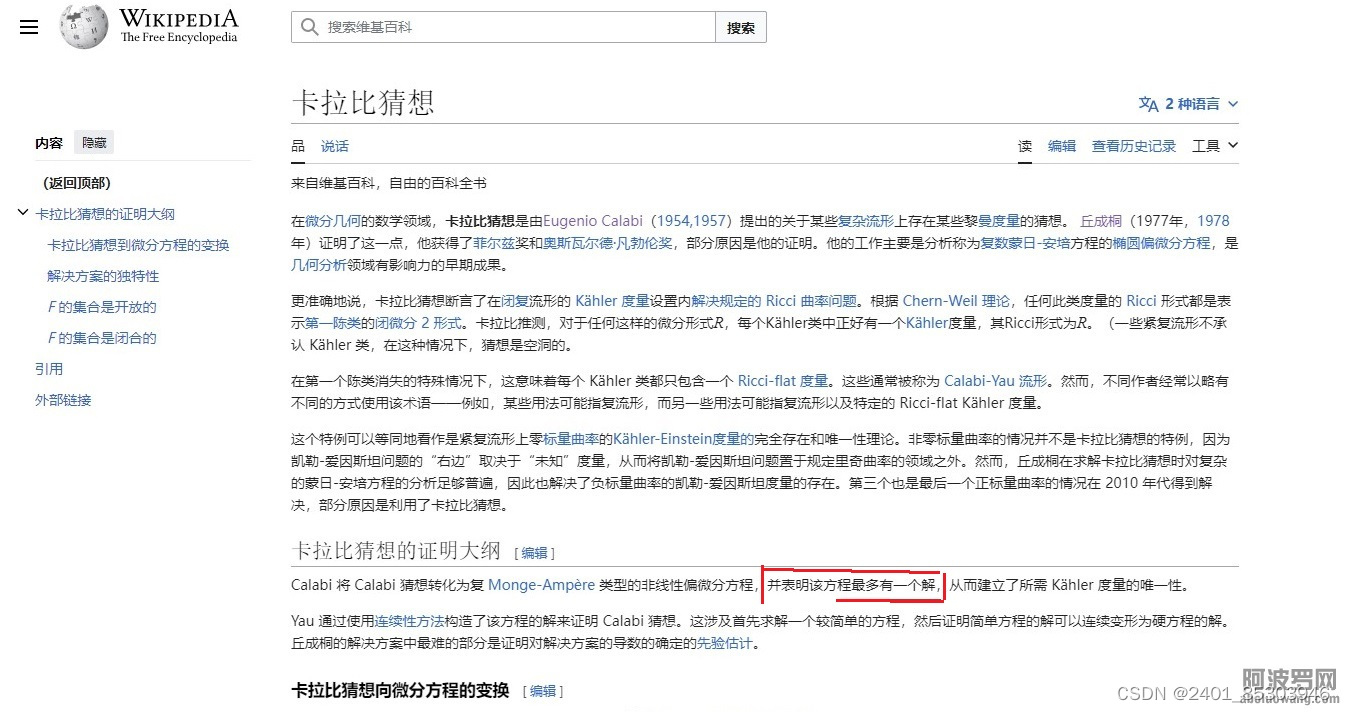
2，要求解的这个蒙日-安培方程，是一个很难的非线性偏微分方程。他花了将近3年时间，做了大量准备工作，发展了强有力的偏微分方程技巧，使用先验估计方法，在1976年6月求解了这个非线性复蒙日-安培方程（至多有一个解）。

3，从而给出了卡拉比猜想的证明（实际上是：丘成桐证明了其流形上复数的蒙日—安培方程，至多只有一个解。

二，驳斥丘成桐荒谬结论

丘成桐说的【至多有一个解】的含义是：

1，否定至少有两个或者两个以上的解，最多一个解（上限）。

2，不能保证有一个解。很可能一个解也没有（下限）。

就是说，如果没有一个解的情况下，就不能说丘成桐解开了蒙日-安培方程。

为什么？因为，【至多只有一个解】属于或然性推理。或然性推理的前提与结论之间没有蕴含关系，所以，或然性推理的结论是不可靠的，大多数情况下是错误的。

数学定理必须是必然推理的判断。

3，丘成桐与卡拉比循环论证。

循环论证指：a，论据的正确性依赖于论题。b，两个论据之间互相依赖。

卡拉比说自己证明了唯一性，其中唯一性依赖于丘成桐的存在性；

丘成桐说自己证明了存在性，但是存在与否依赖于卡拉比的唯一性。

如果卡拉比的唯一性是真实的，那么，存在性就是真实的。典型的循环论证。

附1：1989年，田刚利用他先前引进的不变量以及他发展的部分连续模估计，彻底解决了复曲面上的Calabi问题。田刚首先给出例子说明，即使没有非零全纯向量场也有可能不存在Kähler- Einstein度量。

估计一词是或然判断，不能在数学证明中使用。

附2，摘录：

Yau  Calabi’s conjecture and some new results in algebraic geometry

我们将会看到，0″>

的情况要复杂得多：一般来说，无法保证KE度量的存在性和唯一性。